Использование статистических вычислений в биологии



В статье авторы определяют связи статистики и биологии.

Ключевые слова: математика, статистика, теория вероятности, биология.

Мы очень много говорим о межпредметных связях в обучении. Этому посвящены целые разделы в книгах на педагогическую тематику. И действительно без методологической функции межпредметных связей сформировать диалектико-материалистические взгляды на природу будет невозможно. И если вы думаете, что больше не о чем говорить на эту тему, то вы очень ошибаетесь.

Казалось бы, где математика, а где биология?! Хотя в современном образовательном цикле их относят в один естественно-математический раздел достаточно часто. Так вот самое примитивное в математике — это обычный счет или подсчет. Биологи, как в детской сказке царь Еремей, обязательно считают количество особей разных видов. Считают по разным признакам: по половой принадлежности, учитывают возрастные когорты, смотрят на рождаемость или смертность, сравнивают показатели веса или роста живых организмов и т. д. Казалось бы — где тут может быть сложная математика, когда идет обычный подсчет?

Но в математике есть разные разделы. Один из них ввели в школьные программы совсем недавно — это раздел «Вероятность и Статистика» — и это та отрасль, которая имеет большое прикладное значение. Благодаря этому предмету учащиеся познакомятся с формами представления и описания данных в статистике, случайным событиям, вероятностью и ее свойствами. И примеры можно черпать их разных дисциплин, в том числе и биологии. И это не случайно. Ведь математически-статистические методы в биологию пришли очень давно. Еще Ф.Гальтон в 1889 году ввел термин «биометрия» — что, по сути, и означает такие биологические исследования, которые используют познания в статистике [2, c.5].

Рассмотрим несколько примеров применения знаний из раздела «Теория вероятностей» в биологии. В 7 классе на уроках математики дети знакомятся со случайными величинами, учатся вычислять среднее арифметическое, медиану, размах, находить наибольшее и наименьшее значение [1, c.14]. Все эти знания они могут применить на уроках биологии при выполнении лабораторной работы «Изучение изменчивости. Построение вариационной кривой».

Целью работы является ознакомление с закономерностями модификационной изменчивости, методикой построения вариационного ряда и вариационной кривой. В ходе работы учащиеся измеряют листья одного растения, записывают данные.

Считают количество исследуемых объектов с одинаковыми показателями длины: 8 мм — 5 шт, 9 мм — 7 шт и т. д. Данные можно представлять в виде таблицы 1 или рисунка 1.

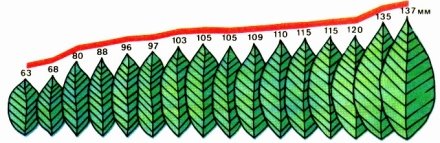
Рис. 1. Первый способ представления результатов

Таблица 1

Второй способ представления результатов

№ объекта	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Длина листа (фасоли) в см.

Далее учащиеся строят вариационный ряд и вариационную кривую, расположив семена в порядке возрастания длины объекта. На оси абсцисс откладывают значения отдельных величин — длину исследуемого объекта, а по оси ординат — значения, соответствующие частоте встречаемости данного исследуемого объекта. Результаты работы оформляются в виде графика, изображенного на рисунке 2.

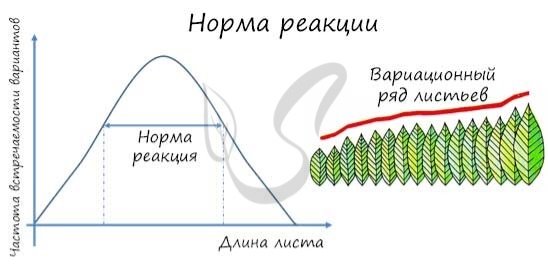
Рис. 2. Результаты лабораторной работы

Кроме этого, вычисляют среднюю величину признака по формуле:

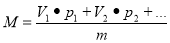
М — средняя величина, V — варианта (длина),

p — частота встречаемости (число исследуемого объекта),

m — общее число измерений.

В конце работы делают выводы и отвечают на вопросы, используя знания, полученные на уроках математики.

Рассмотрим еще один пример: применение темы «Распределение Пуассона» (11 класс, Теория вероятности и статистика) в биологии [2, c. 27].

Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Распределение Пуассона значительно отличается своей «предметной» областью: в нём рассматривается интенсивность событий. При большом значении числа испытаний удобнее всего использовать формулу Пуассона. Данная формула определяется теоремой Пуассона.

Теорема гласит, что если вероятность наступления события A в каждом испытании постоянна и мала, а число независимых испытаний достаточно велико, то вероятность наступления события A ровно раз приближенно равна:

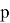
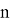
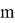
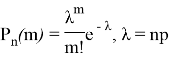
В качестве примера, мы можем рассмотреть задачу по статистике из курса биологии 11 класс: некоторое насекомое откладывает случайное число яиц , распределенное по закону Пуассона . Через некоторое время каждое яйцо независимо от других превращается в личинку с вероятностью . Пусть — количество появившихся личинок. Найдите вероятность и среднюю численность потомства.

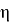
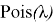
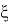
Решение: если бы количество отложенных яиц не было случайной величиной , а фиксированным числом , то можно было бы легко установить распределение потомства. В связи с этим рассчитаем условную вероятность .

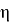
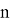
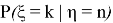
Поскольку превращение отдельного яйца в личинку можно описать одним экспериментом схемы Бернулли, то

, при . Среднее число личинок , поскольку это математическое ожидание биномиальной случайной величины. Условное математическое ожидание . По формуле полной вероятности для условных математических ожиданий находим: , где использовался тот факт, что математическое ожидание пуассоновской случайной величины равно значению параметра .

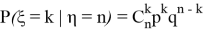
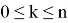
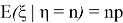
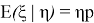
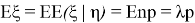
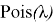
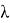
Распределение также находится по формуле полной вероятности , так что случайная величина имеет распределение Пуассона с параметром .

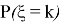
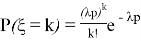
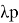
Таким образом, статистика и биология тесно взаимосвязаны друг с другом. Статистика является неотъемлемой частью биологических исследований, позволяя ученым делать объективные выводы на основе данных и повышать эффективность и точность научных исследований в биологической области.

Литература:

1. Зверев А. А., Зефиров Т. Л. Статистические методы в биологии: учебно-методическое пособие — Казань, КФУ, 2013–42 с.
2. Кожевников С. П. Алгоритмы биологической статистики — Ижевск: изд. центр «Удмуртский университет», 2018. — 75с.
3. Сыса А. Г., Живицкая Е. П. Статистический анализ в биологии и медицине — Минск: ИВЦ Минфина, 2018–140 с.