В последнее время, при проектировании зданий повышенной этажности необходимо определять НДС их несущей системы, с учетом последовательности возведения. Таким образом, возникает вопрос: какова основная причина неадекватности, при учете последовательности возведения, традиционных расчетных моделей.
Ключевые слова: ригель, традиционная расчетная модель, напряженно-деформированного состояния конструкций.
Recently, when designing high-rise buildings, it is necessary to determine the VAT of their bearing system, taking into account the sequence of construction. Thus, the question arises: what is the main reason for the inadequacy, taking into account the sequence of construction, of traditional calculation models.
Keywords: rigel, the traditional calculation model, stress-strain state of structures.
Для ответа на этот вопрос, проанализируем работу, рассмотренной выше двухпролетной рамы, однако модифицируем ее, как показано на рис. 1. При расчете по традиционной расчетной модели (а) ригели получают одинаковые прогибы, так как при одинаковой нагрузке и одинаковой их из-за гибной жесткости они деформируются одновременно и независимо друг от друга.
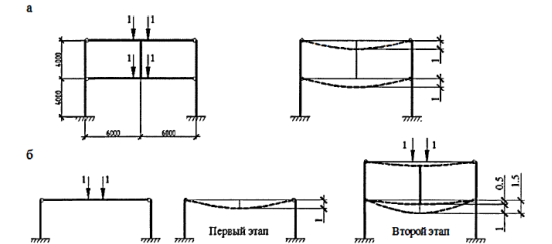
Рис. 1. Расчетные модели рамы. а — при одновременном загружении всех этажей; б — при последовательном загружении
При расчете по схеме, учитывающей последовательность возведения (Рис. 2), первый ригель на первом этапе нагружения деформируется аналогично ригелям первой расчетной модели, т. е. величина его прогиба также будет равна единице.
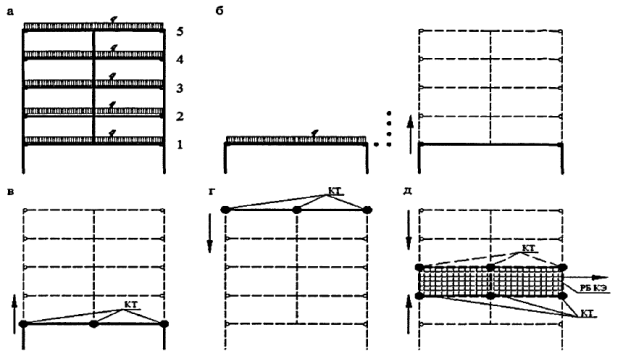
Рис. 2. Расчетные схемы пятиэтажной рамы. а — при одновременном загружении всех этажей; б — схема расчетной модели по предлагаемой методике ССЭ; в — схема скольжения ≪снизу вверх≫; г — схема скольжения ≪сверху вниз≫; д — схема встречного скольжения для определения деформированного состояния требуемого расчетного блока конечных элементов (РБ КЭ)
На втором этапе, когда загружен второй этаж, через среднюю стойку произойдет дополнительное нагружение нижерасположенного ригеля, при этом величина прогиба первого ригеля будет определяться как сумма его прогибов от первого и второго этапов нагружения. При этом легко заметить, что величина суммарного прогиба ригеля первого этажа подчиняется следующему ряду
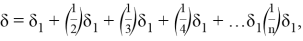
где
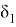
n — количество этажей над рассматриваемым ригелем.
Таким образом, согласно формуле (1), величина прогиба первого ригеля для двухэтажной рамы будет равна 1,5 <5 т. е. в 1,5 раза больше величины ее прогиба, получаемого по традиционной расчетной модели. По мере увеличения этажности рамы нагрузка неограниченно возрастает, так как ряд (1) является расходящимся.
В традиционной расчетной схеме, за счет одновременного приложения нагрузки на ригель, эффекта перенапряжения первого ригеля не наблюдается, так как при одинаковой жесткости ригелей и одинаковой нагрузке на них дополнительные усилия через стойку не передаются. Таким образом, при учете последовательности возведения необходимо учитывать начальную деформированность системы, которая отсутствует в традиционной модели. Следовательно, отрицание начального напряженно-деформированного состояния конструкций, при расчете по традиционной расчетной модели является одним из основных ее недостатков. Данный недостаток можно исправить включением в основную расчетную модель «передающих усилий», т. е. тех усилий, которые возникают в элементах схемы, учитывающий монтаж, например, в данном случае это будет продольная сила в стойке, имеющая противоположное направление. Подставив данное усилие в первую расчетную модель, можно заметить, что величина деформаций ригеля будет такой же, как и в модели, учитывающей монтаж. Однако следует отметить, что такой подход требует нескольких действий. Например, в данном случае, необходимо, во-первых, определить «передающие» усилия, путем приложения нагрузки только к вышерасположенному этажу. Во-вторых, внести в традиционную модель полученные величины, путем придания «фиктивного» предварительного напряжения, средней стойке рамы. Таким образом, только после указанных выше операций, традиционная модель получится адекватной «монтажной» модели.
Очевидно, что такой ход постепенного расчета и изменения традиционной схемы имеет один большой недостаток, а именно значительно увеличивается время и трудоемкость расчета, поскольку приходится создавать множество расчетных схем, результаты которых, должны быть «подставлены» в традиционную модель. При этом повышается вероятность ошибки, которая может возникнуть на одном из этапов, однако будет не замечена или упущена, что в свою очередь повлияет на правильность конечного результата и в итоге на качественную и количественную оценку всего НДС исследуемого объекта.
Для исследования вопроса необходимости учета последовательности возведения, в многоэтажных зданиях, рассмотрим туже самую раму, однако количество этажей увеличим с двух до девяти рис. 3.
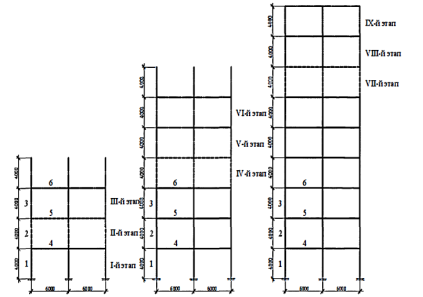
Рис. 3. Расчетная модель многоэтажного здания, с учетом последовательности возведения
На основании расчета построим графики изменения изгибающих моментов в крайней колонне в элементах 1,2,3, и в ригелях в элементах 2,3,4 по мере возведения этажей каркаса, рис.4.
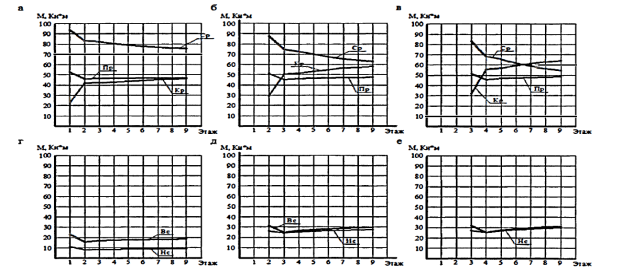
Рис. 4. Графики изменения изгибающих моментов в ригелях (а, б, в) и колонне (г, д, е) соответственно первого, второго и третьего этажей, в зависимости от этажности каркаса Кр — усилие на крайней левой опоре ригелея, Пр — усилие в пролете ригеля, Ср — усилие на средней опоре ригеля, Вс — усилие в верхнем сечении колонны, Нс — усилие в нижнем сечении колонны
Отметим, что точка на графике для 9-го этажа (IX-й этап нагружения) соответствует также одновременной схеме нагружения, а именно расчетной модели традиционного подхода.
На графиках, описывающих изменение изгибающего момента в ригеле (рис 4 а, б, в), отчетливо видно, что величина момента в пролете ригеля не существенно изменяется, по сравнению со схемой, учитывающей монтаж.
Аналогично изменению пролетного момента, изменяются и величины изгибающих моментов в сечениях крайних колонн (рис. 4 в, г, д).
Учитывая, что с ростом этажности возрастает продольное усилие в колоннах, которое становится определяющим при их конструировании, то можно сделать вывод о неактуальности учета последовательности возведения при расчете колонн многоэтажных, и в особенности высотных зданий.
Изменение изгибающего момента на крайней опоре в ригеле (рис. 4 а, б, в), линия Кр, также не является опасным, поскольку можно заметить, что с ростом этажности напряжения увеличиваются, достигая максимума расчетной схемы возведенного здания (IX-й этап нагружения), т. е. при традиционной расчетной модели, которая является для большинства зданий основной расчетной. Что объясняется увеличением жесткости узла. Таким образом, учет последовательности возведения для крайних опор ригеля не актуален, так как не наблюдается уменьшение прочности сечения ригеля.
Наиболее интересным является характер изменения величины изгибающего момента на средней опоре, линия Ср (см. рис. 4 а, б, в). Отчетливо видно, что с ростом этажности величины моментов уменьшаются, достигая минимума при традиционной схеме. Только в данном случае величина изгибающего момента, полученного по схеме, учитывающей монтаж, более чем в 1,5 раза превосходит значения, получаемые по традиционной схеме. Объясняется это тем, что крайняя опора при отсутствии вышерасположенных ригелей на стадии возведения, поворачивается значительно сильнее, чем при их наличии, что объясняется более низкой жесткостью рассматриваемого узла.
На основании вышесказанного, можно сделать вывод, что с ростом этажности происходит перераспределение усилий, вызванное дополнительными деформациями нового этажа. При этом с добавлением одного этажа происходит уменьшения угла поворота в первоначальной схеме, при добавлении следующего этажа наблюдается разгрузка первого добавленного этажа, однако первоначальный этаж, наоборот, догружается. Таким образом, каждый нечетный добавленный этаж (1,3,5...) разгружает рассматриваемый, а четный (2,4,6...) наоборот догружает. Учитывая, что при повороте узла момент на противоположном конце ригеля в два раза меньше, чем момент в поворачиваемом, изменение изгибающего момента, обусловленное поворотом крайнего узла сопряжения ригеля с колонной, подчинено следующему числовому знакопеременному ряду:
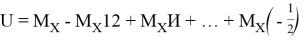
где, М х — изгибающий момент в рассматриваемом ригеле, возникающий при добавлении одного этажа.
Предположим, что величина изгибающего момента в пролете ригеля, при отсутствии вышележащих ригелей, всегда больше величины, получаемой при их наличии.
Обозначим величину пролетного момента в ригеле как Л/пр. По мере возведения этажей опорный момент будет изменяться на некоторую величину M h . Используя ряд (2), определим его сумму. Данный ряд, согласно признаку сходимости знакочередующегося ряда (признаку Лейбница), является абсолютно сходящимся, при этом сумма данного ряда будет равняться (3):
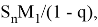
Получившееся число положительное, соответствует разгружающему изгибающему моменту, следовательно, максимально возможный пролетный момент в ригеле, получаемый при наличии вышерасположенных ригелей, будет меньше получаемой, при их отсутствии на величину 2/3 М 1 . Следовательно, предположение верно. Данным фактом объясняется также и изменение величины опорного момента на опорах ригеля и в колонне.
Литература:
1. Дроздов П. Ф., Додонов М. И., Паньшин Л. Л., Р. Л. Саруханян. Проектирование и расчет многоэтажных гражданских зданий и их элементов. — М.: Стройиздат, 1986.-351с.
2. Динамический расчет зданий и сооружений / под ред. Б. Г. Корнеева, И. М. Рабиновича. — М.: Стройиздат, 1984. — 303с.
3. Дыховичный Ю. А. Конструирование и расчет жилых и общественных зданий повышенной этажности. — М.: Строй-издат, 1970. — 248с.
4. Белостоцкий А. М. Комплексное расчетное обоснование напряженно- деформированного состояния высотных многофункциональных комплексов /А. М. Белостоцкий, Д. К. Каличаева [и др.] // Стр. мех. и расч. соор., 2006. — № 6. — С.52–56.







