Статья анализирует важность изучения тождественных преобразований в алгебре, особенности и трудности этого процесса на различных этапах школьного обучения.
Ключевые слова: тождественные преобразования, этапы изучения, типичные ошибки.
Линия тождественных преобразований является одной из основных в алгебре и занимает значительную часть учебного времени в курсе школьной математики. Обеспечение высокой культуры тождественных преобразований представляет актуальную проблему обучения математике, поскольку ежегодно при проверке контрольных и самостоятельных работ, учителя отмечают ошибки и нерациональные приёмы вычислений и преобразований, допускаемых обучающимися различных классов.
Школьная алгебра состоит из четырёх основных разделов: «Числа и вычисления», «Алгебраические выражения», «Уравнения и неравенства» и «Функции» и каждую из них пронизывают тождественные преобразования, что говорит о неоспоримой значимости изучения данной темы.
Изучение методической литературы и школьных учебников позволило выделить основные типы тождественных преобразований, применимых в основной школе:
— законы сложения и умножения;
— свойства вычитания;
— особые случаи действий (сложение и вычитание нуля и единицы);
— свойства дробей;
— свойства степеней;
— формулы сокращённого умножения;
— свойства корней.
Применение преобразований в математике можно подразделить на 4 основных этапа [3]:
1) Пропедевтический — строится на основе знаний свойств арифметических действий, например, для приведения подобных слагаемых применяют распределительное свойство, методу группировки предшествует ассоциативное свойство, а правила действий над числами задают порядок выполнения преобразований над буквенно-числовым выражением с целью его упрощения.
2) Начала алгебры — на этом этапе важно работать как со словесными формулировками правил и свойств, так и с их буквенными представлениями, научить анализировать выражения, видеть их как составляющие формулы.
3) Формирование навыков применения конкретных видов преобразований. Важное замечание для этого этапа — расширение понятия тождества в связи с появлением области допустимых значений.
4) Организация целостной системы преобразований (синтез) — переход к нему осуществляется при итоговом повторении курса, он характерен для 10–11 класса.
Все этапы взаимосвязаны между собой, но без должного усвоения хотя бы одного из первых трёх невозможно говорить об успешном изучении данной темы на четвёртом этапе. Сформулируем некоторые типичные ошибки, характерные для каждого из них.
Ещё на пропедевтическом этапе при переходе от числовых выражений к буквенным у обучающихся могут возникнуть некоторые трудности в непонимании факта того, что за переменной могут стоять различные числовые значения. Здесь можно использовать три пути мотивировки введения буквенной символики [1]:
— запись в символической форме различных предложений;
— вывод общих формул решения задач;
— составление и решение простейших уравнений.
Наиболее поучительным является третий путь, поскольку дети быстро оценивают решение задач алгебраическим методом и отрабатывают навык его применения.
На этапе начал алгебры при изучении преобразований целых алгебраических выражений может возникнуть несколько затруднений, связанных с непониманием смысла буквенных выражений и незнании действий с ними. Необходимо, чтобы учащиеся более ясно уяснили приведение подобных членов и действия над алгебраическими выражениями и выработали чёткие навыки грамотных простейших преобразований, исключая в последующем такие грубые ошибки, как:
1) отсутствие умножения на буквенную часть(
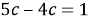
2) вычитание выражений с разной буквенной частью (
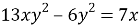
3) вычитание выражений, содержащих основание с разными показателями, незнание свойств степеней (
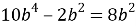
Изучение алгебраических дробей и действий с ними вызывает массовое допущение ошибок. В случае сомнений в том или ином преобразовании алгебраической дроби обучающиеся на первых порах могут обращаться к проверке на числовых значениях переменных и руководствоваться в решении результатами частного случая. Обилие практического материала обеспечит развитие навыка совершения преобразований над алгебраическими дробями, которые должны производиться уверенно и без предварительной проверки на частных примерах [2].
«Арифметический корень и его свойства» также является непростой для понимания школьников темой. В качестве основной ошибки можно выделить приравнивание правила «корень произведения равен произведению корней, входящих в него множителей» к умножению, делению и вычитанию корней:
1)
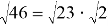
2)
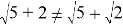
3)
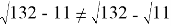
4)
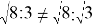
Представленные выше выражения, за исключение первого, не являются верными. Во избежание таких ошибок на первых этапах можно продемонстрировать неравенство обеих сторон, используя извлекаемые по таблице квадратов корни, например,
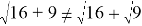
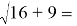
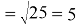
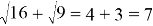
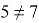
Таким образом, можно сделать вывод о том, что изучение тождественных преобразований непростая с методической точки зрения тема, которая имеет множество особенностей и имеет важное значении в целом при изучении алгебры основной школы.
Литература:
- Брадис, В. М. Методика преподавания математики в средней школе — Москва: Государственное учебно-педагогические издательство Министерства Просвещения РСФСР., 1954. — 495 c. — Текст: непосредственный.
- Бронштейн, С. С. Методика алгебры — Москва: Учпедгиз, 1935. — 329 c. — Текст: непосредственный.
- Петрова, Е. С. Теория и методика обучения математике — Саратов: Изд-во Сарат. ун-та, 2005. — 104 c. — Текст: непосредственный.







