Развитие логического мышления на уроках математики в 5–6-х классах



В статье рассматривается развитие логического мышления на уроках математики, методы и применение развивающих задач на практике. Логические задачи как средство формирования у обучающихся навыков логического мышления у обучающихся 5–6 классов.

Ключевые слова: обучающийся, логика, мышление, педагог, учитель, логические задачи.

Не мыслям надобно учить, а учить мыслить.

Э. Кант

Математика — увлекательная наука, успех в которой зависит от интереса. Главное — найти правильный подход и использовать потенциал этой науки для гармоничного развития личности ребенка.

Математика играет ключевую роль в развитии когнитивных способностей учащихся. На уроках математики, обучающиеся не только усваивают специфические знания и математические понятия, но и развивают мышление, память и внимание. Такие психические функции и процессы являются основой для решения проблем и анализа информации, что полезно во всех областях знаний и в повседневной жизни. Математика требует от учащихся активного участия и постоянной практики, что способствует улучшению их способности к абстрактному мышлению, логическому рассуждению и критическому анализу. Хотя каждый урок развивает логическое мышление, ребята часто не умеют делать обобщений, выводов, классификаций. Одной из первоочередных и важнейших задач школьного курса математики является задача развития логического мышления учащихся. В возрасте 11–12 лет, для эффективного решения задач, ученикам необходимо ясно осознавать и визуализировать описываемые в них сценарии. Успех в обучении требует от подростков умения глубоко анализировать, выделять суть, проводить сравнения, рассуждать логически, формулировать умозаключения и обосновывать их. Важно, чтобы они точно понимали, что служит причиной того или иного события, а что является его следствием. Для подростков характерно заметное развитие критичности мышления. Помимо авторитета преподавателя и учебника обучающийся хочет убедиться в справедливости той или иной своей мысли, того или иного положения, суждения. Также целесообразно стимулировать творческое мышление подростков, чаще ставить их перед необходимостью самостоятельно сравнивать различные объекты, находить в них сходство и различия, делать обобщения и выводы. Настоящее самостоятельное мышление у школьников развивается, когда они сталкиваются с проблемой или вопросом. Обязанность учителя заключается в том, чтобы снабдить учеников необходимыми принципами и особенностями для правильного познавательного процесса. Для развития логического мышления необходима постановка перед учениками учебной задачи, требующей от них нового анализа ситуации действия, нового ее понимания. Учителю следует сосредоточить свои усилия на том, чтобы управлять процессом решения задачи, стимулируя активное исследование и понимание её сути учениками. Важно, чтобы преподаватель вовлекался в этот процесс как равноправный участник, способствующий совместному поиску ответов, а не диктовал единственно верное решение. Когда участники вместе стремятся понять суть предстоящих задач, это превращает процесс в диалог: обучающиеся делятся своими идеями о теме, эмоциями, которые она вызывает, и своими оценками по поводу предмета обсуждения. В процессе совместной работы над задачами одновременно происходит развитие ключевых коммуникативных навыков: формируется способность к обоснованному выражению собственных идей и к внимательному и понимающему восприятию идей других, что способствует укреплению и развитию логического мышления.

На мой взгляд, наиболее целесообразно особое внимание уделять логической подготовке в курсе математики начиная с 5 класса, поскольку сам курс 5–6 классов требует более развитых логических умений. Анализ учебников выявил, что практически во всех учебниках курса математики 5–6 классов присутствует логический компонент. Учебники нацелены на развитие логического мышления и творческих способностей ребенка. Но поисковые, математические задачи, решение которых как раз и развивает логическое мышление, расположены в учебнике под заголовками «Для тех, кому интересно» (учебник для 5-х классов по математике Г. В. Дорофеева, И. Ф. Шарыгина, С. Б. Суворова, Л. Г. Петерсона).

Какие же способы существуют для развития логики? Развивать и тренировать логику и мышление можно и нужно разными способами.

1. Устные игры. Игры со словами помогают развивать логическое мышление, расширять кругозор и увеличивать словарный запас. Лучше выбирать игры, которые учат выделять аналогии, обобщать, распределять предметы и явления по группам, проводить логические связи. Играйте в ассоциации.

Например, ассоциации.

1. Не путать понятие число и цифра. Цифры используют для записи чисел так же, как буквы — для записи слов. Иногда цифра носит роль числа так же, как буква — роль слова. Например, буква (слово) Я или цифра (число) 7.

2. «Говорящие приставки». Например, для изучения единиц измерения.

Кило = 1000 1 кг=1000 г кило грамм; 1 км=1000 м кило метр

Санти = 1 м=100 см санти метр

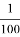
3. Периметр (от латинского «Пери» — вокруг); треугольник — ТРИ угла, вершины.

Окружность — ассоциация кольцо, круг — монета, эллипс — овал, шар — мяч.

2. Игры с картинками, образами. На таких занятиях можно пользоваться карточками, бумагой и ручками, которые стимулируют развитие образно-логического мышления. Например, игры на сравнение и группировку предметов по цвету, форме, размеру и другим признакам; головоломки со спичками; ребусы и головоломки на бумаге, проходите лабиринты.

Например, задача со спичками.

Составляем числа из спичек. Цифры от 0 до 9 составляем так, как показано на рисунке. Например, чтобы составить таким способом число 15 или 8, потребуется 7 спичек. Какое наибольшее положительное число можно составить из 7 спичек?

1) 31 2) 51 3) 74 4 )711 5) 800

Решение. Начнём проверку из самого большого из указанных чисел 800. Для его составления потребуется 19 спичек. Для следующего числа 711 потребуется 7 спичек, что и требовалось найти.

Ответ: 4).

Задача с дисками . У Егора есть 5 дисков разных размеров. Он хочет построить башню из 4 таких дисков, где каждый следующий диск меньше, чем предыдущий. Сколько различных вариантов таких башен Егор может построить?

1) 4 2) 5 3) 9 4) 12 5) 20

Решение. Для удобства назовём диски M, N, P, F, T (M — самый большой, T- самый маленький). Тогда можно построить башни из 4 дисков: MNPF, MNPT, MPFT, MPTF, NPFT. Всего 5 вариантов.

3. Настольные игры . Шашки, шахматы, нарды, домино, морской бой. Любые другие игры для семейного времяпровождения.

4. Конструирование. Развитие мелкой моторики, воображения.

Например, задача на собирание пазлов .

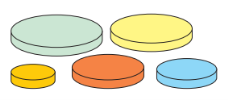
Какие два кусочка пазлов нужно сложить вместе из четырёх, чтобы получился шестиугольник?

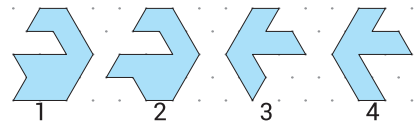
1) 1 и 2 2) 1 и 3 3) 2 и 3 4) 2 и 4 5) 1 и 4

Ответ: 2)

5. Загадки и головоломки . Тренировка нешаблонного решения.

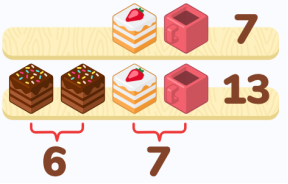
1) 10 2) 11 3) 8 4) 9

Решение. Набор на 1 полке отличается от набора на 2 полке двумя шоколадными пирожными. Значит, на 3 полке 10 пирожных (6:2+7=10).

Ответ: 1)

6. Шахматные задачи . Знакомство с шахматными фигурами, основными правилами игры и координатной плоскостью. Интеллектуальные шахматы — это постоянная «пища» для ума, которую нужно поддерживать. Решать задачи по шахматам может далеко не каждый. Но имея желание тренироваться и интерес к этой игре, можно достигнуть высоких результатов.

7. Логические задачи . Решение логических задач — самый действенный способ развития логики и мышления.Логика — это искусство рассуждать, умение делать правильные выводы. Существует несколько различных методов решения логических задач. Рассмотрим некоторые из них, которые подходят для возрастной группы 5–6 классов.

Метод рассуждений — самый распространенный способ. Этим способом решаются самые простые логические задачи. Его идея состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи.

Задача 1. Три друга.

Три друга — Олег, Коля и Саша — сели на скамейку в один ряд. Сколькими способами они могли это сделать?

Решение.

1) Пускай первым на лавочке сидит Олег, тогда мальчики могут сидеть двумя способами: а) первый Олег, второй Саша и третий Коля, б) первый Олег, второй Коля и третий Саша.

2) Если первым на лавочке сидит Саша, тогда мальчики тоже могут сидеть двумя способами: а) первый Саша, второй Олег и третий Коля, б) первый Саша, второй Коля и третий Олег.

3) Если первым на лавочке сидит Коля, тогда мальчики тоже могут сидеть двумя способами: а) первый Коля, второй Олег и третий Саша, б) первый Саша, второй Коля и третий Олег.

Ответ: 6 способов.

Задача 2. Переливание молока.

Перед вами кувшин, содержащий 4 литра молока. Вам необходимо разделить эти 4 литра поровну между двумя друзьями, но из посуды у вас имеются только еще два пустых кувшина: один, вмещающий 3 литра, и другой, вмещающий 1 литр. Как же поделить молоко поровну с помощью только этих трех сосудов? Придется, конечно, несколько раз переливать молоко из сосуда в сосуд. Но как?

Решение . С помощью кувшина, вмещающего 1 литр, два раза отмерить (получится 2 литра) и перелить в кувшин, вмещающий 3 литра. В первом кувшине останется 2 литра. В итоге у каждого по 2 литра.

Задача 3. Число 66 .

Число 66 надо увеличить в полтора раза, не производя над ним никаких арифметических действий. Как это сделать?

Ответ. Нужно написанное число 66 перевернуть “вверх ногами”.

Задача 4 . Сумма чисел.

Андрей хочет записать целые положительные числа в каждую из 5 клеток так, чтобы произведение двух соседних чисел были такими, как указано на рисунке. Чему будет равна сумма пяти чисел, которые он запишет в клетки?

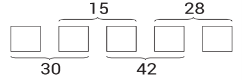
Решение . Начнём с произведения 15. Оно получается, если его множители: 3 и 5. Так как 42 делится на 3, но не делится на 5 нацело, то в первой клетке запишем число 6 (30:5=6), во второй — 5. Дальше в третьей — 3 (15:5=3), в четвёртой — 14 (42:3=14), а в последней — 2 (28:14=2). Итак, 6+5+3+14+2=30.

Ответ: 30.

Задача 5 . Про ужа.

Площадка выложена квадратными плитками трёх разных размеров. Самый маленький квадрат имеет периметр 80 мм. Уж решил отдохнуть, расположившись на лужайке так, как показано на рисунке. Какова длина ужа?

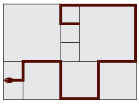
Решение. Периметр самого маленького квадрата 80 мм. Значит, 80:4=20 (мм) длина стороны маленького квадрата. Тогда длина стороны среднего квадрата 20+20=40 (мм), а большого — 20+20+20=60 (мм). Тогда длина ужа 20∙5+40∙5+60∙2=420 (мм).

Ответ: 420 мм.

Задача 6. Кадеты Андрей, Егор и Захар изучают дополнительно различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: «Андрей изучает китайский, Егор не изучает китайский, а Захар не изучает арабский». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?

Решение . Имеется три утверждения. Если верно первое утверждение, то верно и второе, так как ребята изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Андрей не изучает китайский, китайский изучает Егор. Егор изучает китайский язык, Захар — японский, Андрей — арабский.

Метод таблиц . Таблицы хорошо применять, когда устанавливается связь между двумя множествами (можно и между тремя множествами), когда количество элементов во множествах одинаково и неодинаково. Связь можно выразить цифрой 1(или +), а её отсутствие — 0 (или -).

Задача. Андрей, Марсель, Яков и Юра заняли первые четыре места в соревновании по фехтованию, причём никакие два мальчика не делили между собой какие-нибудь места. На вопрос, кто какое место занял, Коля ответил: «Ни первое, ни четвёртое»; Борис сказал: «Второе», а Вова заметил, что он был не последним. Какое место занял каждый из мальчиков?

	Андрей	Марсель	Яков	Юра
Первый	-	-	+	-
Второй	-	+	-	-
Третий	+	-	-	-
Последний	-	-	-	+

Метод графов . Очень часто необходимая информация«замаскирована», представлена неявно, и надо уметь её извлечь. Возникает проблема: как установить логические связи между разрозненными фактами и как оформить в виде единой целой. Видеть ход доказательства и решения задач позволяет метод граф — схем, который делает доказательство более наглядным и позволяет кратко и точно изложить доказательства теорем и решения задач.

Задача. Красный, синий, желтый и зеленый карандаши лежат в четырех коробках по одному. Цвет карандаша отличается от цвета коробки. Известно, что зеленый карандаш лежит в синей коробке, а красный не лежит в желтой. В какой коробке лежит каждый карандаш?

Решение. Обозначим точками карандаши и коробки. Сплошная линия будет обозначать, что карандаш лежит в соответствующей коробке, а пунктирная, что не лежит.

Далее достраиваем граф по следующему правилу: поскольку в коробке может лежать ровно один карандаш, то из каждой точки должны выходить одна сплошная линия и три пунктирные. Получается граф, дающий решение задачи.

Когда обучающийся поглощен желанием разгадать увлекательную проблему, творческий замысел, изобретательность и острота ума достигают пика и проходят превосходную школу. Обнаружение решения или просто знакомство с изящным способом его представления приносит интеллектуальное удовлетворение и эстетическое удовольствие. Решение оригинальных, нестандартных, логических задач — головоломок, задач на соображение и догадку будит мысль, активизирует мыслительную деятельность, развивает творческие способности, стимулирует мышление, усиливает когнитивную активность и способствует развитию творческих навыков. Способность решать логические задачи отражает уровень интеллектуального развития и глубину понимания материала.

Литература:

1. Воронцова Л. Я. Развитие логического мышления на уроках математики // Образование в современной школе.-2007. — 205 с. Текст: непосредственный
2. Дорофеев,Г.В., Шарыгин И. Ф. Математика. Учебник для 5 класса. М.: Просвещение, 2017. — Текст: непосредственный
3. Кондрашенкова Т. А. Формирование общелогических умений при обучении математике в 4–5 классах. / Т. А. Кондрашенкова, И. Л. Никольская // Самостоятельная деятельность учащихся при обучении математике. М.: Просвещение, 1985. — Текст: непосредственный
4. Пойа Д. Математическое открытие. — М.: Наука, 1970. –Текст: непосредственный
5. Фридман Л. М. Психолого-педагогические основы обучения математике в школе. — М.: Просвещение, 1983. — Текст: непосредственный