Метод парных интегральных уравнений



Рассмотрим плоскую динамическую задачу теории упругости в области, представляющей собой плоскость с разрезом -а≤x≤a, y=0 (рис. 1)

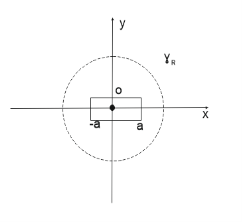
Рис. 1

Этот разрез является математической идеализацией трещины, которая, как предполагается, имеет бесконечные размеры в направлении, перпендикулярном плоскости хоу. Тело будем предполагать однородным и изотропным, Вектор смещения удовлетворяет системе уравнений Ляме

(1)

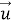
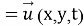
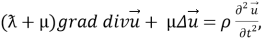
а также соответствующим начальным и граничном условиям. Граничные условия состоят в равенстве нулю напряжений

и на краях трещины и условий на бесконечности. Вместо неизвестных функций u ₁ (x,y,t), u ₂ (x,y,t) удобно ввести потенциалы φ(xy,t) и ψ (x,y,t), полагая

(2)

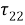
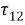
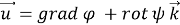
где -орт оси, перпендикулярной к плоскости. XOY.

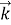
В силу (1) они будут удовлетворять волновым уравнениям

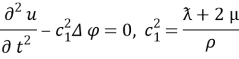
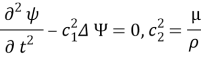
Здесь c ₁ и c ₂ — скорости распространения, воли расширения-сжатия и сдвига.

В дальнейшем мы будем рассматривать только установившиеся колебания тела с частотой , совпадающей с несущей частотой падающей монохроматической волны, которая вызывает эти движения.

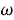
Тогда искомые потенциалы и могут быть предоставлены в виде

, (3)

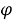
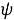
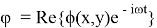
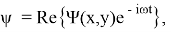
Где (х,у),

(х,у) — комплекснозначные неизвестные функции. Они удовлетворяют уравнениям Гельмгольца

(4)

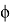
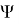
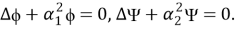
Здесь , представляют собой волновые числа:

. (5)

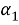
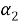
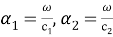
Падающую волну мы будем предполагать плоской распространяющейся под угом к оси ОХ. Если эта волна является волной расширения-сжатия, то ее потенциал могут быть представлены в виде (6):

(6)

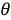
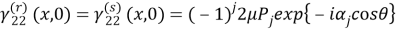
Здесь

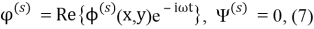
где

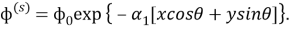
В случая падающей волны сдвига аналогично имеем

, (8)

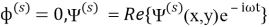
где

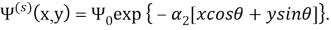
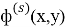
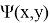
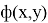
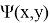
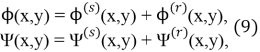
Функции , являются решением уравнениям (4). Представим искомые функции , в виде суммы:

где функции — аналогии функций

для отраженных волн.

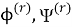
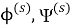
Введём некоторые комплексные функции , которые связаны с напряжениями соотношением:

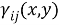
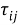
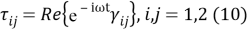
В нашем случае связаны с функциями и формулами:

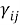
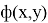
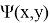
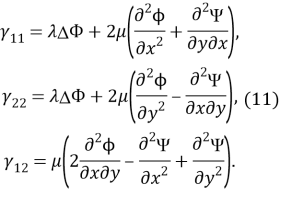
Пользуясь этими формулами, можно найти величины , соответствующие, напряжениям, возникающим при распространении, падающей волны. В случае волны расширения — сжатия:

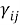
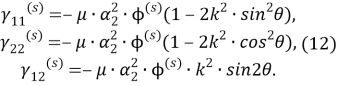
Для волны сдвига:

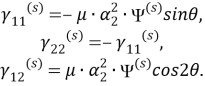
Равенство нулю нормального напряжения на краях трещины запишем в виде:

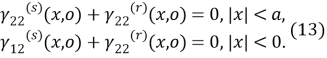
В итоге для неизвестных функций и получим краевую задачу:

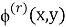
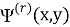
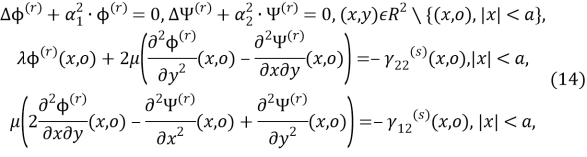
Кроме того должны выполняться условия излучения для при , что обеспечивает единственность решения краевой задали.

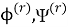
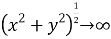
Рассмотрим две вспомогательные задачи.

Задача А:

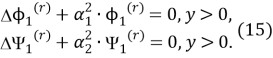
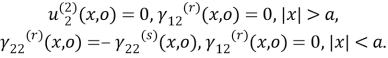
Задача B:

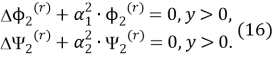
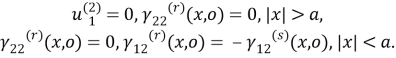
Через обозначим чётное по у продолжение функций на нижнюю полуплоскость, через

— аналогичное нечетное продолжения функций .

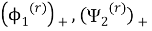
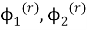
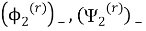
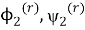
Тогда функции

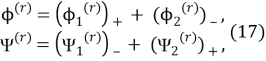
удовлетворяют краевой задаче (14). Таким образом, решение краевой задачи (14) на всей плоскости свелось к решению задач А и В на верхней полуплоскости.

Литература:

1. Викторов И. А. Физические основы применения ультразвуковых волн Рэлея и Лэмба в технике. — М.: Наука, 1966 г.
2. Ляв А. Математическая теория упругости. — М.: Л: ОНТИ, 1935 г.
3. Купрадзе В. Д. Методы потенциала в теории упругости. -М.: Физматгиз, 1963 г.