В статье представлена возможность применения оптимальной теории в области технической диагностики вообще и технической диагностики транспортных средств в частности посредством постановки и решения задачи линейного программирования.
Ключевые слова: линейное планирование, линейное программирование, автотранспортные средства, диагностика, целевая функция, система массового обслуживания.
The article presents the ability to apply optimal theory in the field of technical diagnosis in general, and technical diagnosis of military vehicles in particular through stating and solving a linear programming problem.
Keywords: linear planning, linear programming, vehicles, diagnostics, objective function, queuing system.
- Введение
В повседневной жизни нам часто приходится решать множество задач, чтобы найти оптимальное решение (найти максимальное или минимальное значение целевой функции, определенной на определенном подмножестве евклидова пространства).
Реальность показывает, что большинство задач технического диагностирования транспортных средств сводятся к нахождению минимального значения функции стоимости C(x), связанной с областью эксплуатации и ремонта транспортных средств или ее выходом из строя. Тогда переменной x могут быть параметры, представляющие технические условия (допустимые значения или предельные значения), циклы технического диагностирования и т. п.
Если функция C зависит только от одной переменной x и дифференцируема, то найти ее минимум не составляет труда. Проблема будет сложнее, если C — многомерная функция C(x), где x = (x 1 , …, x n ).
Для решения задач оптимизации при технической диагностике люди часто применяют математические методы, такие как линейное программирование, нелинейное программирование и динамическое программирование, теория массового обслуживания, теория игр, метод сетевых диаграмм и т. д. В действительности мы можем использовать методы линейного программирования для оптимизации количества топлива, потребляемого двигателем транспортных средств, и использовать методы нелинейного планирования для оптимизации. Оптимизировать диапазон параметров средств диагностики, использовать динамическое программирование для выбора технологической последовательности измерения диагностических параметров, использовать теорию краудсорсинга для расчета потока автомобилей транспортных средств, доставленных на диагностику.
Ниже мы построим задачу оптимизации расхода топлива двигателем транспортных средств и продемонстрируем ее решение с помощью симплексного метода линейного программирования.
- Основание
Предположим, что расход топлива Р транспортных средств зависит от 3-х диагностических параметров А, В и С по функциональной зависимости:
P = 0,8S 1 +0,9S 2– 1,1S 3 +2 (1)
Кроме того, если S 1 и S 2 увеличиваются, P увеличивается, а если S 3 увеличивается, P уменьшается.
Очевидно, что P-функция имеет минимум, когда диагностические параметры (при естественных условиях S 1 ≥ 0, S 2 ≥ 0, S 3 ≥ 0) имеют значения: A 0 = B 0 = 0, C 0 = + ∞. Однако в действительности каждый диагностический параметр и каждый конструктивный параметр одновременно влияют на ряд технико-экономических характеристик двигателя и транспортных средств в целом. Например, если увеличить параметры А, В и уменьшить С, это может вызвать изменения. Время запуска двигателя h1, максимальная скорость автомобиля h2, температура запуска двигателя h 3 , частота Минимальное устойчивое вращение коленчатого вала двигателя h4.
Предположим, что соответствующие характеристики имеют следующие отношения зависимости:
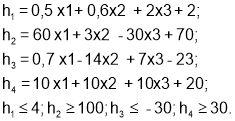
Кроме того, предположим, что по своей физической природе диагностические параметры не могут принимать отрицательные значения, т. е. А ≥ 0; В ≥ 0; С ≥ 0.
Поэтому необходимо определить минимальное значение функции (1) при следующих ограничениях:
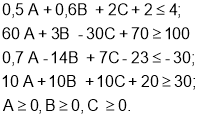
Нахождение минимального значения функции (1) при ограничениях (2) является задачей линейного программирования.
Задача канонического линейного программирования формулируется следующим образом:
Определим минимум линейной функции:
T = T(x 1 , …, x n ) = c 1 x 1 + c 2 x 2 + … +c n x n (3)
задан на подмножестве n-мерного евклидова пространства и определяется ограничениями:
x
i
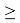
a i1 x 1 + a i2 x 2 + … + a in x n = b i (i = 1…m)(5)
Для решения задач линейного программирования можно использовать множество разных методов, но самым простым и популярным является симплекс-метод.
- Решить задачу линейного программирования симплекс-методом
Процесс решения включает в себя 5 этапов:
3.1. Определить ранг матрицы
A =
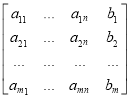
созданный коэффициентами и свободными членами (5). Если ранг матрицы A меньше m, то линейно зависимые строки можно исключить: количество оставшихся строк в матрице должно быть равно рангу матрицы. Считаем ранг матрицы равным m.
3.2. Разобьем переменные x 1 , x 2 ,..., x n на две группы: в первую группу входят m базовых переменных, во вторую группу входят n — m свободных переменных. Для ясности мы рассматриваем x 1 ,...,x m как базовые переменные, а xm+1,...,xn как свободные переменные. Благодаря системе (5) основные переменные представим через свободные переменные:
x
1
=
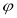
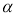
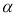
x
2
=
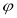
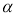
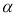
……………………………………..
x
m
=
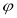
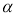
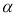
Если все числа 1, 2,..., m неотрицательны, то разделение на базовые переменные и свободные переменные проведено правильно.
Положим xi = i для i = 1…m; x i = 0 для i = m +1… n (7)
У нас есть приемлемый опыт. Если среди чисел 1, 2,..., m есть отрицательные числа, то разделение на базовые переменные и свободные переменные выполнено неправильно и его необходимо переделать.
3.3. Подставив значения базовых переменных в (6) в целевую функцию Т, получим выражение для определения целевой функции через свободные переменные:
T =
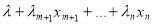

где: λ — значение целевой функции при первом приемлемом решении.
3.4. Предположим, среди чисел есть отрицательные. Если тогда все числа 1k,..., mk положительны, то оптимального решения не существует, а это означает, что если мы возьмем любое приемлемое решение со сколь угодно большим значением xk, мы получим следующие значения: функции T можно будь таким маленьким, как хочешь. Если среди чисел 1k,..., mk отрицательное число, то необходимо продолжить итерационный процесс преобразованием свободной переменной xk в базовую переменную и преобразованием базовой переменной в свободную переменную.
Возвращаясь к изложенной выше задаче оптимизации расхода топлива двигателя автомобиля, поскольку значение постоянной не влияет на нахождение минимума функции, заменим выражение (1) на выражение:
Т’ = 0,8А + 0,9В — 1,1С (8)
Преобразуем неравенство (2) в равенство, введя четыре новые переменные x 1 , x 2 , x 3 и x 4 :
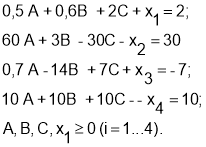
— Ранг матрицы, созданной коэффициентами (9), равен числу уравнений (9), то есть равен 4.
— Принимая A, B, C и x1 в качестве базовых переменных, а x2, x3, x4 в качестве свободных переменных, представим базовые переменные через свободные переменные:
A = 0,474 + 0,012x 2– 0,020x 3 + 0,024x 4 ;
B = 0,524 + 0,004x 2 + 0,0535x 3 + 0,026x 4 ;(10)
C = 0,001–0,009x 2– 0,034x 3 + 0,0051x 4 ;
x 1 = 1,446 + 0,014x 2 +0,046x 3– 0,130x 4 ;
Поскольку первый член в правой части (10) положителен, наше разделение базовых переменных и свободных переменных является правильным. Итак, первое приемлемое решение: A = 0,474; Б = 0,524; С = 0,001; х 1 = 1,146; х 2 = х 3 = х 4 = 0.
— Подставив (10) в (8), получим:
Т’ 1 =0,850 + 0,016х 2 + 0,070х 3– 0,013х 4
Коэффициент при x 4 отрицательный, поэтому нам придется перейти ко второму приемлемому решению.
— Преобразуйте x4 в базовую переменную. В уравнениях (10) отрицательным является только коэффициент при x4. Поэтому преобразуем x1 в свободную переменную и в новом решении x4 = 1,446/0,130 = 11,123.
— Получим второе приемлемое решение: x4 = 11,123;
А=0,474+0,024,11,123=0,741;
В= 0,5244 + 0,026,11,123 = 0,813;
С= 0,001 + 0,051,11,123 = 0,568;
х 1 = х 2 = х 3 = 0.
Сравните второе решение с первым решением:
Т’ 2 = 0,8.0,741 + 0,9.0,813 -1,1.0,568 = 0,700 <0,850 = Т’ 1
Значение целевой функции уменьшено, то есть второе решение близко к оптимальному. Для проверки оптимальности второго приемлемого решения снова представим базовые переменные через свободные переменные:
А = 0,741–0,186х 1 + 0,015х 2– 0,011х 3 ;
Б = 0,813–0,206х 1– 0,01х 2 + 0,062х 3 ;
С = 0,568–0,392х 1– 0,003х 2– 0,016х 3 ; (11)
х 1 = 11,123 –7,832х 1 + 0,106х 2 + 0,361х 3 ;
Подставив базовые переменные (11) в выражение для целевой функции (8), получим:
Т' 2 = 0,700 + 0,098х 1 + 0,051х 2 + 0,06х 3 .
Все коэффициенты в приведенном выше выражении положительны. Поэтому второе решение является оптимальным.
Так, транспортные средства потребляют наименьшее количество топлива Т = Т' +2 = 2,7 при А = 0,741; Б = 0,813; С = 0,568.
Заключение
Излагая и представляя способы решения вышеуказанной проблемы, становится ясно, что линейное программирование играет большую роль и применимо в технической диагностике военной техники в частности и в общей области технической диагностики в целом. Из этой задачи ее можно расширить на многие другие задачи оптимизации технической диагностики, чтобы минимизировать затраты на техническое обслуживание и ремонт транспортных средств в целом.
Литература:
- Фан Куок Кхань, Чан Хюэ Нуонг. Линейное программирование. Издательство «Образование», Ханой, 2000 г.
- Фанкуок Кхан. Исследование операций. Издательство «Образование», Ханой, 2002 г.
- Нгуен Нгок Бан, Фам Нгок Фук, Нгуен Ван Тан. По поводу прикладных математических моделей в КТКС, «Наука и техника», № 68 (III-1994).







