В статье авторы рассматривают процесс выбора двигателя и редуктора для привода движителя гусеничного шасси мобильного робота. Приведены кинематические схемы движения шасси по плоской и наклонной поверхности, описана динамика движения, а также проведён расчёт требуемой мощности двигателя на примере конкретного технического задания. Предложен способ управления приводами шасси, позволяющий ограничить мощность, потребляемую при повороте шасси.
Ключевые слова: гусеничное шасси, мобильный робот, энергетический расчёт.
Роботы представляют собой автоматические устройства, назначение которых состоит в выполнении двигательных и интеллектуальных функций человека [1]. Мобильные роботы выделяются способностью к передвижению и перемещению полезной нагрузки в пространстве. По области применения мобильные робототехнические комплексы (РТК) можно разделить на промышленных роботов, роботов военного и специального назначения. К последней группе относятся, например, роботы-сапёры — наземные мобильные РТК, основная задача которых заключается в работе с потенциально опасными объектами (боеприпасами, взрывными устройствами и т. п.) в дистанционном режиме под управлением оператором. В условиях современной действительности разработка таких роботов становится всё более актуальной задачей. С развитием научно-технического прогресса неизбежно повышается адаптивность и опасность самодельных взрывных устройств, улучшается техническая подготовка организаторов производства таких устройств. Поэтому для эффективного противодействия такого рода угрозам важно поддерживать на должном уровне техническое обеспечение специалистов-сапёров.
Данная научная статья основана на результатах научно-исследовательской работы (НИР), связанной с разработкой системы управления приводами движителей гусеничного шасси робота-сапёра. В ходе выполнения работы было необходимо рассмотреть динамику и кинематику движения шасси по плоской и наклонной поверхности и провести энергетический расчёт привода движителя шасси на примере конкретного технического задания. При этом шасси (мобильная платформа) РТК выполняет функцию обеспечения передвижения всего РТК по заданной траектории с заданными кинематическими параметрами.
Рассмотрим кинематику движения шасси в псевдоиндустриальной среде (плоское движение и прямолинейное движение по наклонной поверхности). Конструкция робота предполагает возможность поворота только бортовым способом. Пусть
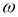
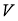
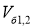
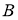
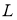
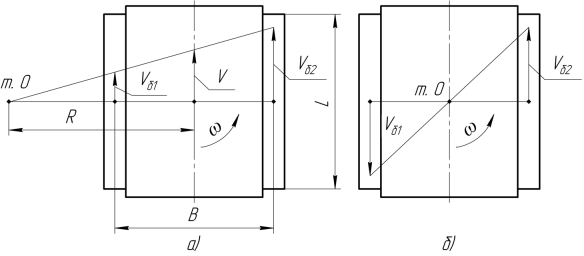
Рис. 1. Схема плоского движения гусеничного шасси
За исключением подъёма по уклону, движение РТК можно представить как плоское. В общем случае плоского движения
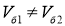
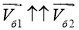
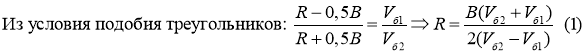
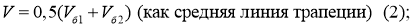
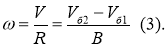
Из этого получим значения скоростей бортов:
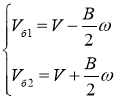
При управлении шасси законы движения задаются именно через скорости бортов
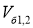
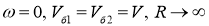
Далее рассмотрим случай б) (рис. 1) — поворот разностью направлений вращения гусениц. В этом случае
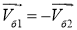
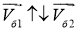
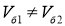
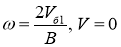
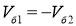
Скорость
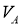
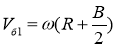
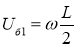
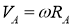
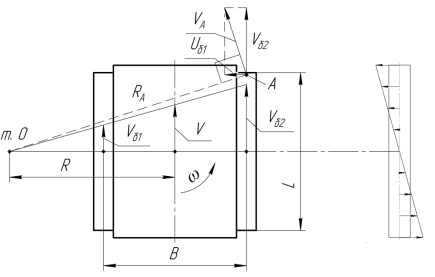
Рис. 2. Скорость точки А корпуса, лежащей на продольной оси гусеницы
Рассмотрим динамику движения шасси [3]. Изобразим схему для случая прямолинейного движения по наклонной поверхности (рис. 3):
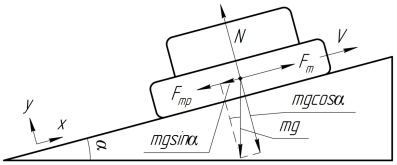
Рис. 3. Схема движения шасси по наклонной поверхности
На данной схеме N — сила реакции опоры, mg — сила тяжести, F т — сила тяги, F тр — сила трения качения гусениц по поверхности, α — угол наклона поверхности. Для обеспечения перемещения по склону движители шасси должны развивать такую F т , которая бы преодолела силы сопротивления движению. Запишем это условие в проекциях на оси x и y:
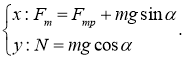
С учётом:
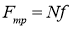
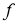
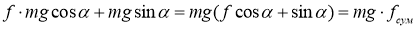
где
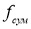
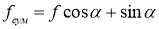
Пусть
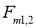
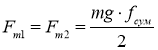
Рассмотрим динамику поворота гусеничного шасси (рис. 4) [3, с. 181].
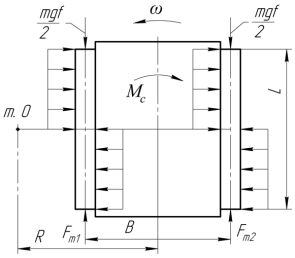
Рис. 4. Схема сил, действующих на гусеничное шасси при повороте
Рассмотрим случай α = 0 (без уклона), тогда
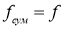
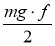
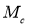
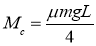
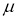
Для определения требуемых сил тяги спроецируем все силы на продольную ось шасси:
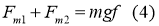
и напишем уравнение моментов сил относительно центра шасси:
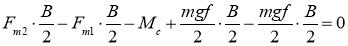
или
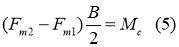
Решая уравнения (4) и (5) совместно, получим:
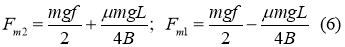
Коэффициент сопротивления повороту
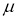
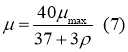
где
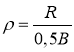
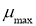
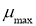
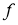
В качестве конкретного примера для проведения энергетического расчёта возьмём следующее техническое задание. Масса и габариты робота должны быть такими, чтобы его можно было погрузить/выгрузить в/из багажник/а легкового автомобиля расчётом из двух человек. Робот должен иметь возможность въезжать по стандартным лестницам жилых домов, разворачиваться на лестничной площадке и проходить в обычный межкомнатный и квартирный дверной проём. При прямолинейном движении робот не должен отставать от человека, идущего шагом со скоростью 4 км/ч.
Исходя из назначения и условий работы робота, зададим требуемые тактико-технические характеристики (ТТХ) на шасси (таблица 1):
Таблица 1
Требуемые ТТХ на шасси
|
Длина (по краям гусениц), не более |
100 см |
|
Ширина (по гусеницам), не более |
60 см |
|
Масса, не более |
80 кг |
|
Максимальный угол подъёма по склону |
|
|
Максимальная развиваемая скорость: |
|
|
-при прямолинейном движении без уклона |
V 1 =1,12 м/с |
|
-при прямолинейном движении по уклону в
|
V 2 =1 м/с |
|
-при повороте на месте |
ω 4 =1,8 рад/с |
|
Ориентировочное время автономной работы |
4 ч |
Необходимо обеспечить возможность движения шасси по разным типам поверхности: асфальт, бетон, грунтовые дороги, снег, трава и т. д.
Основываясь на требуемых ТТХ, зададим требуемые режимы работы шасси робота, которые обеспечат эффективное выполнение его задач:
- Прямолинейное движение без уклона.
В этом случае
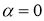
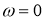
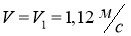
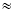
В этом случае
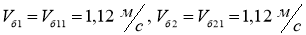
Здесь и далее при расчёте требуемых для указанного точечного режима сил тяги будем ориентироваться на самый тяжёлый для привода режим, т. е. на максимальные теоретически возможные силы сопротивления движению, так как если приводы смогут обеспечить данные силы тяги, то и возникающие меньшие силы тяги они тоже смогут обеспечить. Поэтому примем максимальное значение коэффициента сопротивления:
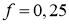
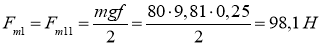
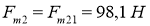
- Прямолинейное движение по наклонной поверхности.
В этом случае
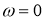
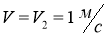
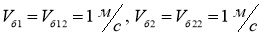
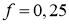
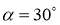
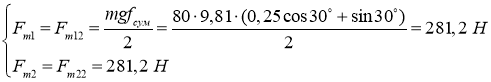
- Поворот без уклона.
Для этого случая
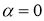
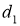
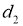
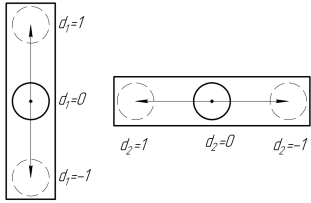
Рис. 5. Схема управления движением шасси с помощью джойстиков
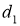
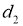
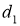
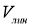
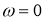
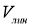
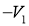
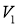
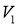
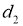
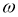
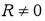
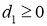
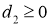
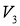
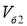
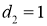
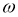
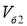
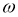
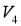
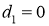
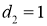
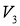
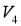
Зададим
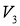
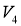
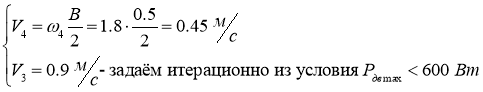
Задаём следующие законы управления бортами:
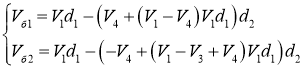
Подставим
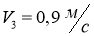
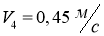
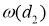
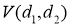
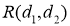
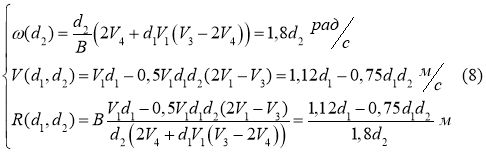
С помощью ПО Matlab получим графики зависимостей
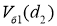
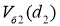
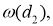
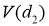
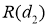
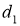
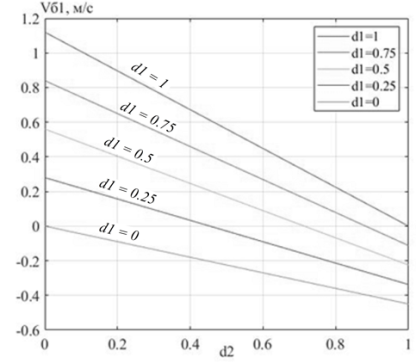
Рис. 6. Семейство графиков
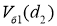
Рис. 7. Семейство графиков
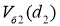
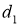
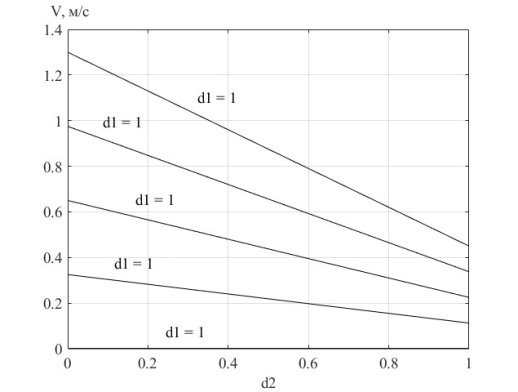
Рис. 8. График зависимости
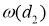
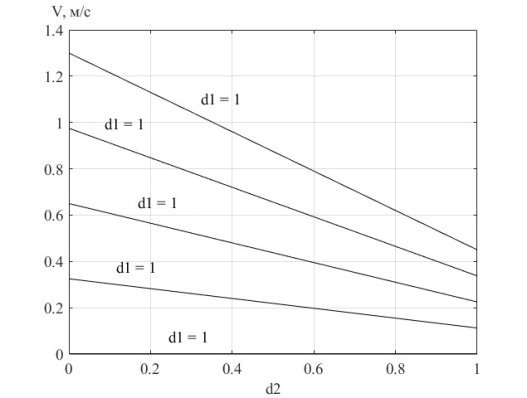
Рис. 9. Семейство графиков
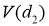
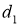
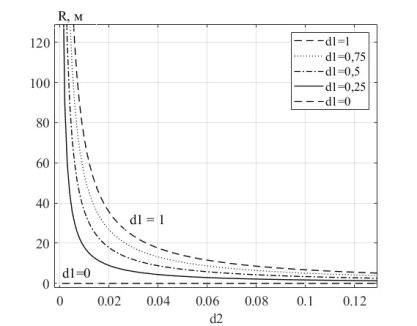
Рис. 10. Семейство графиков
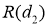
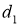
Рассчитаем силу тяги для более тяжело нагруженной забегающей гусеницы. По формулам (6) и (7) и с учётом системы (8) с помощью ПО Matlab построим графики зависимости
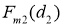
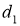
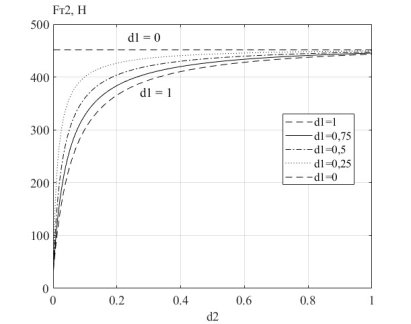
Рис. 11. Семейство графиков
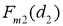
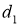
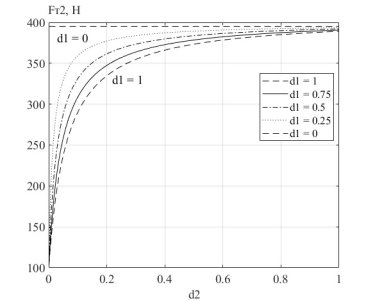
Рис. 12. Семейство графиков
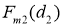
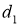
Получим:
— для снега (
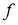
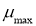
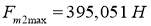
— для сухой грунтовой дороги (
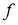
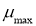
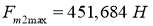
С учётом условия наиболее тяжёлого режима выбираем для расчёта сухую грунтовую дорогу. Рассчитывать силу тяги отстающей гусеницы нет смысла, так как энергетический расчёт будет вестись по забегающей гусенице как более нагруженной.
Для подбора энергоустановки и типа трансмиссии, способных обеспечить требуемые законы движения МРК, проведём энергетический расчёт [4, с. 31].
Пусть i — передаточное отношение редуктора, j — номер точечного режима работы,
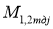
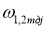
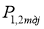
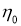
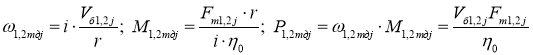
Энергетический расчёт проводим для более нагруженной забегающей гусенице (примем предварительно
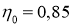
- Прямолинейное движение без уклона.
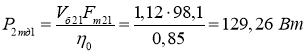
- Прямолинейное движение по наклонной поверхности.
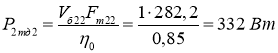
- Поворот без уклона.
Исходя из полученных для третьего режима зависимостей
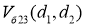
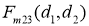
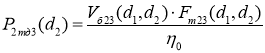
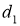
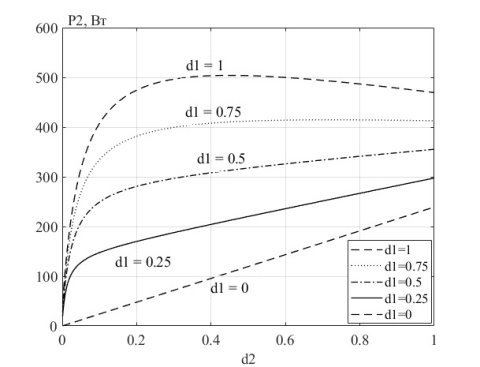
Рис. 13. Семейство графиков
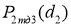
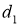
Получим, что максимальное значение
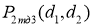
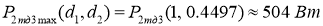
Исходя из максимальной полученной мощности выберем, например, бесколлекторный двигатель постоянного тока (ДПТ) Leadshine ELDM6060V48GL-A5-HD с номинальной мощностью 600 Вт [5].
Выберем передаточное отношение трансмиссии:
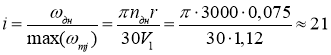
Примем
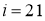
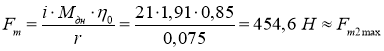
Таким образом, при выбранном передаточном отношении двигатель в номинальном режиме обеспечивает максимальную требуемую силу тяги. Такое значение
В заключение можно сказать, что все поставленные задачи были выполнены: рассмотрены динамика и кинематика движения шасси в псевдоиндустриальной среде, для приведённого технического задания проведён энергетический расчёт, по рассчитанной требуемой мощности выбран двигатель и передаточное отношение редуктора.
Литература:
- Выбор критериев и классификация мобильных робототехнических систем на колесном и гусеничном ходу: учеб. пособие для вузов / Корсунский В. А., Машков К. Ю., Наумов В. Н.; МГТУ им. Н. Э. Баумана. — М.: Изд-во МГТУ им. Н. Э. Баумана, 2014. — 45 с.: ил. — Библиогр.: с. 43. — ISBN 978–5-7038–3881–5.
- Курс теоретической механики: учебник для вузов / Дронг В. И., Дубинин В. В., Ильин М. М. [и др.]; ред. Колесников К. С., Дубинин В. В. — 5-е изд., испр. — М.: Изд-во МГТУ им. Н. Э. Баумана, 2017. — 580 с.: ил. — (Terra Mechanica). — ISBN 978–5-7038–4568–4.
- Основы теории транспортных гусеничных машин: учебник для вузов / Забавников Н. А. — 2-е изд., перераб. и доп. — М.: Машиностроение, 1975. — 447 с.: ил. — Библиогр.: с. 441–442.
- Состав и характеристики мобильных роботов: учеб. Пособие по курсу «Управление роботами и робототехническими комплексами». / К. Ю. Машков, В. И. Рубцов, И. В. Рубцов. — М.: Изд-во МГТУ им. Н. Э. Баумана, 2014. — 75, [1] с.: ил.
- Паспорт двигателя Leadshine ELDM6060V48GL-A5-HD. URL: https://www.leadshine.com/legacys/ELDM6060V48GL-A5-HD(V2.0).html







