Решается задача трисекция угла, которая не решена до сих пор в общей форме.
Ключевые слова: угол, биссектриса, деление угла, хорда, дуга, параллельность прямых, окружность.
В 1837-м году французский математик П. Вансел пришел к выводу, что решение уравнения
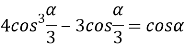
связано с кубическими радикалами и поэтому невозможно делить угол на три равные части с помощью циркуля и линейки. Отсутствие алгебраического решения задачи не означает, что она не имеет геометрического решения.
Мною эта задача была исследована, и я нашел ее замечательное решение. Ниже предлагается одно из этих решений.
Анализ
Пусть угол
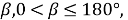
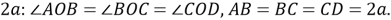
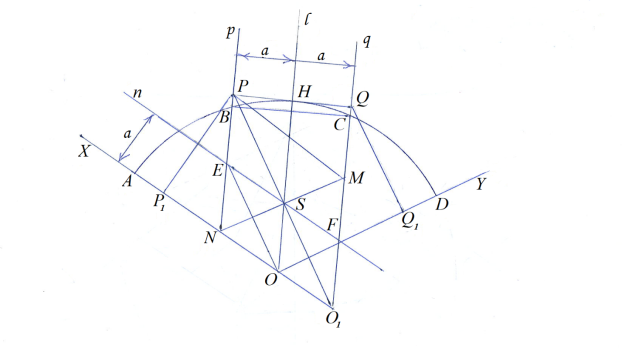
Рис. 1
Шаг 1
. Проведем биссектрису
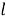
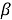
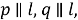
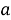
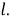
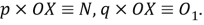
Шаг 2. Обозначим
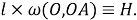
Шаг 3
. Проведем через точку
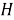
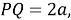
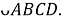
Шаг 4.
Проведем прямые
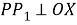
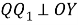
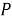
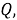
Шаг 5. На расстоянии
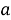
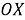
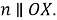
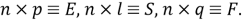
Шаг 6.
Образовываются ромбы
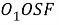
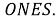
Шаг 7.
Отрезок
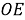
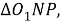
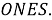
Шаг 8.
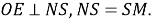
Шаг 9.
Следовательно,
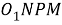
Шаг 10.
Значит,
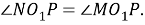
Шаг 11.
Поэтому отрезок
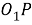
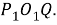
Шаг 12.
По определению биссектрисы угла
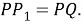
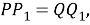
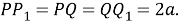
Шаг 13.
Следовательно, угол
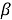
Построение
Пусть задан угол
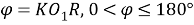
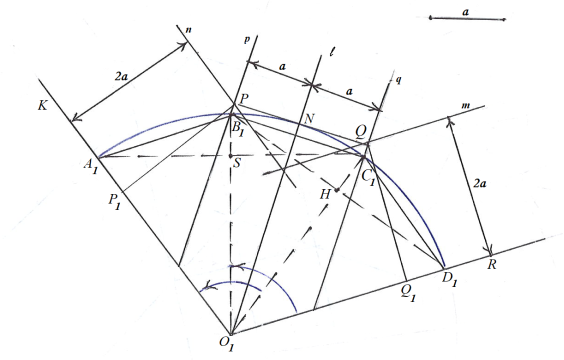
Рис. 2
Шаг 1. Проведем биссектрису
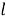
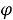
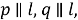
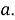
Шаг 2.
Проведем прямые
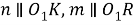
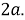
Шаг 3.
Обозначим
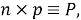
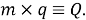
Шаг 4.
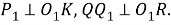
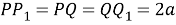
Шаг 5.
Обозначим
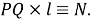
Шаг 6.
Проведем дугу окружности
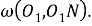
Шаг 7.
Обозначим
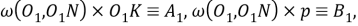
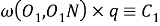
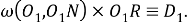
Шаг 8.
По анализу получим
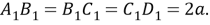
Шаг 9. Хорды равны, значит равны и дуги.
Шаг 10. Следовательно,
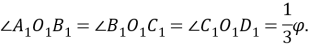
Угол разделен на три равные части.
Доказательство
Шаг 1.
Пусть
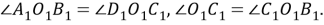
Шаг 2. Поэтому треугольники
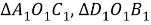
Шаг 3.
Проведем биссектрису
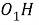
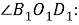
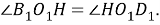
Шаг 4.
Проведем биссектрису
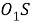
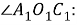
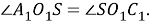
Тогда так как
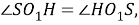
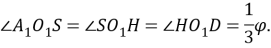
Ч. т. д.
Исследование
Этот способ можно применить для любого угла
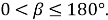
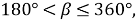
Литература:
- Адлер, А. Теория геометрических построений. Л.: Государственное учебно-педагогическое издательство. 1940. — 232 с.
- Аргунов, Б.И., Балк, М. Б. Элементарная геометрия. М.: Просвещение. 1966. — 368 с.







