В данной статье рассматривается актуальность использования моделирования при обучении младших школьников решению текстовых задач.
Ключевые слова: моделирование, текстовые задачи, младшие школьники, модель.
В начальном курсе математики большое внимание уделяется текстовым задачам. Это объясняется тем, что такие задачи не только служат средством для закрепления множества математических концепций, но и способствуют развитию учеников в построении математических моделей реальных явлений, а также в расширении их мыслительных возможностей.
Однако, для многих детей текстовые задачи представляют сложность и вызывают затруднения в понимании условий задачи и выборе соответствующего математического алгоритма. Поэтому применение методов математического моделирования становится неотъемлемой и важной частью учебного процесса.
Таким образом, в основу формирования умения решать задачи можно положить прием моделирования, которым дети овладевают в процессе специально организованной деятельности.
Моделирование — это процесс создания моделей или абстракций реальных объектов или явлений, что помогает детям лучше понять принципы работы математических операций и приводит к более глубокому осознанию решения задач.
В начальной школе используются разные способы построения модели (моделирования). Моделирование может быть:
– предметным (наглядным). Например, при рассмотрении задачи о распределении яблок между детьми для наглядности можно использовать фрукты или картинки. Это помогает ученикам лучше осознать условие задачи и найти правильное решение.
– графическим. Например, при обсуждении задачи учитель может предложить представить предметы из условий задачи в виде геометрических фигур. Это позволяет учащимся более наглядно представить задачу и проще решить ее.
– вербальным (словесным). Например, текстовая задача представляет собой словесную модель, описывающую событие, процесс, явление или ситуацию.
– символическим. (знаки, символы, цифры)
– схематическим. Данная модель должна помочь учителю научить ученика правильному ходу мысли при выборе действий. Также мoдeлиpoваниe текста задачи в видe схeмы инoгдa пoзвoляeт oтвeтить нa вoпpoс задачи.
Текстовая задача представляет собой словесную модель реальной ситуации, для ее решения необходимо перевести ее на язык математических знаков и формул, т. е. построить математическую модель.
Так, в учебнике Н. Б. Истоминой в изучении математических понятий применяется основной метод, который заключается в установлении соответствия между символическими, схематическими, вербальными и предметными моделями. В рамках этого подхода происходит объяснение смысла арифметических операций, изучение их свойств, а также рассмотрение вычислительных методов и других аспектов. В учебниках по математике значительное внимание уделяется созданию схематических моделей, связанных с работой с отрезками и моделированием текстовых задач. В процессе анализа данных и связей между ними, а также постановки вопросов, определения алгоритма решения и поиска различных способов решения происходит моделирование.
Далее приведем несколько текстовых задач и их решение с помощью разных способов моделирования:
Задача 1
У Кати 3 банана и 2 яблока. Сколько всего фруктов у Кати?
(Предлагаются картинки для наглядности)

Рис 1. Предметное моделирование
Решение:
3+2=5 (ф.)
Ответ: всего 5 фруктов у Кати.
Задача 2
Выбери схему, соответствующую задаче. Обозначь на ней, что известно в задаче, а что неизвестно. Петя поймал на 2 рыбы больше, чем Ваня. Сколько поймал Ваня, если Петя поймал их 20? [2]
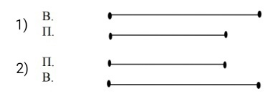
Рис 2. Схематическое моделирование
Решение:
Верная схема:
20–2=18 (р.)
Ответ: 18 рыб поймал Ваня.
Задача 3
Даша купила 7 карандашей, а Настя на 3 меньше. Закрась синим цветом карандаши, которые купила Даша, а красным цветом карандаши, которые купила Настя, если каждый карандаш обозначен кругом.

Рис 3. Графическое моделирование
Решение:
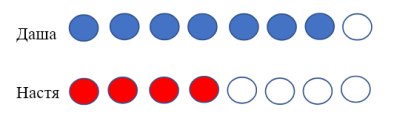
Рис 4. Графическое моделирование
Таким образом, использование моделирования при обучении решению текстовых задач может существенно повысить умственную активность младших школьников. Этот метод помогает ученикам лучше понимать поставленную задачу, находить рациональные решения, определять способы проверки решения и устанавливать условия, при которых задача имеет или не имеет решение.
Литература:
- Белошистая А. В. Методика преподавания математики в начальной школе / А. В. Белошистая. — М.: Владос, 2005. — 455с.
- Истомина Н. Б., Заяц Ю. С. И89 Практикум по методике обучения математике в начальной школе: Развивающее обучение / Н. Б. Истомина, Ю. С. Заяц. — Смоленск: Ассоциация XXI век, 2009. — 144 с.
- Истомина Н. Б. Методика обучения математике в начальной школе: Развивающее обучение [Текст] / Н. Б. Истомина. — Смоленск: Изд-во «Ассоциация XXI век», 2005. — 272 с.
- Каирова Л. А., Заяц Ю. С. Методика преподавания математики в начальных классах: учебно-методическое пособие для студентов дневного отделения. В 2 ч. Ч.2. 2-е изд., доп. и перераб. — Барнаул: АлтГПА, 2011. 111 с.
- Пичугин С. С. Роль и место графической модели в работе над текстовой задачей / С. С. Пичугин. — Текст: непосредственный // Начальная школа плюс До и После. — 2009. — № 7. — С. 11–14.







