Разработаны предложения по оценке состояния помеховой обстановки на основе прогнозирования с использованием линейной модели.
Ключевые слова: помехи, излучения, метод.
В современном мире наблюдается рост источников радиоизлучений и увеличение их концентрации по территории, что соответственно, может привести к проблеме электромагнитной совместимости. Для того, чтобы избежать влияния помех на функционирование радиоэлектронных средств (РЭС) к существующим методам борьбы с ними относятся [1, с.56] применение фильтров, экранирование, разнесение, подавление (в частотной или временной области) и др.
Данные методы являлись актуальными несколько раньше, а сегодня могут не обеспечить требуемый уровень защиты по причине значительного роста количества источников излучений и уровня помех от них.
В складывающейся ситуации в целях недопущения влияния уровня помех на функционирование РЭС, предлагается осуществить его прогнозирование с целью недопущения превышения его допустимого значения.
Известно, что одинаковые и почти неизменные изменения уровня помех можно представить уравнением следующего вида [2, с.23]:

где


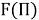
Используя уравнение (1), найдем


Перейдём от рассмотренного выше уравнения (2) к уравнению, которое будет связывать текущее значение параметра






Решим уравнение (2) относительно


Для линейной модели:
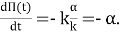
Уравнение (4) это линейное однородное дифференциальное уравнение (ЛОДУ). Его решением относительно


где


Значение постоянной






В результате выражение для уравнения отказа запишется как:

Для линейной модели дрейфа:

В данной модели скорость изменения уровня помех остается неизменной, в то время как его значение является случайной переменной, распределенной по произвольному закону.
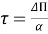
где

В рассматриваемом случае взаимно-однозначной зависимостью связаны случайные величины



Так как плотность распределения

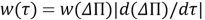
Из равенства (9) следует:

Тогда:

Для случая, когда случайная величина


Формула (14) легко преобразуется к следующему виду:

где

Примеры численных расчетов плотности распределения времени до выхода уровня помех за пределы допустимых значений для выбранной линейной модели представлены на графиках 1 и 2.
Анализ графиков показывает, что с увеличением математического ожидания (МО) случайной величины П (разности между начальным и предельным значениями уровня помех) полученная плотность распределения времени сдвигается по оси времени в сторону больших значений, а при уменьшении МО — в сторону меньших, т. е. чем выше начальное значение случайного параметра, тем больше времени потребуется для того, чтобы этот параметр вышел за допустимые пределы [3, с.97]. Изменение же значений среднеквадратического отклонения П приводит соответственно к увеличению (уменьшению) разброса значений случайного времени выхода уровня помех за пределы допустимых значений относительно его МО.
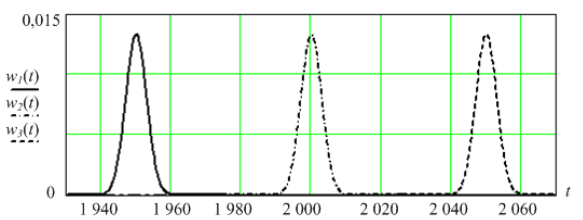
Рис. 1. ПРВ до выхода уровня помех за пределы допустимых значений относительно его МО для линейного закона изменения параметра при случайном коэффициенте П для w 1 ( t ) М П = 1950; для w 2 ( t )
М П = 2000; для w 3 ( t ) М П = 2050; П = 3, а = 1
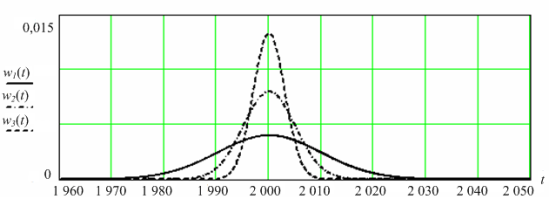
Рис. 2. ПРВ до выхода уровня помех за пределы допустимых значений относительно его МО для линейного закона изменения параметра при случайном коэффициенте П для w 1 ( t ) П = 10; для w 2 ( t ) П = 5; для w 3 ( t ) П = 3; М П = 2000, а = 1
Таким образом, полученные значения плотности распределения временит достижения уровнем помех предельного значения могут быть использованы для прогнозирования времени измерения уровня помех, при котором состояние помеховой обстановки окажется в пределах допустимых значений.
Литература:
- Киселев А.В, Артюшенко В. В. Радиопомехи и помехоустойчивый приём. Методы повышения помехазащищённости. — М.: НГТУ, 2022. — 72 с.
- Киселев А.В, Савиных И. С. Радиопомехи и помехоустойчивый приём. – М.: Новосибирск, 2019. — 88 с.
- Перфилов О. Ю. Радиопомехи. — М.: Горячая линия, 2017. — 110 с.
- Климашов Б. М. Защита автономных радиолокационных систем от внешних помех. – М.: СамГТУ, 2005. — 416 с.
- Защита радиолокационных систем от помех. Состояния и тендеция развития. — М.: Радиотехника, 2003. — 271 с.







