Анализ и синтез сложных систем практически любой природы связаны с решением проблемы многокритериальности. К большому сожалению, в преобладающем большинстве отраслей, не является исключением и строительное материаловедение, за редким исключением [1] оптимизация по векторному критерию практически не используется. Обычно большинство авторов ограничиваются однокритериальной оптимизацией без надлежащего ранжирования критериев и минимизации размерности критериального пространства [2]. Практически не используются и известные формализованные методы решения задач с ограничениями (в частности, метод последовательных уступок).
Заключение об эффективности функционирования сложных систем невозможно сделать на основании регистрации какого-либо одного показателя. Оценка, как правило, является многокритериальной и не сводится к стандартной оценке качества по одному критерию. Задания всей совокупности критериев часто недостаточно для выделения важнейшего: необходима дополнительная информация об относительной важности каждого из них. Ниже ограничимся только детерминированными задачами управления, в которых множеством критериев полностью определяется качество управления.
В рассматриваемых задачах критериями 
являются числовые функции, заданные на множестве стратегий управления. Без нарушения общности рассуждений будем полагать, что по каждому из критериев качество системы тем выше, чем больше значение критерия (если не оговорено противное). Считается, что стратегия 
предпочтительнее стратегии 
, если справедливы неравенства
,
.
Предполагается, что хотя бы одно из неравенств — строгое. Если 
, то стратегии и считаются одинаковыми по качеству.
Наиболее серьезной при оценке качества процессов и систем является проблема неопределенности в постановке исходной задачи. С этим непосредственно связана проблема нормализации множества критериев качества, задания приоритетов (степени важности) для элементов множества критериев.
В некоторых случаях возможна оценка процесса или системы по некоторому обобщенному глобальному критерию качества 
, являющемуся некоторой функцией локальных критериев 
. При такой оценке обычно используются два метода.
В первом оценка сводится к решению задачи с ограничениями, имеющей две модификации. В первой из всего множества критериев выделяется основной критерий 
, по которому и проводится оценка качества; остальные критерии 
ограничиваются условиями: «не меньше, чем» или «не больше, чем». Во второй множество критериев представляется в виде упорядоченного по степени важности множества, а затем проводится последовательная оценка качества. Критерий оптимальности из всего множества критериев выбирается субъективно.
Второй метод состоит в формировании глобального критерия качества в виде суммы локальных, взятых со своими весовыми коэффициентами (скаляризация, свертывание критериев). Эффективность метода зависит от степени объективности этих констант.
Нормализация (приведение критериев к единой мере) связана с различными размерностями локальных критериев. Она может проводиться с учетом оптимального значения 
для каждого локального критерия и определения отклонений 
. Успешное решение проблемы нормализации зависит от того, насколько точно определены оптимальные значения локальных критериев.
При анализе и синтезе сложных систем различной природы (композиционные материалы модульной структуры, тренажные и обучающие комплексы для подготовки операторов транспортных систем, механические колебательные системы и т. д.) нами эффективно использовалась приводимая ниже методика выбора весовых констант. А именно, процедура определения весовых констант 
в глобальном аддитивном критерии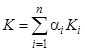 
включала:
- задание начальных значений весов 
;
- вычисление интегральной оценки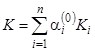 
;
- определение коэффициентов корреляции
,
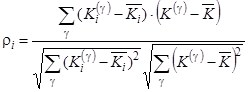частных критериев качества с глобальным критерием K;
- уточнение значений весовых констант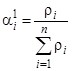 
, ;
- уточнение значений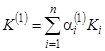 
.
Итерационная процедура осуществляется до выполнения условия 
В результате будет получена оценка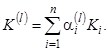 
Найденные таким образом значения весовых констант не зависят от их начальных значений , а определяются только долей участия частных критериев в глобальном критерии качества K. Методика легко обобщается и на случай, когда
.
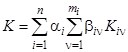Например, при оценке качества композита [3] частными критериями являются свойства:прочность, твердость, реологические свойства и т. д. В качестве критериев 
рассматриваются параметры кинетических процессов набора прочности, твердости и т. д. (определяются точкой в факторном пространстве: точки экстремума, экстремальные значения, точки перегиба и т. д.). Константы 
определятся аналогично определению .
Приведенная процедура использовалась и для объективизации субъективной оценки оператором эргатической транспортной системы технических характеристик объекта с точки зрения управления, а также имитационных характеристик тренажных комплексов (оценка имитационных характеристик непосредственно связана с задачей объективного контроля качества моделирования объекта и сводится ксравнению управляющих воздействий в системах «оператор-объект» и «оператор-модель объекта»). Здесь в комплекс показателей, характеризующих деятельность оператора, входили:
- — точность выдерживания заданных параметров движения, сохранения безопасных режимов движения при отказах оборудования;
- качество выполнения дополнительных задач, непосредственно не связанных с движением: надежность восприятия, время выполнения двигательных действий и т. д.;
- структура сбора информации (частота и длительность фиксации, маршруты перемещения и время переноса взгляда, дискретность восприятия);
- параметры психических процессов обнаружения, опознания и принятия решения;
- параметры, определяющие психофизиологическую напряженность оператора;
- субъективные мнения операторов (данные опроса, бесед).
На сегодня ни одну из затронутых выше проблем (с точки зрения практического использования методик) пока нельзя считать решенной до конца (на уровне когнитивного моделирования). Так, предварительная оценка деятельности оператора транспортной системы производилась на основе определения отклонений от заданных параметров движения в некоторый фиксированный момент времени или максимальных отклонений на некотором интервале (например, отклонение от заданной траектории при ручной посадке, взлете, маневре и т. д.). По полученным данным строились функции или плотности распределений, определялись моменты распределения (математическое ожидание, дисперсия, эксцесс, асимметрия и т. д.). При оценке качества управления в аварийной ситуации определялись максимальные отклонения от заданных величин; строились функции распределения отклонений для оценки вероятности выхода параметров за пределы безопасных значений. Осуществлялся корреляционно-спектральный анализ параметров движения. Это дало возможность определить не только средние и среднеквадратические отклонения в выдерживании заданного параметра 
, но и степень колебательности процесса. Для обеспечения необходимой точности полученных характеристик использовались реализации процессов большой длительности, что потребовало больших объемов вычислительных работ. При оперативных оценках управления пользовались математическим ожиданием 
, среднеквадратическим отклонением 
и степенью колебательности процесса
.
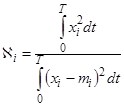Если 
— амплитуды гармоник 
в разложении 
в ряд Фурье на отрезке 
, то оценка колебательности процесса принималась в виде
.
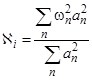Интегральная оценка производилась по значению
.
При заданной дисперсии 
решением изопериметрической задачи вариационного исчисления можно показать, что 
, поэтому интегральная оценка 
принималась в виде
,
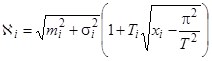— время переходного процесса в контуре стабилизации заданного параметра 
(при управлении в 
-ом установившемся режиме оператором обычно выдерживаются не более трех параметров (
; в горизонтальном полете — скорость, курс, высота; при выполнении спирали — скорость, крен, вертикальная скорость)). При одновременной оценке управления по всем параметрам каждого из установившихся режимов использовали безразмерный аддитивный глобальный критерий:
.
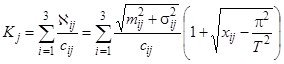Заметим, фактически выбор значений 
на выдерживание каждого 
-го параметра равносилен введению значений весовых констант с присущими этому элементами субъективизма (избавиться в известной степени можно воспользовавшись приведенной выше методикой их выбора).
Эффективность предложенных подходов к решению проблемы многокритериальности подтвердилась при проектировании композитов и оценке имитационных характеристик тренажеров транспортных систем.
Литература:
1. Гарькина И. А., Данилов А. М. Управление в сложных технических системах: методологические принципы управления / Региональная архитектура и строительство, № 1 (12), 2012. — С.39–43.
2. Данилов А. М., Логанина В. И., Смирнов В. А. Анализ показателей лакокрасочных покрытий методом главных компонент / «Известия КазГАСУ», № 1 (11), 2009. — С.243–246.
3. Гарькина И. А., Данилов А.М Управление качеством материалов со специальными свойствами / Проблемы управления. — 2008. — № 6. — С. 67–74.
