Рассмотрены особенности моделирования систем с использованием блока чистого запаздывания. Выявлены случаи некорректной работы блока, при времени запаздывания равном нулю. Приведены способы устранения некорректной работы блока. Приведены варианты программной корректировки структурной схемы модели.
При моделировании систем управления в пакете Simulink, как правило, используется блок чистого запаздывания, так как большинство реальных объектов обладает этим запаздыванием. Пример такой модели приведен на рисунке 1.
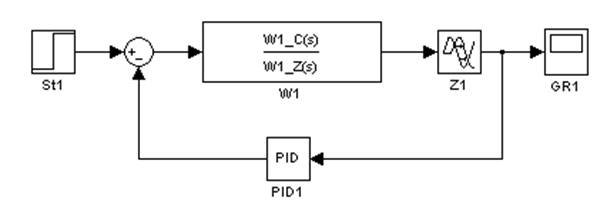
Рис. 1. Модель замкнутой системы управления (Z1)
Чтобы каждый раз не менять параметры модели, их задают в виде переменных, например параметры для блока чистого запаздывания приведены на рисунке 2.
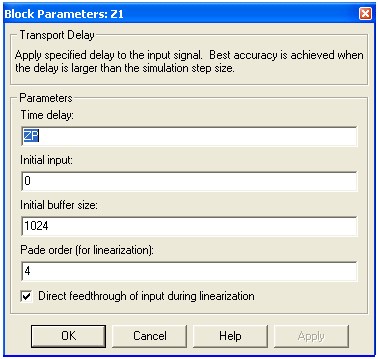
Рис. 2. Настройки блока чистого запаздывания
Timedelay — время запаздывания в секундах.
Initialinput — начальное значение входного сигнала.
Initialbuffersize — размер буфера для хранения сигнала задержки.
Padeorder — Порядок рада Паде для аппроксимации выходного сигналя.
В данном случае, время чистого запаздывания задается идентификатором ZP. Обозначив, таким образом, переменные модели идентификаторами удобно управлять моделями из M-файлов.
Возьмем объект с передаточной функцией:
![]()
Оптимальные настройки ПИ — регулятора для данного объекта составляют Кр=2,6; Ти=7,5.
Напишем следующий М-файл:
%открываем модель
openZ1
% параметры передаточной функции
W1_C= [1]; W1_Z= [50 20 1];
% параметры регулятора
Kr1=2.6; Ti1=7.5; Td1=0;
% значение запаздывания
ZP=5;
% запускаем модель
simZ1
% строимграфик
G1=GR1(:,2); figure; plot(tout,G1, 'b'),grid;
Выполнив файл, получим график переходного процесса, приведенный на рисунке 3.
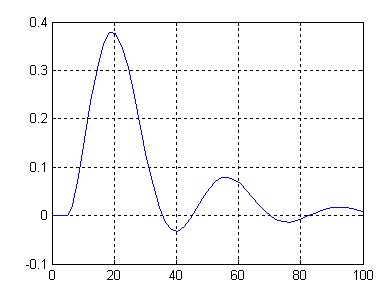
Рис. 3. Переходный процесс для передаточной функции W1(s)
Возьмем объект с этой же передаточной функцией, но не обладающим чистым запаздыванием.
![]()
Оптимальные настройки ПИ — регулятора составляют Кр=20; Ти=0.3. Изменим соответствующие строки M-файла:
% параметры регулятора
Kr1=20; Ti1=0.3; Td1=0;
% значение запаздывания
ZP=0
В результате получим переходный процесс, приведенный на рисунке 4.
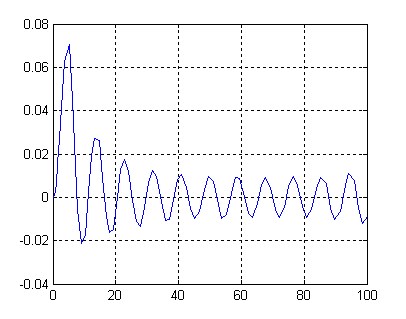
Рис. 4. Переходный процесс для передаточной функции W2(s)
Как видно из рисунка 4 в системе появились незатухающие колебания, чего в принципе быть не должно, т. к. настройки регулятора являются оптимальными.
Проверим это утверждение. Сформируем переходный процесс аналитическим способом. Для этого напишем M-файл со следующими командами:
% Передаточная функция объекта
Wo=tf([1], [50 20 1])
% Передаточная функция регулятора
Wp=tf([6 1], [0.3 0])
% Передаточная функция замкнутой системы
Wc=Wo/(1+Wo*Wp)
% Строим график
step(Wc,100),grid
В результате получим переходный процесс, приведенный на рисунке 5.
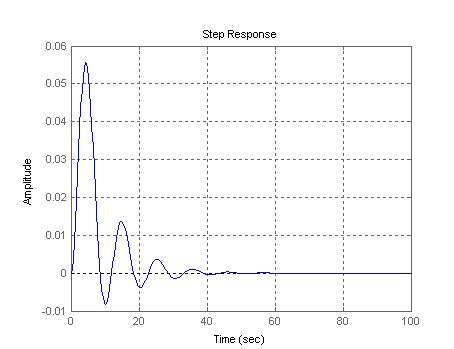
Рис. 5. Переходный процесс
Как видно их рисунка 5 переходный процесс является затухающим. Дело в том, что колебания в процесс вносит блок чистого запаздывания при нулевом значении времени запаздывания. К сожалению, это недоработка разработчиков пакета MATLAB. Не помогает также установка в ноль параметра Padeorder (количество членов ряда Пада).
Можно рассмотреть два варианта, чтобы обойти эту проблему.
Первый вариант — это программно добавлять и удалять блок чистого запаздывания в зависимости от значения времени запаздывания. Фрагмент, реализующий этот вариант, приведен в следующем М-файле:
ZP=5;
f=find_system('Z2', 'BlockType', 'TransportDelay')
u=char(f);L=length(u);
if (ZP==0) & (L==5)
%удаляем блок чистого запаздывания
delete_block('Z2/Z1');
delete_line('Z2', [300 40]);
delete_line('Z2', [355 40]);
add_line('Z2', [280 40;400 40]);
add_line('Z2', [380 40;380 130; 230 130]);
end
if (ZP>0) & (L==0)
%устанавливаем блок чистого запаздывания
delete_line('Z2', [365 40])
add_block('simulink/Continuous/Transport Delay','Z2/Z1','delay','ZP')
set_param('Z2/Z1','Position', [320 25 350 55])
add_line('Z2', [285 40;320 40])
add_line('Z2', [350 40;410 40])
add_line('Z2', [380 40;380 130; 230 130])
end
Если ZP>0 то модель будет выглядеть как на рисунке 1. Если ZP=0 блок чистого запаздывания автоматически удалится, и модель будет выглядеть, как показано на рисунке 6.
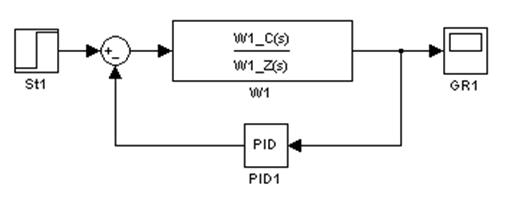
Рис. 6. Модель с удаленным блоком (Z2)
Хотя фрагмент M-файла и является рабочим, и тестировался автором на реальной модели — это не самый лучший вариант. Его можно повторить только на конкретной модели, где координаты, по которым размещены блоки и соединительные линии имеют конкретные значения. В противном случае придется менять все координаты под свою модель.
Второй вариант заключается в байпасировании блока чистого запаздывания. Поместим в модель еще два усилителя B1 и B2, как показано на рисунке 7.
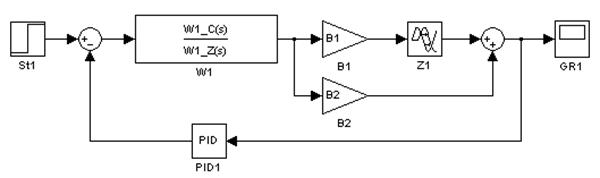
Рис. 7. Модель замкнутой системы управления (Z3)
В приведенной модели от значений коэффициентов B1 и B2, будет зависеть, по какому «пути» пойдет сигнал. Если B1=1 и B2=0 сигнал пойдет через блок запаздывания. Если B1=0 и B2=1 сигнал пойдет в обход блока запаздывания. Остается только проанализировать значение времени запаздывания ZP и в зависимости от него установить коэффициенты B1 и B2.
Для этого напишем следующий фрагмент M-файла.
% значение запаздывания
ZP=0;
if ZP==0
B1=0; B2=1;
else
B1=1; B2=0;
end
% запускаем модель
sim Z3
Если выполнить данный M-файл, получим переходный процесс, приведенный на рисунке 8.
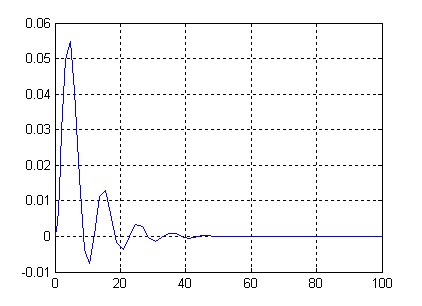
Рис. 8. Переходный процесс в модифицированной модели
Как видно из рисунка 8 незатухающие колебания в системе исчезли. Не смотря на то, что в данном варианте используется два дополнительных блока, код управления такой моделью короче, а самое главное, код не зависит от геометрического расположения блоков модели.
Литература:
1. Ротач В. Я. Теория автоматического управления теплоэнергетическими процессами. М.: Энергоатомиздат, 1985. 296 с.
2. Ануфриев И. Е. MATLAB 7 / И. Е. Ануфриев, А. Б. Смирнова, Е. Н. Смирнова.– СПб.: БХВ-Петербург, 2005.– 1104 с.
3. Черных И. В. Моделирование электротехнических устройств в MATLAB, SimPowerSystem и Simulink. Питер ДМК, 2008..– 286 с.







