Разработана компьютерная модель процесса ротационной сборки цилиндрических деталей с малыми зазорами в программном комплексе SolidWorks. Изготовлена экспериментальная установка для ротационной сборки. Приведены результаты компьютерного моделирования и серий экспериментов на сборочной установке ротационного типа и сделан вывод об адекватности разработанной компьютерной модели.
Ключевые слова: ротационная сборка, цилиндрическая деталь, компьютерная модель.
Для повышения надежности сборки цилиндрических соединений, в частности сборки радиальных роликовых подшипников, предложен ротационный метод сборки [3]. Разработанное на его основе устройство [2] может найти широкое применение в автоматизированной сборке подшипников различного типа, а также цилиндрических соединений с малыми зазорами.
Поскольку сопрягаемые цилиндрические поверхности разнообразны по номинальным размерам, величинам зазоров и точности сопряжения, целесообразна разработка компьютерной модели ротационной сборки.
Для создания компьютерной модели использован программный комплекс SolidWorks Premium 2011, предназначенный для автоматизации работ промышленного предприятия на этапах конструкторской и технологической подготовки производства изделий любой степени сложности и назначения.
Для исследования ротационной сборки в SolidWorks был спроектирован процесс сборки узла, состоящего из двух деталей (рис. 1).
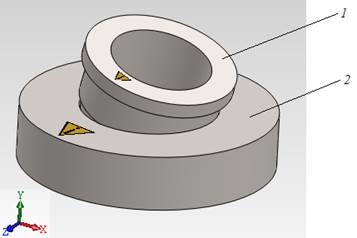
Рис. 1. Сборка цилиндрического соединения в пакете SolidWorks
Здесь внутреннее кольцо 1 свободно в пространстве и лежит на детали 2 под некоторым углом перекоса осей сопрягаемых деталей. Деталь 2 имеет только одну степень подвижности — вращение вокруг своей оси. Угол между осями деталей варьировался в пределах 7°…25°.
Сечения деталей 1 и 2 показано на рис. 2.
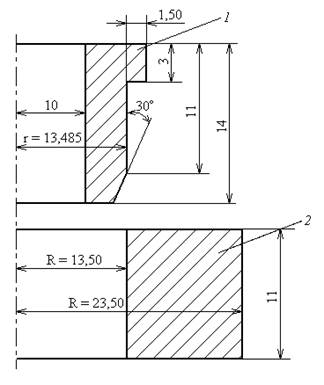
Рис. 2. Сечения сопрягаемых деталей 1 и 2
Между внешним диаметром детали 1 ивнутренним диаметром детали 2 имеется варьируемый в ходе исследования зазор ![]() , который изменялся в ходе компьютерного моделирования за счет изменения размера r = 13,485 (рис. 2).
, который изменялся в ходе компьютерного моделирования за счет изменения размера r = 13,485 (рис. 2).
Перед расчетом процесса сборки задают вес детали 1, вектор которого направлен вдоль оси OY с ускорением свободного падения ![]() , а также условия контакта между сопрягаемыми деталями. При этом были приняты следующие значения коэффициентов трения между деталями (сталь по стали): трения скольжения
, а также условия контакта между сопрягаемыми деталями. При этом были приняты следующие значения коэффициентов трения между деталями (сталь по стали): трения скольжения ![]() , трения покоя
, трения покоя ![]() [1].
[1].
Для задания вращения деталей 1 и 2, была экспериментально получена кривая разгона вращения устройства сборки. Для наблюдения за процессом вращения деталей была разработана система управления на базе микроконтроллера ATmega16. При вращении сепараторного диска c прорезью, прикрепленного к вращающемуся сборочному столику, установленный на основании фотодатчик меняет свой сигнал и посылает его на вход микроконтроллера с частотой, соответствующей частоте вращения сборочного столика. На LCD дисплее отображается количество прохождений прорези через фотодатчик, которое обновляется каждую секунду. Процесс разгона был снят на видеокамеру CanonPowerShotA570 IS, после чего данные были обработаны в программе Mathcad 14. На рис. 3 представлен график кривой разгона.
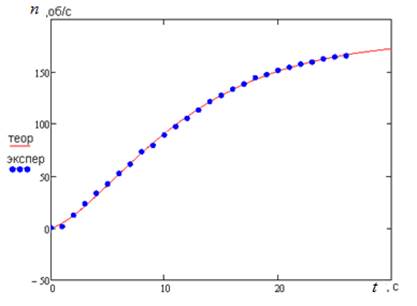
Рис. 3. Кривая разгона ротора установки
Теоретическое уравнение кривой разгона, полученное при использовании обобщенной регрессии в программе Mathcad 14, и заданное в модели SolidWorks для вращения деталей 1 и 2 имеет вид:
![]()
После того, как входные данные заданы, проведен расчет процесса сборки, с предварительно подключенным модулем SolidWorks Motion.
В результате расчетов получен визуальный процесс сборки и построены эпюры перемещения, частоты вращения.
На рис. 4 представлен момент окончания процесса сборки деталей.

Рис. 4. Окончание процесса сборки
Из расположения рисок на деталях (рисунок 4) видно, что относительного смещения деталей в плоскости вращения не наблюдается.
Для регистрации времени процесса сборки в нашем случае была использована зависимость перемещения центра тяжести детали 1 от времени, которая показана на рис. 5. Зависимость справедлива для начальных условий: ![]() .
.
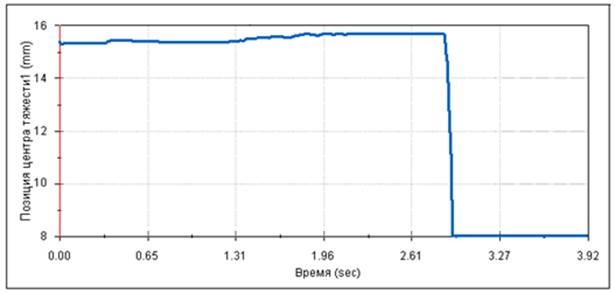
Рис. 5. Перемещение центра тяжести детали 1
Для более точного определения времени сборки полученная зависимость (рис. 5) конвертирован в таблицу значений CSV, которую можно открыть с помощью программы EXCEL. В таблице 1 приведен фрагмент полученной зависимости.
Таблица 1
Перемещение центра тяжести детали 1
|
Время, с |
Позиция центра тяжести, мм |
|
2,84532127399152 |
15,7016776745594 |
|
2,8566569845487 |
15,6484794562341 |
|
2,87001499536759 |
15,0315603571928 |
|
2,88 |
14,4595711738585 |
|
2,89097594956603 |
13,0899435016533 |
|
2,90233469872001 |
10,5801107160482 |
|
2,91239809241417 |
7,76948502667041 |
|
2,92 |
7,7588311053871 |
|
2,92574079963868 |
7,75738478551187 |
|
2,96 |
7,75761560143008 |
По полученным значениям определено время сборки с точностью до 0,02 с и в данном случае время сборки составило ![]() с.
с.
Изменяя зазор ![]() между сопрягаемыми поверхностями при прочих равных входных параметрах (угол наклона, коэффициенты трения, уравнение вращения) получены результаты, приведенные в таблице 2.
между сопрягаемыми поверхностями при прочих равных входных параметрах (угол наклона, коэффициенты трения, уравнение вращения) получены результаты, приведенные в таблице 2.
Таблица 2
Компьютерное моделирование процесса ротационной сборки
|
Зазор, s, мкм |
Время сборки, t, с |
Число оборотов в момент сборки n, об/с |
|
25 |
4,41 |
35,3 |
|
30 |
3,32 |
24,3 |
|
35 |
2,92 |
20,4 |
Из таблицы видно, что при увеличении зазора ![]() теоретическое время сборки уменьшается.
теоретическое время сборки уменьшается.
Еще одним варьируемым параметром является начальный угол![]() . перекоса между осями сопрягаемых деталей. Существует некоторое критическое значение угла
. перекоса между осями сопрягаемых деталей. Существует некоторое критическое значение угла ![]() наклона, при превышении которого собираемость деталей не гарантирована. Это значение угла наклона рассчитывается по формуле:
наклона, при превышении которого собираемость деталей не гарантирована. Это значение угла наклона рассчитывается по формуле:
![]()
где ![]() — отношение радиусов инерции относительно главных осей эллипсоида инерции детали 1.
— отношение радиусов инерции относительно главных осей эллипсоида инерции детали 1.
В рассматриваемом случае для детали 1 ![]() . Моделированием установлено (табл. 3), что величина начального угла перекоса осей сопрягаемых поверхностей практически не влияет на время сборки, что было подтверждено результатами экспериментального исследования.
. Моделированием установлено (табл. 3), что величина начального угла перекоса осей сопрягаемых поверхностей практически не влияет на время сборки, что было подтверждено результатами экспериментального исследования.
Таблица 3
Результаты моделирования при различных углах ![]() наклона осей сопрягаемых поверхностей
наклона осей сопрягаемых поверхностей
|
a, ° |
t, с |
n, об/с |
Расчетные данные |
|
7 |
3,28 |
23,9 |
|
|
9 |
3,08 |
21,9 |
|
|
11 |
3,27 |
23,8 |
|
|
13 |
3,54 |
26,4 |
|
|
15 |
3,32 |
24,3 |
|
|
17 |
3,19 |
23,0 |
|
|
19 |
3,25 |
23,6 |
|
|
21 |
3,14 |
22,5 |
|
|
23 |
3,41 |
25,1 |
|
|
25 |
3,39 |
25,0 |
Для проверки адекватности и возможности применения на практике разработанной компьютерной модели изготовлены экспериментальная установка для ротационной сборки и детали, математические модели которых были использованы при компьютерном моделировании (рис. 1). Причем деталь 1 изготовлена в трех экземплярах с разными диаметрами сопрягаемой поверхности — 26,975 мм, 26,970 мм и 26,965 мм, что соответствовало зазорам соединения в 25, 30 и 35 мкм. При этом сопрягаемые поверхности были выполнены с шероховатостью Ra 0,32.
На рис. 6 представлено относительное предварительное перед сборкой расположение сопрягаемых деталей.

Рис. 6. Расположение деталей перед сборкой: деталь 1, деталь 2, сборочный стол 3
Для каждой из трех деталей было проведено по 50 опытов, при этом собираемость узла — стопроцентная.
Все опыты фиксировались на видеокамеру, а затем с помощью программы SonyVegasPro 10.0 для обработки видео определялось время сборки деталей с точностью до 0,1 с. Полученные результаты приведены в таблице 4.
Таблица 4
Результаты экспериментов
|
Параметр |
s = 25 мкм |
s = 30 мкм |
s = 35 мкм |
|
— минимальное время сборки — максимальное время сборки — разброс значений времени — среднее время сборки — среднеквадратическое отклонение — дисперсия |
3,9 7 3,1 5,26 0,9047 0,8185 |
2,8 5,3 2,5 3,94 0,7233 0,5231 |
2,4 4,5 2,1 3,40 0,5461 0,2982 |
|
— теоретическое время сборки — разница между теоретическим и экспериментальным временем D, % |
4,41 19,18 |
3,32 18,55 |
2,92 16,37 |
Как можно заметить, результаты экспериментов отличаются от данных, полученных при помощи компьютерной модели на величину ![]() . Это обусловлено наличием погрешности измерений, а также параметрами реальной системы, такими как погрешности формы собираемых деталей, шероховатость и коэффициенты трения сопрягаемых поверхностей, вибрации.
. Это обусловлено наличием погрешности измерений, а также параметрами реальной системы, такими как погрешности формы собираемых деталей, шероховатость и коэффициенты трения сопрягаемых поверхностей, вибрации.
Все процессы моделирования сборки проводились с табличным значением коэффициента трения ![]() . На самом деле это значение для стальных поверхностей может варьироваться и достигать значения 0,3..0,35. Поэтому дополнительно проведено компьютерное моделирование с увеличенными значениями коэффициента трения. Данные моделирования приведены в таблице 5.
. На самом деле это значение для стальных поверхностей может варьироваться и достигать значения 0,3..0,35. Поэтому дополнительно проведено компьютерное моделирование с увеличенными значениями коэффициента трения. Данные моделирования приведены в таблице 5.
Таблица 5
Результаты дополнительных экспериментов
|
Параметр |
s = 25 мкм |
s = 30 мкм |
s = 35 мкм |
|
— среднее время сборки — теоретическое время сборки — коэффициент трения — разница между теоретическим и экспериментальным временем D, % |
5,26 4,81 0,25 9,27 |
3,94 3,78 0,24 4,13 |
3,40 3,39 0,27 0,24 |
Таким образом, расхождение практических результатов от компьютерной модели сведено к минимуму и не превышает 10 %, а для зазора ![]() практически отсутствует. Можно сделать вывод о том, что реальные значения коэффициентов трения для данных деталей находятся в диапазоне 0.24..0.27.
практически отсутствует. Можно сделать вывод о том, что реальные значения коэффициентов трения для данных деталей находятся в диапазоне 0.24..0.27.
Таким образом, разработанная компьютерная модель адекватна фактическому процессу сборки и может применяться для практического использования на стадии проектирования устройств ротационной сборки цилиндрических деталей.
Литература:
1. Анурьев В. И. Справочник конструктора-машиностроителя: В 3-х т. Т. 1. — 5-е изд., перераб. и доп. — М.: Машиностроение, 1979. — 728 с., ил.
2. Пат. РФ № 2239735. Устройство для сборки роликовых подшипников/ М. Г. Кристаль, Е. В. Стегачев, А. В. Широкий//Б.И. — 2004. — № 31.
3. Пат. РФ № 2423217. Способ сборки деталей типа вал-втулка/ М. Г. Кристаль, С. С. Серов, Т. В. Безрукова//Б.И. — 2011. — № 19.







