Введение
Речевой звук — звук, образуемый произносительным аппаратом человека с целью языкового общения. К произносительному аппарату относятся: глотка, ротовая полость с языком, лёгкие, носовая полость, губы, зубы.
В целом звуки речи подразделяются на шумы и тоны: тоны в речи возникают в результате колебания голосовых складок; шумы образуются в результате непериодических колебаний выходящей из лёгких струи воздуха. Тонами являются обычно гласные; почти же все глухие согласные относятся к шумам. Звонкие согласные образуются путём слияния шумов и тонов. Шумы и тоны исследуются по их высоте, тембру, силе и многим другим характеристикам. [1]
В данной статье рассматриваются существующие математические модели речевых трактов, их преимущества, недостатки и ограничения. Исходя из результатов анализа, будут обоснованы причины для расчета и разработки новой математической модели речевого аппарата человека. Будут подчеркнуты недостатки существующих моделей.
Существующие модели речевого тракта
На данный момент наиболее популярной является одна модель речевого тракта. Модель базируется на том, что одним из источников образования звуков является голосовой источник, который возникает при колебании голосовых связок. Этот источник участвует в образовании нескольких групп звуков, и по степени участия голосового источника звуки делятся на гласные и согласные. Рассмотрим подробнее данную модель сегмента речевого сигнала, применительно к задачам анализа синтеза речи. Физическая модель образования речи показана на рис. 1.
Входной сигнал x(t) поступает от голосовых связок (природный генератор колебаний), проходит через N-е количество параллельно соединенных резонаторов (характеризующих форму речевого тракта), таким образом, на выходе формируется определенный произносимый вокализованный речевой сегмент y(t).
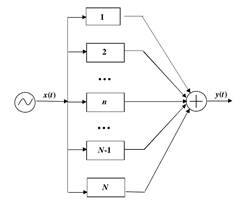
Рис. 1 Модель речевого сигнала для вокализованного сегмента речи
Известно, что гласные звуки представляют собой квазипериодические колебания, вызванные действия голосовых связок [2], таким образом, целесообразно использовать гармонические математические модели, адекватно описывающие данные сегменты речи. [3]
Экспериментальным путем было установлено, что для вокализованного сегмента речи, амплитуды на частотах основного тона и обертонов речевого сигнала существенно влияют на «фонетический смысл» гласных звуков. [3]
В данной модели сигнал источник (голосовых связок) представлен в виде сложного периодического колебания, состоящего из набора гармоник с произвольными амплитудами и начальными фазами которое проходит через речевой тракт, представляющий собой несколько параллельно соединенных резонаторов.
Методом разделения переменных можно получить дифференциальные уравнения второго порядка, характеризующие временную зависимость звукового поля при формировании вокализованного речевого сигнала. [4]
Рассмотрим полученную математическую модель вокализованного сегмента речи y(t), являющуюся решением дифференциального уравнения, которое описывает прохождение периодических колебаний от источника в виде голосовых связок (т. е. полигармонического сигнала или нескольких гармоник ряда Фурье) через систему параллельных резонаторов с затуханием:
![]() (1)
(1)
где ?n = 2πFn; Fn — n-я формантная частота; ω0 = 2πf0; f0 — частота основного тона, an — коэффициент затухания n-го резонатора; bi и φi — соответственно амплитудные коэффициенты и начальные фазы; характеризующие сигнал генератора, т. е. сигнал, формируемый голосовыми связками; N — количество резонаторов; L — количество гармоник сигнала генератора; Сn — коэффициенты, характеризующие распределение воздушного потока (от сигнала источника) между резонаторами.
Для уравнения (1), применив принцип суперпозиции, получим следующие дифференциальные уравнения:
![]() (2)
(2)
Решение данных дифференциальных уравнений yn,l(t) дает математическую модель речевого сигнала y(t) для вокализованных сегментов речи:
![]() (3)
(3)
Решение уравнения (1) в общем виде:
![]() (4)
(4)
Следует отметить, что общие решения неоднородных дифференциальных уравнений (2) представляют в виде суммы общих решений однородных дифференциальных уравнений и частных решений неоднородных дифференциальных уравнений:
![]() (5)
(5)
Неопределенные коэффициенты можно получить для задачи Коши.
Дифференциальное уравнение при учете частотной модуляции имеет вид:
![]() (6)
(6)
Для обеспечения условия соблюдения максимума мгновенного значения частоты основного тона, в середине временного интервала (длительность вокализованного сегмента) предполагается ψ0 = π/2, в результате дифференциальное уравнение приобретает вид:
![]() (7)
(7)
Для решения дифференциального уравнения (7) с целью получения математической модели y(t) представим l-e слагаемое в правой части выражения (7), используя разложение в ряд по функциям Бесселя. [5]
Анализ данной математической модели речевого тракта
Данная модель в полной мере описывает процесс образований вокализованного сигнала, учитывая наличие резонаторов в речевом аппарате человека. Позволяет построить сигналы, подобные реальным речевым сигналам. Амплитудно-частотный спектр, полученный по результатам моделирования также подобен спектру реального сигнала.
К сожалению, данная математическая модель не учитывает функции многих резонаторов, находящихся ниже голосовых связок, которые имеют большое влияние на амплитуду основного тона и гармоник.
Данная модель, к сожалению, не пригодна и для описания тувинского горлового пения, но на основе этой модели можно разработать модель, которая в полной мере будет способна описать процесс образования вокала при использовании резонаторов, находящихся ниже голосовых связок.
Не учтены весьма важные характеристики вокала и певческие характеристики, что делает данную модель не актуальной при моделировании певческого голоса.
Для описания всех процессов, возникающих при образовании голоса, необходимо учитывать акустические, физиологические, психологические закономерности образования и восприятия певческого голоса, описанные в работах профессора Владимира Петровича Морозова, разработавшего резонансную теорию пения. В отличии от существовавших ранее теорий, качающихся роли голосовых складок и дыхания, данная теория изучает функции резонаторов, как наименее изученную часть голосового аппарата во взаимодействии с работой гортани и дыхания. Данная теория имеет практическое назначение, как с научной точки зрения, так и с точки зрения музыкальной акустики и вокальной педагогики.
Новизна термина «резонансное пение» требует его пояснения. Строго говоря, «нерезонансного» пения, также как и обычной «нерезонансной» речи не бывает, так как во всех случаях резонаторы голосового аппарата участвуют в формировании речевых и певческих звуков. Вместе с тем, роль резонаторов в голосовом аппарате как усилителей голоса и преобразователей тембра может быть различной: от минимальной до весьма значительной, в зависимости, во-первых, от природных особенностей строения резонаторов, а во вторых, от особенностей их использования, точнее — от характера и степени активизации резонансной системы поющим, что достигается особенностями сонастройки резонаторов, то есть от техники голосообразования, включая и правильную организацию певческого диафрагматического дыхания.
Резонансная теория пения является развитием этих, общепризнанных мировой наукой идей о резонансных механизмах речеобразования, но уже применительно к специфике работы певческого голосового аппарата, служащего для формирования не обычных речевых звуков, но специфической певческой вокальной речи, то есть эмоционально-эстетических особенностей певческого голоса, особого певческого тембра, вибрато и др. Это связано с особенностями работы голосового аппарата певца, прежде всего — резонаторов, но не только ротоглоточного, но и грудного (трахея, бронхи), что и отражается в формантной структуре спектра голоса. [6]
Выводы
В результате анализа актуальных на данных момент математических моделей голосовых аппаратов сделал вывод, что данные математические модели не в полной мере способны описать образование певческого голоса и некоторых его специфических подвидов, поскольку нынешние модели имеют достаточно много ограничение и не учитывают функции многих резонаторов.
Для более качественного описания процесса голосообразования и образования певческого голоса необходимо учитывать больше критериев, описанных в теории резонансного пения.
Данный анализ проведен с целью дальнейшей разработки математической модели, способной в полной мере описать процесс образования певческого вокала и для разработки математической модели описывающей процесс образования более специфических видов вокала, как тувинское горловое пение, фальцет, и им подобные. Данные виды вокала невозможно описать без учета резонанса дыхательных путей, легких и мышц, которые находятся в области живота и грудной клетки.
Литература
1. Речевой звук — Википедия. http://ru.wikipedia.org/wiki/ %D0 %A0 %D0 %B5 %D1 %87 %D0 %B5 %D0 %B2 %D0 %BE %D0 %B9_ %D0 %B7 %D0 %B2 %D1 %83 %D0 %BA
2. Золотарев В. В., Овечкин Г. В. Помехоустойчивое кодирование. Методы и алгоритмы: справочник / под ред. чл.-кор. РАН Ю. Б. Зубарева. — М.: Горячая линия — Телеком, 2004. — 126 с.
3. Голубинский А.Н, Гущина А. А. Анализ и синтез гласных звуков на основе математической модели в виде импульса колебания с амплитудно-частотной модуляцией со сложным несущим сигналом // наука и современность: сборник материалов Международной научно-практической конференции. — Новосибирск, 2012. — С. 23–28.
4. Баскаков С. И. Радиотехнические цепи и сигналы: учеб. Для вузов по спец. «Радиотехника». — М: Высш. шк. 1983. — 536.
5. Голубинский А.Н, Гущина А. А. Математическая модель вокализованных сегментов речевого сигнала, основанная на модели речевого тракта
6. Резонансная теория пения — Википедия. http://ru.wikipedia.org/wiki/ %D0 %A0 %D0 %B5 %D0 %B7 %D0 %BE %D0 %BD %D0 %B0 %D0 %BD %D1 %81 %D0 %BD %D0 %B0 %D1 %8F_ %D1 %82 %D0 %B5 %D0 %BE %D1 %80 %D0 %B8 %D1 %8F_ %D0 %BF %D0 %B5 %D0 %BD %D0 %B8 %D1 %8F







