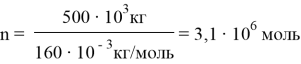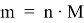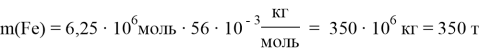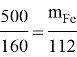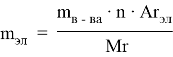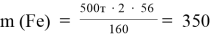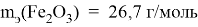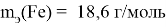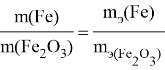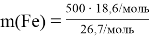В данной статье рассмотрены способы решения стандартных (типовых) задач, в том числе и элементарных. Методика ориентирована в основном для школьников, впервые приступающих к решению задач повышенной сложности.
Статья посвящена способам решения задач по химии, обеспечивая необходимую базу для дальнейшей работы. Анализ решений и ответы на задачи приводятся непосредственно вслед за условием каждого способа, что также облегчает восприятие материала.
Ключевые слова : химия, решение задач, условие задачи, изучение химии, способы решения, методика, эффективность обучения.
При решении задач по химии часто применяется только один традиционный метод, что может затруднять развитие мышления учащихся. Этот подход не учитывает индивидуальные особенности учеников и ограничивает их действия только действиями преподавателя. Однако существуют разнообразные способы решения расчетных задач, отличающиеся по уникальности, трудоемкости и другим характеристикам. Более того, одна и та же задача может быть решена несколькими способами.
Используя разные методы, ученики смогут самостоятельно находить выход из ситуаций. Решая задачи разными способами, можно развивать мышление и действия учащихся [3]. Давайте продемонстрируем примеры различных методов расчета. Покажем на примере, как выполнить расчет разными способами.
Задание : Партия руды массой 500 тонн, содержащая гематит
(Fe 2 O 3 ), поступила на завод. Определите количество железа, которое можно извлечь из этой руды.
В этом задании не говорится о химическом процессе. Массу железа в руде мы можем определить по формуле. По формуле вещества в 1 моль Fe 2 О 3 содержится 2 моль атомов Fe. Если мы удвоим количество молей руды, то и количество молей железа также yдвоится. Между массой руды и массой жeлeза существует прямая пропорциональная зависимость. Используя данную прямyю зависимость, попробуем рeшить задачy разными методами. Рассмотрим восемь различных подходов к решению.
Сп о с о б № 1. Стехиометрический расчет
|
Дано: |
Решение: |
|
m(Fe 2 O 3 ) = 500 т |
Определение модекулярной массы гематита: m = n ∙ M M(Fe2O3) = 160 г/моль M(Fe) = 56 г/моль m(Fe2O3) = 1 моль ∙ 160 г/моль = 160 г Доля железа в Fe2O3: m(Fe) = 2 моль ∙ 56 г/моль = 112 г m(Fe) m( Fe 2 O 3 ) = 112 160 = 1 1,43 Масса железа в гематите будет на 1,43 раза меньше. Предполагая, что вся руда состоит только из гематита, масса железа: m(Fe) = 500 т 1,43 = 350 т |
|
m(Fe) -? (т) |
|
|
Ответ: В 500 т Fe2O3 сoдeржитcя 350 т Fe |
Cпocoб № 2. Сравнение масс материи
Этим способом oпрeдeляют массы веществ по формуле или уравнению реакций [4].
|
Дано: |
Решение: |
|
m(Fe 2 O 3 ) = 500 т |
Определите массу гематита (Fe2O3) и железа в нём. В 1 моль Fe2O3 содержится 2 моль Fe; M(Fe2O3) = 160 г/моль M(Fe) = 56 г/моль m = n∙M m(Fe2O3) = 1 моль ∙ 160 г/моль = 160 г Масса железа в одной молекуле Fe2O3: m(Fe) = 2 моль ∙ 56 г/моль = 112 г Рассчитайте процентное содержание железа в Fe2O3. Доля железа в Fe2O3 = (Масса железа / Молекулярная масса Fe2O3) ∙ 100 % = 112: 160 = 70 % Рассчитайте массу железа в 500 тоннах руды: m(Fe2O3) = 500 тонн = 500 ∙ 106 г m(Fe) = 500 ∙ 106 ∙ 0,7 = 350 т |
|
m(Fe) -? (т) |
|
|
Ответ: В 500 т Fe 2 O 3 содержится 350 т Fe. |
Способ № 3. Р ac ч e т c использованием понятия «м o ль»
Для более глубокого освоения понятий «моль» и «молярная масса» полезно решать задачи, используя эти термины в численных расчетах.
С помощью таких методов студенты учатся структурировать свои мысли, экономят время, лучше понимают суть химических процессов и более детально изучают количественные и качественные аспекты химических уравнений и формул [2].
|
Дано: |
Решение: |
|
m(Fe 2 O 3 ) = 500 т |
M(Fe 2 O 3 ) = 160 ∙ 10 –3 кг/моль M(Fe) = 56 ∙ 10 –3 кг/моль Пo формуле вещества в 1 моль Fe 2 O 3 содержится 2 моль атомов Fe. Путем применения формулы m = n / M, мы вычисляем количество железа в 500 т руды.
3,125 ∙ 10 6 моль Fe 2 O 3 содержит 6,25 ∙ 10 6 моль Fe.
Для определения массы вещества можно применить следующую формулу:
|
|
m(Fe) -? (т) |
|
|
Ответ: В 500 т Fe 2 O 3 содержится 350 т Fe. |
Способ № 4. Метод пропорций
При составлении отчетов данным методом рекомендуется придерживаться следующей последовательности действий [1]:
- Определить пропорциональную зависимость.
- Составление пропорцию.
- Провести расчет на основе пропорции.
|
Дано: |
Решение: |
|
m(Fe 2 O 3 ) = 500 т |
M(Fe 2 O 3 ) = 160 кг/кмоль M(Fe 2 O 3 ) = 56 кг/кмоль m = n ∙ M m(Fe 2 O 3 ) = 1 моль ∙ 160 ∙ 10 –3 = 160 ∙ 10 –3 кг m(Fe) = 2 моль ∙ 56 ∙ 10 –3 = 112 ∙ 10 –3 кг По формуле вещества в 1 моль Fe 2 O 3 содержится 2 моль атомов Fe. Можно установить пропорциональную зависимость: в 160 ∙ 10 –3 кг Fe 2 O 3 содержится 112 ∙ 10 –3 кг Fe, следовательно в 500 т Fe 2 O 3 будет содержаться m т Fe.
Далее можно рассчитать неизвестное значение: m(Fe) = 500 ∙ 112: 160 = 350 т |
|
m(Fe) -? (т) |
|
|
Ответ: В 500 т Fe 2 O 3 содержится 350 т Fe |
Способ № 5. Расчет по алгебраическим формулам
Можно решать химические задачи, применяя алгебраические формулы [1]. Например, мы выполняем расчеты согласно следующим формулам.
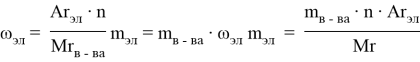
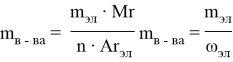
Чтобы определить массу вещества по известной массе элемента в нем, необходимо умножить массу элемента на относительную молекулярную массу вещества и разделить на произведение относительной атомной массы элемента и на индекс при знаке элемента, указанной в формуле этого вещества.
|
Дано: |
Решение: |
|
m(Fe 2 O 3 ) = 500 т |
Решим задачу подставив данные в формулу.
|
|
m(Fe) -? (т) |
|
|
Ответ: В 500 т Fe 2 O 3 содержится 350 т Fe. |
Способ № 6. Применение закона эквивалентов
Учитель должен представить ученикам понятие эквивалентности и объяснить основу закона эквивалентности. Необходимо объяснить правила определения эквивалентности как простых, так и сложных веществ. Важно помнить, что в процессе решения задач следует вычислять не молярные массы, а эквивалентные массы [2].
На основании закона эквивалентов:
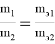
где m 1 и m 2 — масса простых и сложных веществ;
m э1 и m э2 — эквивалентные массы этих веществ.
|
Дано: |
Решение: |
|
m(Fe 2 O 3 ) = 500 т |
Подставив эти данные в формулу, мы можем найти массу железа:
|
|
m(Fe) -?(т) |
|
|
Ответ: В 500 т Fe 2 O 3 содержится 350 т Fe. |
Способ № 7. Приведение к единице [4]
|
Дано: |
Решение: |
|
m(Fe 2 O 3 ) = 500 т |
M(Fe 2 O 3 ) = 160 г/моль M(Fe) = 56 г/моль m = n ∙M m(Fe) =2 моль ∙ 56 г/моль = 112 г M(Fe 2 O 3 ) = 1 моль ∙ 160 г/моль = 160 Если в 160 г Fe 2 O 3 содержится 112 г Fe, тогда в 1 г Fe 2 O 3 будет содержаться в 160 раза меньше, то есть 112:160 г. В 500 т Fe 2 O 3 железа будет больше в 500 ∙ 10 6 раз, чем в 1 г. m(Fe) = 112: 160 ∙ 500 ∙ 10 6 = 350 ∙ 10 6 кг = 350 т |
|
m(Fe) -? (т) |
|
|
Ответ: В 500 т Fe 2 O 3 содержится 350 т Fe. |
Способ № 8. Использование коэффициентов пропорциональности
В курсе алгебры есть формула, связанная с понятием пропорциональности:
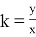
А коэффициент пропорциональности в курсе химии определяется по следующей формуле
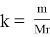
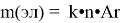
|
Дано: |
Решение: |
|
m(Fe 2 O 3 ) = 500 т |
Mr (Fe2O3) = 160 Ar (Fe)= 56 k= m Mr k = 500: 160 = 3,125 m(эл)= k•n•Ar m(Fe) = 3,125 ∙ 2 ∙ 56 = 350 т |
|
m(Fe) -? (т) |
|
|
Ответ: В 500 т Fe 2 O 3 содержится 350 т Fe. |
Во всех подходах количество железа, которое можно извлечь из 500 тонн руды, содержащий гематит, составляет 350 тонн. При прохождении педагогической практики анализ школьных программ по химии показал, что уровень сложности расчетных задач очень низкий. Также не выделено отдельного времени на обучение решению задач, что приводит к тому, что ученики успевают освоить лишь теорию. В учебниках по химии очень мало примеров решения задач или они практически отсутствуют. Данные способы будут полезны учителю в школе. Они могут помочь разнообразить процесс, сделать занятия более интересными и понятными для учеников. Предоставление примеров решения задач поможет стимулировать учеников активному участию и развитию аналитических навыков. Такой подход может также способствовать более глубокому пониманию химических процессов и их применение на практике [4].
Литература:
- И. К. Цитович, Методика решения расчетных задач по химии: Кн. для учителя / П. Н. Протасов — 4-е изд., перераб. — М.: Просвещение, 1983.–127 с.
- Ә. Шолақтегі, Жалпы химиядан есептер шығару үлгілері және есептер жинағы / Алматы: «Эверо», 2016. — 116 б.
- В. К. Николаенко, Сборник задач по химии повышенной трудности: учебное пособие для средних учебных заведений / Под ред. проф. Г. В. Лисичкина. — М.: РОСТ, МИРОС, 1996. — 192 с.
- Е. В. Лагуткина, Методика решения задач по химии: учебно-методическое пособие / И. Б. Катраков — Барнаул: Изд-во Алт. ун-та, 2014. — 44 с.