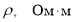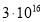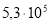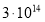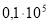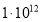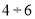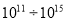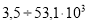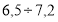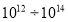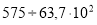В статье рассматриваются слабопроводящие среды в конденсаторах, оценивается изменение величины тока утечки.
Ключевые слова : конденсатор, слабопроводящая среда, ток утечки
Физика как фундаментальная точная наука способствует качественному освоению курсантами специальных дисциплин (автоматика и управление,комплексы авиационного и радиоэлектронного оборудования, радиотехника и т. д.), формированию научного мышления и самостоятельному совершенствованию в будущей профессиональной деятельности военных инженеров.
Обучение физике в военном вузе предусматривает профессиональную направленность содержания учебного материала, применяемых приемов и технологий, формирующих требуемые компетенции.
Современные профессионально-ориентированные образовательные технологии позволяют создать педагогическое пространство, структурные элементы которого обеспечивают достижение качественных результатов обучения при взаимодействии обучающегося и преподавателя [1, c.39] на аудиторных занятиях и в рамках работы военно-научного общества (ВНО).
Работа курсантов в ВНО является эффективным средством формирования, углубления и реализации научных знаний при решении проблемных задач, например, электродинамики. Законы этого раздела физики применяются в радиотехнике, автоматике для получения кратковременных импульсов с помощью схем, содержащих конденсаторы.
Конструктивно конденсаторы изготовляют в виде токопроводящих обкладок, разделенных диэлектриком. Цилиндрический конденсатор состоит из двух соосных тонкостенных цилиндрических обкладок, разделенных цилиндрическим слоем диэлектрика. Если внутреннюю обкладку подобного устройства зарядить, внешнюю — заземлить, то, пренебрегая краевыми эффектами, его поле будет радиально-симметричным и сосредоточенным между цилиндрическими обкладками.
Используя теорему Остроградского-Гаусса, определим емкость цилиндрического конденсатора
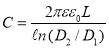
где
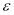
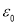
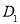
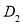
Если конденсатор оставить разомкнутым, то будет происходить саморазряд конденсатора за счет тока утечки через сопротивление изоляции. Ток утечки является одним из критических факторов применения конденсаторов. Он обусловлен наличием в диэлектрике свободных носителей заряда и зависит от диэлектрической проницаемости среды, температуры окружающей среды, температуры хранения (обычно она не должна превышать 125 0 С), приложенного напряжения, величина которого не превосходит значение номинального напряжения.
Определим закон изменения силы тока утечки с течением времени.
Начнем с рассмотрения однородного участка электрической цепи, представляющего физическую систему, в которой электрическое поле является причиной упорядоченного направленного движения свободных зарядов слабопроводящей среды. В этой среде будем пренебрегать изменением мгновенных значений силы тока, разности потенциалов. Следовательно, можно использовать закон Ома в дифференциальной и интегральной формах.
Для однородного участка цепи, полное сопротивление которого равно R , запишем закон Ома в интегральной форме
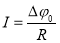
Элементарное сопротивление тонкостенного цилиндрического слоя высотой L , толщиной dr и радиусом r определяется выражением
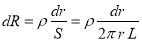
где S — площадь поверхности,
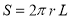
Чтобы найти полное противление однородного участка следует проинтегрировать равенство (3) в пределах изменения радиусов
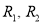
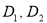
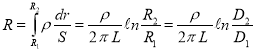
Подставляя выражение (4) в формулу (2), получим
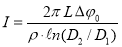
Выражение (5) справедливо, если
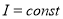
Условие постоянства разности потенциалов (
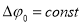
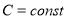
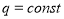
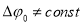
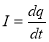
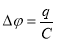
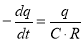
Знак минус в равенстве (6) означает уменьшение тока утечки.
Разделив переменные в формуле (6) и проинтегрировав полученное выражение, запишем
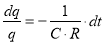
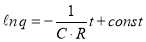
Если
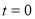
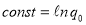
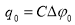
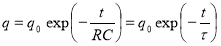
где
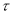
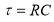
Если в равенстве (9)
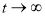
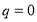
Используя выражения (1) и (4), определим постоянную релаксации
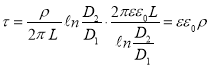
Изменением величин мгновенных значений силы тока, разности потенциалов на обкладках конденсатора, заряда можно пренебречь, если время релаксации будет велико. Следовательно, можно говорить о слабопроводящей среде. В таблице 1 в сравнении даны характеристики ряда диэлектриков: диэлектрическая проницаемость
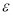
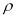
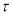
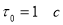
Таблица 1
Диэлектрическая проницаемость ε, удельное сопротивление ρ, время релаксации τ ряда диэлектриков и условная оценка среды (слабопроводящая СП, неслабопроводящая НСП)
|
Вещество |
|
|
|
Оценка среды |
|
парафин |
2 |
|
|
СП |
|
кварц |
4,4 |
|
|
СП |
|
кварц |
4,7 |
|
42 |
СП |
|
слюда (мусковит) |
|
|
|
СП |
|
слюда (флогопит) |
|
|
|
СП |
|
мрамор |
8,3 |
|
|
НСП |
|
пятиокись тантала |
27 |
|
|
НСП |
Как видно из таблицы 1 парафин, оба сорта кварца, оба сорта слюды (мусковит) и слюды (флогопит) можно считать слабопроводящими средами, т. к. их время релаксации значительно превосходит время наблюдения.
Используя выражения (9) и (10), найдем закон изменения тока утечки в конденсаторе с течением времени
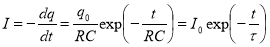
Формула (4) дает начальную (максимальную) величину тока утечки.
Рассчитаем ток утечки для цилиндрического конденсатора, у которого диаметр его внутреннего цилиндра
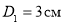
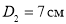
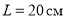
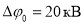
Ток утечки определяется через 1–5 минут после включения конденсатора и подачи номинального напряжения на обкладки конденсатора.
В таблице 2 представлены емкость конденсатора C, диэлектрик в котором является слабопроводящей средой, и величина тока утечки I через 5 минут после подачи напряжения.
Таблица 2
Емкость конденсатора С , ток утечки I
|
Вещество |
|
|
I , пА |
|
парафин |
2 |
9,8 |
0,9 |
|
кварц |
4,4 |
21,6 |
92,3 |
|
слюда (мусковит) |
6 |
29,4 |
2,9 |
|
слюда (флогопит) |
|
35,3 |
261,7 |
Как видно из таблицы 2 величина тока утечки в конденсаторах с рассмотренными диэлектриками невелика.
Таким образом, в ходе работы в рамках ВНО мы проанализировали понятие «слабопроводящая среда» и оценили изменение тока утечки в ней.
Литература:
- Ваганова О. И., Абрамова Н. С., Максимова К. А. Профессионально- ориентированные технологии // Балтийский гуманитарный журнал. — 2019. — Т.8. — № 4(29).— С. 38–41.