Встатье рассматриваются преимущества искусственных нейронных сетей в задачах дешифрирования объектов дистанционного зондирования земли. Проведен анализ метода обучения обратного распространения ошибки, отличающийся от известных тем, что применение его для решения задач дешифрирования объектов, дистанционного зондирования земли, уменьшает время обнаружения и повышает вероятность распознавания объектов. Представлен пример автоматического решения задачи дешифрирования объектов на аэроснимках с помощью алгоритма нейронной сети R-CNN, обученной методом обратного распространения ошибки. Проведен анализ сравнения решение задачи дешифрирования искусственными нейронными сетями и оператором-дешифровщиком.
Ключевые слова: искусственный интеллект, распознавание, дешифрирование, аэроснимок, алгоритм.
Введение. Анализ процесса летных испытаний (ЛИ) при решении задач дешифрирования объектов дистанционного зондирования земли (ДЗЗ) показывает, что сроки проведения испытаний продолжают увеличиваться, а достоверность полученных в испытаниях оценок остается недостаточной. Задача дешифрирования объектов ВзР на аэроснимках является одной из основных задач ВзР. Одним из путей решения вопроса является внедрение в процесс испытаний алгоритмов искусственных нейронных сетей (ИНС).
Технологии ИНС позволяют существенно расширить возможности распознавания объектов ДЗЗ на аэроснимках, полученных оптико-электронными системами пилотируемых и беспилотных летательных аппаратов. ИНС позволяют в автоматическом режиме с высокой достоверностью дешифрировать объекты ДЗЗ на аэроснимках, что повышает оперативность решения задач дешифрирования в том числе при проведении летных испытаний.
Сложность дешифрирования значительно возрастает из-за высокой изменчивости изображений объектов, обусловленной множественностью цветов, форм, ракурсов объектов, а также влиянием условий аэросьемки, внешней освещенности, атмосферных явлений (рассеяние, поглощение, рефракция, турбулентность), дестабилизирующих факторов полета. Учет этих факторов требует обученности алгоритмов ИНС к различным условиям и изменениям в окружающей среде под конкретную задачу.
Целью данной статьи является анализ применения метода обучения ИНС обратного распространения ошибки для повышения эффективности решения задач дешифрирования объектов ДЗЗ.
Основная часть. Обучение — процесс, в котором свободные параметры ИНС настраиваются посредством моделирования среды, в которую эта ИНС встроена [1]. Не существует универсального алгоритма обучения для всех архитектур ИНС, существует лишь набор средств, представленный множеством алгоритмов обучения, каждый из которых имеет свои достоинства. Алгоритмы обучения отличаются друг от друга способом настройки синаптических связей нейронов, поэтому для решения конкретной задачи нужно выбирать свой алгоритм обучения. Алгоритм обучения ИНС для решения задач дешифрирования объектов ВзР на аэроснимках представлен на рисунке 1.

Рис. 1. Алгоритм обучения ИНС
Для решения задачи распознавания объектов на аэроснимках требуется обучение ИНС по специально подготовленному набору данных, который содержит изображения всех классов распознаваемых объектов, сгруппированных в соответствующие разделы. Такой тип данных носит название датасет [2]. Процесс обучения ИНС представляет собой сложный процесс обработки данных, который включает в себя последовательное предъявление данных на вход ИНС и сравнение выходных данных с их истинным значением, после чего вносится коррекция весовых коэффициентов нейронов в сторону уменьшения ошибки выходных данных. Этот процесс производится многократно с использованием данных из датасета. Для решения задач дешифрирования объектов ДЗЗ используются многослойные ИНС. Обучение ИНС происходит методом обратного распространения ошибки, основная идея которого состоит в распространение сигналов ошибки от выходов ИНС к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы [3]. Состоит из двух этапов:
а) Прямое распространение — процесс прохождения данных через ИНС от входного слоя к выходному слою [3]. (рисунок 2) [4].
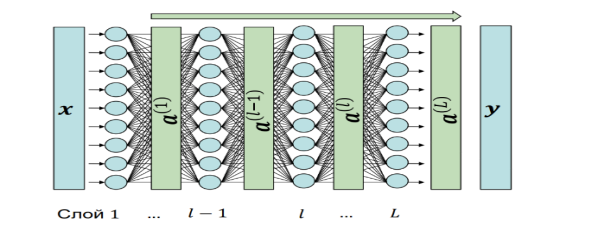
Рис. 2. Прямое распространение метода обратного распространения ошибки
Прямое распространение включает в себя следующие процессы:
- Объект ДЗЗ подается на вход ИНС.
- Последовательно вычисляются выходные сигналы a l для каждого слоя ИНС.
Выходные сигналы a l рассчитываются по формуле: [4]

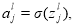
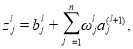
где
a
j
l
—
выходные сигналы ИНС;
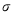
3. Вычисляется мера влияния нейронов выходного слоя на ошибку работы ИНС. Мера влияния — показатель того, насколько изменение активации конкретного нейрона (или его параметров, таких как вес и смещение) влияет на общую ошибку или функцию потерь алгоритма ИНС. Данное понятие используется для оценки значимости каждого нейрона в контексте обучения.
Мера влияния одного нейрона на работу ИНС рассчитывается по формуле: [4]
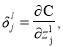

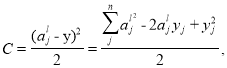
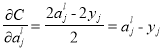
где
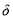
Воспользуемся правилом дифференцирование сложной функции:
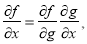
где, f, g, x — функции.
Мера влияния нейронов выходного слоя на ошибку ИНС с учетом правила дифференцирования сложной функции рассчитывается по формуле [4]
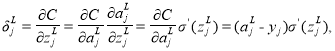
где L — выходной слой ИНС.
б) Обратное распространение — процесс прохождения данных через ИНС от выходного слоя к входному слою (рисунок 3) [4].
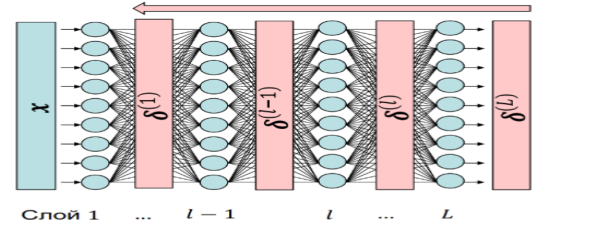
Рис. 3. Обратное распространение метода обратного распространения ошибки
Обратное распространение включает в себя следующие процессы:
1. Вычисляется в обратном порядке мера влияния нейронов на ошибку для каждого слоя.
Для расчета меры влияния на ошибку для каждого слоя необходимо рассчитать активационный потенциал для каждого слоя ИНС по формуле: [4]
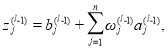
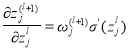
Мера влияния одного нейрона на ошибку ИНС рассчитывается по формуле 3. Воспользуемся правилом дифференцирования для многих переменных:
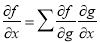
Мера влияния нейронов на ошибку ИНС для каждого слоя в обратном направлении рассчитывается по формуле: [4]
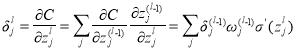
2. Вычисляется градиент по смещению и по весам. Градиенты по весу и смещению представляют собой производные функции потерь по параметрам ИНС (весам и смещениям).
Градиент по смещению рассчитывается по формуле: [4]
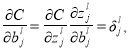
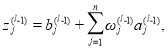
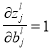
Градиент по весам рассчитывается по формуле: [4]
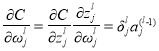
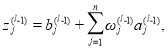
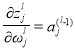
3. Корректировка веса и смещения ИНС. На данном этапе происходит модификация синаптических связей между нейронами разных слоев, за счет изменения параметров веса и смещения в соответствии с формулами: [5]
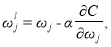
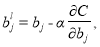
где α — скорость обучения ИНС.
Работа данного метода обучения обратного распространения ошибки продолжается до тех пор, пока не перестанут изменяться параметры веса и смещения (рисунок 4).
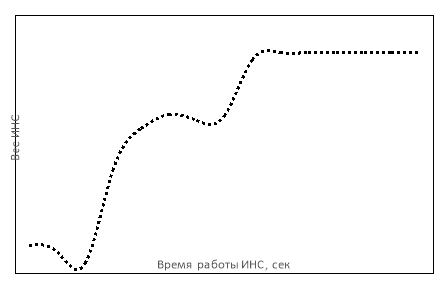
Рис. 4. График зависимости веса ИНС от времени работы
В данном примере работы ИНС R-CNN в момент времени равному 5,5 секунды перестают изменяться весовые коэффициенты ИНС, это означает что данная сеть обучена.
Результаты и их обсуждение
Рассмотрим работу ИНС R-CNN, обученной методом обратного распространения ошибки для решения задач дешифрирования объектов ДЗЗ на аэроснимках. Пример работы алгоритма ИНС R-CNN представлен на рисунке 5.
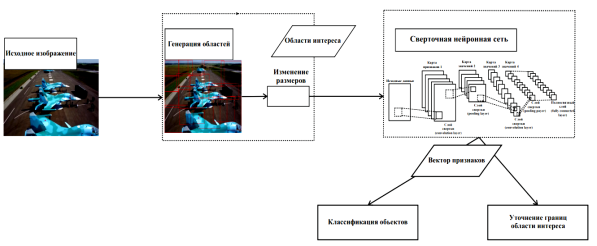
Рис. 5. Алгоритм работы ИНС R-CNN
Обучение ИНС происходило на выборке, состоящей из четырех классов: дороги, самолеты, автомобили, БПЛА различных типов. Общее количество образцов изображений для обучающей выборки составило около 10000. Образцы обучающей выборки представлены на рисунке 6.

Рис. 6. Образцы обучающей выборки
Распознавание объектов на изображении с использованием ИНС R-CNN состоит из следующих этапов:
– обучение ИНС R-CNN методом обратного распространения ошибки для решения задач дешифрирования объектов ДЗЗ;
– генерация областей интереса, предположительно содержащих в себе искомые объекты (обычно до 2000 возможных областей) с использованием алгоритма ИНСR-CNN;
– формирование карты признаков для исходного изображения;
– классификация объекта для каждой области интереса.
Пример работы ИНС R-CNN, обученной методом обратного распространения ошибки представлен на рисунке 7.
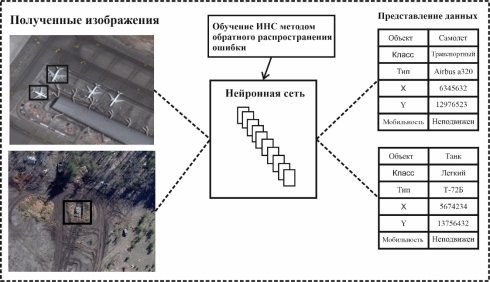
Рис. 7. Дешифрирование объектов ДЗЗ с использованием ИНС R-CNN, обученной методом обратного распространения ошибки
Вероятность распознавания объекта ДЗЗ и время представлены в таблице 1. Графики зависимости вероятности распознавания и времени от эпохи обучения ИНС представлены на рисунке 8.
Таблица 1
Результаты работы ИНС R - CNN , обученной методом обратного распространения ошибки
|
Способ дешифрирования |
Эпохи обучения |
Объект |
Сложность изображения |
Вероятность распознавания |
Время распознавания , c ек |
|
ИНС R-CNN с методом обучения обратного распространения ошибки |
50 |
самолет |
высокая |
0,682 |
4,22 |
|
100 |
0,711 |
3,98 |
|||
|
150 |
0,725 |
3,66 |
|||
|
200 |
0,766 |
2,87 |
|||
|
250 |
0,812 |
2,35 |
|||
|
300 |
0,87 |
1,86 |
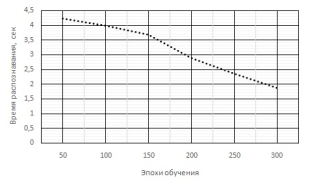
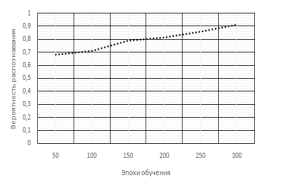
Рис. 8. Результаты работы ИНС R-CNN, обученной методом обратного распространения ошибки
Для оценки эффективности применения ИНС в задачах дешифрирования выполнено сравнение результатов дешифрирования ИНС R-CNN, обученной методом обратного распространения ошибки и оператором-дешифровщиком. Результаты сравнительного анализа представлены в таблице 2.
Таблица 2
Результаты ИНС R - CNN , обученной методом обратного распространения ошибки и оператора-дешифровщика
|
Способ дешифрирования |
Вероятность распознавания |
Время распознавания , мин |
|
ИНС R-CNN, обученная методом обратного распространения ошибки |
0,88 |
3 мин |
|
Оператор-дешифровщик |
0,9 |
15 мин |
В настоящей статье представлен:
- Анализ метода обучения ИНС обратного распространения ошибки, который ускоряет процесс дешифрирования объектов ДЗЗ, сохраняя при этом высокую вероятность распознавания объекта на аэроснимке, что увеличивает эффективность решении задачи дешифрирования в боевой обстановке, а также при проведении летных испытаний.
- Показан пример автоматического обнаружения объекта ДЗЗ с помощью алгоритма ИНС R-CNN, обученной методом обратного распространения ошибки.
- Анализ сравнения решении задачи дешифрирования ИНС R-CNN, обученной методом обратного распространения ошибки и оператором дешифровщиком показывает, что для решения задачи дешифрирования ИНС занимает меньшее время с высокой точностью распознавания.
Литература:
- Гафаров Ф. М., Галимянов А. Ф. Искусственные нейронные сети и приложения: учеб. Пособие. Казань: Изд-во Казан. ун-та, 2018. 121 с.
- Молчанов А. С., Чаусов Е. В. Теория и практика распознавания инженерных сооружений, промышленных предприятий и объектов железнодорожного транспорта при дешифрировании аэрофотоснимков. М.: Перо, 2024. 248 с.
- Дэвис Р., Терк М. Компьютерное зрение. Современные методы и перспективы развития. М.: ДМК Пресс, 2022. 690 с.
- Л. Б. Соколинский Лекции по курсу «Глубокие нейронные сети» 3–19 с.
- Чаусов Е. В., Молчанов А. С. Математическое и программное обеспечение обработки цифровых изображений при оценивании линейного разрешения аэрофотографических систем // Кибернетика и программирование. 2020. № 1. С. 42–52.







