В работе рассматривается ограниченная самосопряженная обобщенная модель Фридрихса. Показывается, что замыкание численного диапазона этой модели состоит из отрезка и исследован его структура.
Ключевые слова:численный диапазон, существенный и дискретный спектры, обобщенная модель Фридрихса, первый комплимент Шуура.
Пусть ![]() комплексное гильбертово пространство и
комплексное гильбертово пространство и ![]() линейный оператор с областью определения
линейный оператор с областью определения ![]() . Множество
. Множество
![]()
называется численным диапазоном оператора ![]() . Из определения видно, что множество
. Из определения видно, что множество ![]() является подмножеством комплексной плоскости и геометрические свойства множества
является подмножеством комплексной плоскости и геометрические свойства множества ![]() дает некоторые информации об операторе
дает некоторые информации об операторе ![]() .
.
Изучение численного диапазона линейного оператора в гильбертовом пространстве является одним из основных методов в изучении местоположения спектра таких операторов. Это понятие впервые введено в работе [1] и доказано, что численный диапазон матрицы содержит все ее собственные значения. В работе [2] показано, что численный диапазон оператора является выпуклым. Отметим, что выше сказанные результаты верны не только для матриц, но и в более общем случае для любого линейного ограниченного оператора. В работе [3] доказано, что спектр любого линейного ограниченного оператора содержится в замыкании численного диапазона этого оператора. Вслед за этим это понятие обобщено разными способами, см. например [4,5,6].
В работе [7] изучаются основные свойства численного диапазона линейного оператора и вычислен численный диапазон обобщенной модели Фридрихса в частном случае. Кроме того, там приведены примеры на вычисление численного диапазона операторов разного характера.
В настоящей работе установлена структура численного диапазона обобщенной модели Фридрихса и обсуждаются всевозможные случаи. Отметим, что такие модели обычно встречаются в задачах квантовой механики, статистической механики и гидродинамики.
Обозначим через ![]()
![]()
![]() и
и ![]() — множество натуральных, целых, вещественных и комплексных чисел, соответственно.
— множество натуральных, целых, вещественных и комплексных чисел, соответственно.
Теперь перейдем к постановку задачи и формулировки основных результатов настоящей работы.
Пусть ![]() - трехмерный тор, т. е. куб
- трехмерный тор, т. е. куб ![]() — с соответствующим отождествлением противоположных граней. Всюду в работе
— с соответствующим отождествлением противоположных граней. Всюду в работе ![]() рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в
рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в ![]() по модулю
по модулю ![]() .
.
Пусть ![]() — гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на
— гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на ![]() . Обозначим через
. Обозначим через ![]() прямую сумму пространств
прямую сумму пространств ![]() и
и ![]() , т. е.
, т. е. ![]() .
.
Рассмотрим обобщенный модель Фридрихса ![]() действующего в гильбертовом пространстве
действующего в гильбертовом пространстве ![]() как
как ![]() блочно-операторная матрица
блочно-операторная матрица
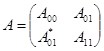 ,
,
где элементы ![]() , определяются по формулам
, определяются по формулам
![]()
![]() ,
, ![]()
Здесь ![]() ,
, ![]() ,
, ![]()
![]() и
и ![]()
![]() вещественнозначные непрерывные функции на
вещественнозначные непрерывные функции на ![]() , а
, а ![]() сопряженный оператор к
сопряженный оператор к ![]() .
.
Легко проверить, что при этих предположениях матричный оператор ![]() , является ограниченным и самосопряженным в гильбертовом пространстве
, является ограниченным и самосопряженным в гильбертовом пространстве ![]() .
.
Пусть оператор ![]() действует в
действует в ![]() как
как
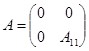 .
.
Оператор возмущения ![]() -
-![]() оператора
оператора ![]() является самосопряженным оператором ранга 2. Следовательно, из известной теоремы Г. Вейля о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора
является самосопряженным оператором ранга 2. Следовательно, из известной теоремы Г. Вейля о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора ![]() совпадает с существенным спектром оператора
совпадает с существенным спектром оператора ![]() . Известно, что
. Известно, что
![]() ,
,
где числа ![]() и
и ![]() определяются следующим образом:
определяются следующим образом:
![]() ,
, ![]() .
.
Из последних фактов следует, что ![]() .
.
Чтобы определит дискретный спектр оператора ![]() наряду с этим оператором рассмотрим ещё оператор
наряду с этим оператором рассмотрим ещё оператор ![]() который формально определяется следующим образом:
который формально определяется следующим образом:
![]()
![]()
Так определенный оператор обычно называется первый комплимент Шуура.
Легко проверяется, что оператор ![]() имеет собственное значение
имеет собственное значение ![]() тогда и только тогда, когда оператор
тогда и только тогда, когда оператор ![]() имеет нулевое собственное значение. Следовательно,
имеет нулевое собственное значение. Следовательно,
![]()
где
![]() .
.
Надо отметить, что дискретный спектр оператора ![]() играет важную роль при исследовании его численного диапазона.
играет важную роль при исследовании его численного диапазона.
Далее, будем предполагать, что функция ![]() имеет непрерывные частные производные второго порядка, невырожденный минимум в точках
имеет непрерывные частные производные второго порядка, невырожденный минимум в точках ![]()
![]() и невырожденный максимум в точках
и невырожденный максимум в точках ![]()
![]() .
.
Тогда из непрерывности функции ![]() на
на ![]() следует, что
следует, что
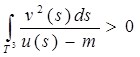 ,
, ![]() ,
,
являются конечными интегралами.
В качестве такой функции ![]() можно взят
можно взят
![]() ,
, ![]() ,
, ![]()
Обозначим через ![]() и
и ![]() число точек
число точек ![]()
и ![]() , соответственно для которых
, соответственно для которых
![]()
![]()
причем ![]() при
при ![]() , здесь
, здесь
![]()
![]()
![]()
Очевидно, что функция ![]() имеет невырожденный минимум в точках
имеет невырожденный минимум в точках ![]() , невырожденный максимум в точках
, невырожденный максимум в точках ![]() и
и ![]()
![]() . Таким образом, множество значений функций
. Таким образом, множество значений функций ![]() совпадает с отрезком [0, 6].
совпадает с отрезком [0, 6].
Следуя схемы работы [8] показывается, что оператор ![]() имеет не более чем двух простых собственных значений, один из них лежит левее точки
имеет не более чем двух простых собственных значений, один из них лежит левее точки ![]() , а второе правее точки
, а второе правее точки ![]() . В случае существовании обозначим их через
. В случае существовании обозначим их через ![]() и
и ![]() соответственно.
соответственно.
Положим
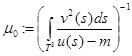 ,
, 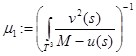 .
.
Следующие теоремы описывают структуру численного диапазона оператора ![]() .
.
Теорема 1. Пусть ![]() .
.
1) Если ![]() , то верно равенство
, то верно равенство ![]()
2) При ![]() имеет место равенство
имеет место равенство ![]() .
.
Теорема 2. Пусть ![]()
1) Если ![]() то
то ![]() ;
;
2) Если ![]() и
и ![]() , то
, то ![]() ;
;
3) Если ![]() и
и ![]() , то
, то ![]()
4) Если ![]() то
то ![]()
Замечание 1. Если ![]() , т. е.
, т. е.
![]()
при ![]() , имеем случай утверждении 1), а при
, имеем случай утверждении 1), а при ![]() , случай утверждении 4) теоремы 2.
, случай утверждении 4) теоремы 2.
Замечание 2. Условие 2) и 3) теоремы 2 соответствуют в случае
![]() .
.
Теорема 3. Пусть ![]() .
.
1) Если ![]() , то имеет место равенство
, то имеет место равенство ![]() ;
;
2) При ![]() верно равенство
верно равенство ![]() .
.
При доказательстве теоремы 1–3 ключевой роль играет нахождение условия существования собственных значений оператора ![]() и выпуклость численного диапазона.
и выпуклость численного диапазона.
Литература:
1. O. Toeplitz. Das algebraische Analogon zu einem Satze von Fejer. Math. Z., 2:1–2 (1918), 187–197.
2. F. Hausdorff. Der Wertvorrat einer Bilinearform. Math. Z., 3:1 (1919), 314–316.
3. A. Wintner. Zur Theorie der beschrankten Bilinearformen. Math. Z., 30:1 (1929), 228–281.
4. H. Langer, A. S. Markus, V. I. Matsaev, C. Tretter. A new concept for block operator matrices: the quadratic numerical range. Linear Algebra Appl., 330:1–3 (2001), 89–112.
5. L. Rodman, I. M. Spitkovsky. Ratio numerical ranges of operators. Integr. Equ. Oper. Theory, 71 (2011), 245–257.
6. M. T. Heydari. Numerical range and compact convex sets. Rend. Circ. Mat. Palermo, 60 (2011), 139–143.
7. Т. Х. Расулов, Г. И. Ботиров. Численный диапазон обобщенной модели Фридрихса. Узб. Матем. Журнал, № 2 (2013), стр. 3–10.
8. Т. Х. Расулов. О структуре существенного спектра модельного оператора нескольких частиц. Математические заметки. 83:1 (2008), 78–86.







