В статье описана методика работы с результатами испытаний деталей. С помощью методов машинного обучения удалось научиться предсказывать максимальное значение силы на растяжение, которую выдерживает деталь перед полным разрушением. Лучшую модель из исследуемых удалось выбрать с помощью инструментов системного инжиниринга. Предлагаемая методика работы с экспериментальными данными в дальнейшем может являться основой для моделей надёжности авиационных систем.
Ключевые слова: метод анализа иерархий, метод Гермейера, обработка данных, моделирование, машинное обучение, метрики, прочностные испытания, надёжность авиационных систем.
Введение
Использование компьютерного моделирования в авиастроении помогает добиться повышения качества изделий, снизить стоимость и сроки проектирования. Системный подход к безбумажному проектированию предполагает, что проектные решения проверяются моделированием на каждом этапе разработки [1]. Для сокращения стоимости и сроков проектирования нужно выбирать самые оптимальные решения ещё на ранних этапах. Компьютерное моделирование может облегчить поиск таких решений.
Системный инжиниринг — это междисциплинарный подход к разработке сложных технических систем, который позволяет учитывать взаимосвязи и рассматривать систему как единое целое. Инструменты системного инжиниринга позволяют проводить сравнение показателей, сложно сравнимых между собой напрямую, выбирать самые оптимальные решения по совокупности факторов. Одними из удобных инструментов системного инжиниринга являются метод анализа иерархий (МАИ) и метод Гермейера. Они позволяют проводить многокритериальную оценку альтернатив с учётом значимости каждого сравниваемого критерия.
При проектировании авиационной техники критически важно обеспечить заданные показатели надёжности систем. Это можно сделать за счёт повышения коэффициентов запаса и введения избыточности. Моделирование показателей надёжности сложных технических систем является нетривиальной задачей по причине большого количества разнородных факторов, которые необходимо учитывать. Для разработки моделей надёжности систем на основе экспериментальных данных об испытаниях отдельных компонентов предлагается использовать машинное обучение.
Постановка задачи
В данной работе предлагаемый подход опробован на примере записей, полученных при экспериментальном разрушении деталей на испытательной машине. С помощью методов машинного обучения можно предсказать максимальное значение силы на растяжение, которую выдерживает деталь перед полным разрушением. С точки зрения машинного обучения рассматриваемая задача является задачей регрессии — необходимо рассчитать значение одной непрерывной количественной переменной (максимальной силы) по известным характеристикам геометрии детали. С помощью методов системного инжиниринга необходимо выбрать оптимальный вариант обучения.
Таблица 1
Требования, функции, элементы решения
|
Требования |
Функции |
Элементы решения |
|
Получить экспериментальные данные |
Проведение эксперимента по разрушению детали с записью параметров |
Универсальная испытательная машина «TIME WDW-300E» |
|
Определить прочностные характеристики детали по её геометрическим параметрам |
Определение прочности на разрыв решением задачи регрессии |
DecisionTreeRegressor |
|
RandomForestRegressor |
||
|
LinearRegression |
||
|
CatBoostRegressor |
||
|
SVR |
||
|
KNeighborsRegressor |
||
|
Определить наиболее оптимальную модель машинного обучения |
Сравнение доступных альтернатив по метрикам, полученным в результате обучения моделей, выбор лучшей модели для дообучения и дальнейшего использования |
Метод анализа иерархий — поиск весов важности каждой метрики |
|
Метод Гермейера — сравнение моделей с учетом весов важности метрик |
Работа с данными
Рассматриваемые детали представляют собой пластины из алюминиево-магниевого сплава толщиной 1.9 мм с различными конфигурациями отверстий. Всего для эксперимента выбрано 40 деталей. Экспериментальное разрушение деталей выполнено на универсальной испытательной машине «TIME WDW-300E». В ходе испытаний программно установлена скорость нагружения 5 мм/мин. Основные характеристики испытательной машины:
— наибольшая предельная нагрузка: 300 кН;
— пределы погрешности силоизмерителя: ±1 %;
— диапазон скоростей нагружения: от 0.005 до 500 мм/мин;
— масса: не более 2000 кг.
Этапы работы с экспериментальными данными представлены на рис. 1. Сбор данных, выбор признаков для модели машинного обучения и выбор самой модели относятся к исследовательским этапам. После этих этапов необходимо совершенствование модели машинного обучения таким образом, чтобы достичь заданного качества предсказания. Это может происходить в несколько итераций.
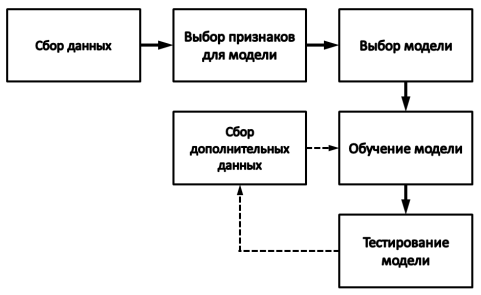
Рис. 1. Этапы работы с экспериментальными данными
Для работы с экспериментальными данными создана консольная программа «Structural Failure Predictor» на языке Python 3. Программа осуществляет подготовку экспериментальных данных для работы с моделями машинного обучения, поиск лучшей модели и тестирование обученной модели. Программа загружает свои настройки из конфигурационного файла. Далее программа выполняет чтение единого файла с описанием всех испытаний и отдельных файлов для каждого испытания. Имеющиеся данные программа преобразует с учётом смещений нулей при измерении силы нагружения и деформации детали, рассчитывает дополнительные признаки. Программа выводит в отдельных окнах графики, позволяющие оценить подготовленные для обучения данные. Далее программа осуществляет поиск лучшей модели с помощью инструмента автоматизированного подбора гиперпараметров, а затем — тестирование лучшей модели с выводом результатов в консоль.
Сбор данных выполнен с помощью программы «WinWDW», которая позволяет полностью управлять процессом испытания детали. С момента начала нагружения до полного разрушения детали записываются следующие параметры с частотой 17 Гц:
— сила нагружения, кН;
— деформация детали по экстензометру, мм;
— перемещение траверсы машины, мм;
— время с момента начала нагружения, сек.
Записи разрушения деталей в координатах «сила растяжения — деформация», преобразованные программой «Structural Failure Predictor» с учётом смещений нулей, представлены на рис. 2.
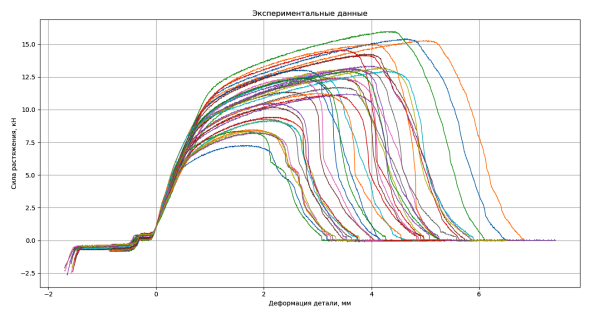
Рис. 2. Записи разрушения деталей
Экспериментальная зависимость максимальной силы нагружения детали от геометрии представлена на рис. 3. Диаграмма рассеяния показывает: чем меньше количество отверстий и диаметр каждого отверстия, тем больше максимальная сила нагружения.
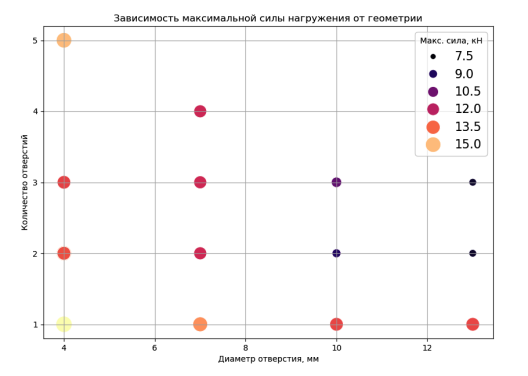
Рис. 3. Зависимость максимальной силы от геометрии детали
Для выбора подходящих для модели машинного обучения признаков можно воспользоваться матрицей корреляции. Матрица корреляции показывает взаимосвязи входных признаков между собой и с целевым признаком. Одним из перспективных алгоритмов расчёта коэффициентов корреляции является алгоритм «Phi_K» [2]. Матрица корреляции «Phi_K», сгенерированная программой «Structural Failure Predictor», представлена на рис. 4. При рассмотрении матрицы корреляции видно, что геометрические характеристики детали значительно влияют на максимальную силу нагружения.
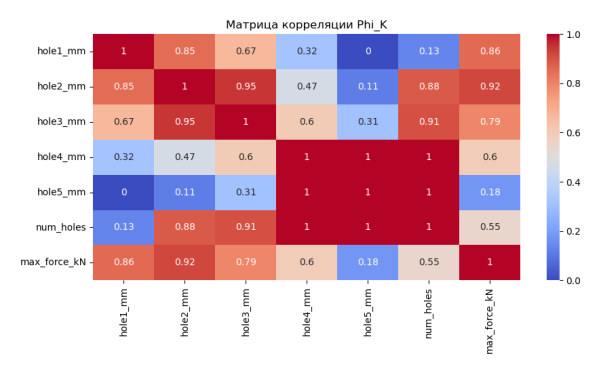
Рис. 4. Матрица корреляции «Phi_K»
Программа «Structural Failure Predictor» делит имеющиеся данные на обучающую и тестовую выборку в заданном соотношении (3:1) и выполняет поиск лучшей модели, используя только обучающую выборку. При поиске лучшей модели программа записывает метрики оценки каждой модели — табл. 2. В таблице средние значения и среднеквадратичные отклонения (СКО) метрик оценки посчитаны по результатам кросс-валидации каждой модели. Средние и медианные абсолютные ошибки показывают отклонения предсказанных значений целевого признака от истинных значений. Коэффициент детерминации — это доля дисперсии целевого признака, объясняемая рассматриваемой моделью. Чем ближе коэффициент детерминации к единице, тем выше обобщающая способность модели.
Таблица 2
Метрики оценки моделей
|
Метрика |
DecisionTreeRegressor |
RandomForestRegressor |
LinearRegression |
CatBoostRegressor |
SVR |
KNeighborsRegressor |
|
Средняя Mean Absolute Error, кН |
0.598200 |
0.637564 |
0.649408 |
0.660813 |
0.918622 |
0.995760 |
|
СКО Mean Absolute Error, кН |
0.205083 |
0.190433 |
0.196580 |
0.258555 |
0.468568 |
0.404001 |
|
Средняя Median Absolute Error, кН |
0.438000 |
0.496029 |
0.454041 |
0.485839 |
0.809661 |
0.878400 |
|
СКО Median Absolute Error, кН |
0.270067 |
0.171381 |
0.115725 |
0.317259 |
0.502971 |
0.516789 |
|
Средний коэффициент детерминации |
0.734071 |
0.739488 |
0.605382 |
0.609362 |
0.371265 |
0.477092 |
|
СКО коэффициента детерминации |
0.270970 |
0.241681 |
0.512143 |
0.483150 |
0.914493 |
0.496137 |
|
Среднее время обучения, сек |
0.007353 |
0.188927 |
0.020060 |
0.968233 |
0.007634 |
0.009658 |
|
СКО времени обучения, сек |
0.001041 |
0.008437 |
0.001907 |
0.094215 |
0.000698 |
0.000691 |
|
Среднее время предсказания, сек |
0.006109 |
0.012034 |
0.005888 |
0.005760 |
0.004795 |
0.006268 |
|
СКО времени предсказания, сек |
0.000477 |
0.000867 |
0.000472 |
0.000954 |
0.000405 |
0.000918 |
Оценка и сравнение альтернатив
Программа «Structural Failure Predictor» при работе алгоритма поиска лучшей модели рассчитала и вывела 10 метрик оценки. Большое количество разных метрик трудно для прямого человеческого восприятия. Далее проведена численная оценка важности каждой метрики с помощью метода анализа иерархий. Метод предполагает попарное сравнение важности всех метрик с помощью оценок по шкале от «подавляюще превосходит» до «подавляюще уступает». Результаты попарного сравнения записываются в матрицу, затем рассчитывают итоговый вес каждой метрики оценки — табл. 3. Чем больше значение веса метрики, тем более значимый вклад она вносит в выбор лучшей модели.
Таблица 3
Расчёт важности метрик оценки по МАИ
|
Метрики оценки |
Вес |
|
Средняя Mean Absolute Error, кН |
0.245 |
|
СКО Mean Absolute Error, кН |
0.040 |
|
Средняя Median Absolute Error, кН |
0.200 |
|
СКО Median Absolute Error, кН |
0.044 |
|
Средний коэффициент детерминации |
0.210 |
|
СКО коэффициента детерминации |
0.035 |
|
Среднее время обучения, сек |
0.090 |
|
СКО времени обучения, сек |
0.017 |
|
Среднее время предсказания, сек |
0.100 |
|
СКО времени предсказания, сек |
0.018 |
Далее проведена оценка моделей по методу Гермейера. Для использования этого метода необходимо преобразовать значения метрик оценки таким образом, чтобы более высокое значение соответствовало лучшему качеству модели. В исходном виде это справедливо лишь для среднего коэффициента детерминации, поэтому остальные метрики преобразованы по следующему закону (1):
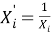
где
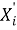
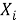
Формула для оценки оптимальности каждой альтернативы по методу Гермейера (в долях от лучшего значения метрики) имеет вид (2):
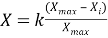
где
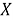
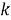
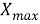
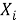
Результаты расчёта оптимальности альтернатив по методу Гермейера для каждой модели машинного обучения представлены в табл. 4.
Таблица 4
Оценки оптимальности альтернатив по методу Гермейера
|
Метрика |
DecisionTreeRegressor |
RandomForestRegressor |
LinearRegression |
CatBoostRegressor |
SVR |
KNeighborsRegressor |
|
Средняя Mean Absolute Error, кН |
0.000 |
0.015 |
0.019 |
0.023 |
0.086 |
0.098 |
|
СКО Mean Absolute Error, кН |
0.003 |
0.000 |
0.001 |
0.011 |
0.024 |
0.021 |
|
Средняя Median Absolute Error, кН |
0.000 |
0.023 |
0.007 |
0.020 |
0.092 |
0.100 |
|
СКО Median Absolute Error, кН |
0.025 |
0.014 |
0.000 |
0.028 |
0.034 |
0.034 |
|
Средний коэффициент детерминации |
0.002 |
0.000 |
0.038 |
0.037 |
0.104 |
0.074 |
|
СКО коэффициента детерминации |
0.004 |
0.000 |
0.018 |
0.017 |
0.026 |
0.018 |
|
Среднее время обучения, сек |
0.000 |
0.087 |
0.057 |
0.090 |
0.003 |
0.022 |
|
СКО времени обучения, сек |
0.006 |
0.016 |
0.011 |
0.017 |
0.000 |
0.000 |
|
Среднее время предсказания, сек |
0.022 |
0.060 |
0.019 |
0.017 |
0.000 |
0.024 |
|
СКО времени предсказания, сек |
0.003 |
0.010 |
0.003 |
0.011 |
0.000 |
0.010 |
|
Интегральный критерий Гермейера |
0.064 |
0.225 |
0.173 |
0.270 |
0.369 |
0.401 |
Интерпретировать оценки оптимальности альтернатив по методу Гермейера можно следующим образом: чем меньше значение оценки, тем лучше альтернатива. Если значение оценки какой-то метрики равно нулю, то альтернатива является лидером по этой метрике. Интегральный критерий Гермейера можно вычислить как сумму оценок оптимальности метрик альтернативы.
Наименьшее значение интегрального критерия Гермейера показывает лучшую модель — это DecisionTreeRegressor [4]. Оценки метрик позволяют определить, что у этой модели средние и медианные ошибки предсказаний являются минимальными среди всех моделей. Также минимально среднее время обучения. При этом среднеквадратичные отклонения небольшие. Высокое значение коэффициента детерминации при кросс-валидации говорит о хорошей обобщающей способности модели.
Другой хорошей моделью является LinearRegression [4]. Значения оценок этой модели немного хуже по метрикам средних ошибок и по коэффициенту детерминации, однако у этой модели низкие среднеквадратичные отклонения ошибок.
Тестирование лучшей модели выполнено на тех данных, которые не были задействованы при обучении. При тестировании средняя абсолютная ошибка (Mean Absolute Error) максимального значения силы составила 0.711 кН. Сравнение полученного значения средней абсолютной ошибки с исходными данными (рис. 2) показывает, что результат удовлетворительный. Другой важной метрикой, рассчитанной при тестировании модели, является коэффициент детерминации. Значение коэффициента детерминации — 0.7925, следовательно, в 79.25 % случаев предсказание модели ближе к истине, чем простое среднее значение целевого признака.
Заключение
Таким образом, предлагаемый в работе подход опробован экспериментально. С помощью методов машинного обучения удалось научиться предсказывать максимальное значение силы на растяжение, которую выдерживает деталь перед полным разрушением. Лучшую модель из исследуемых удалось выбрать с помощью инструментов системного инжиниринга. Опробована методика работы с экспериментальными данными, которая в дальнейшем может являться основой для более сложных моделей надёжности авиационных систем.
Литература:
- Суздалева, Е. А. САПР в авиастроении и проблемы, возникающие при переходе на безбумажное проектирование / Е. А. Суздалева, А. О. Марченков // Вестник науки и образования. — 2019. — № 21 (75).
- Документация к библиотеке «Phi_K» [Электронный ресурс]. — 2024. — Режим доступа: https://phik.readthedocs.io/en/latest/, свободный (дата обращения 13.10.2024).
- А. А. Бородкин Системный инжиниринг для поиска технических решений. Сборник лекций, 6-е изд. / А. А. Бородкин, Г. А. Ефименко. — М.: МФТИ, 2019. — 142 с.
- Документация к библиотеке «Scikit-learn» [Электронный ресурс]. — 2024. — Режим доступа: https://scikit-learn.org/stable/, свободный (дата обращения 13.10.2024).
- Бринк Х. Машинное обучение / Х. Бринк, Д. Ричардс, М. Феверолф. — СПб.: Питер, 2017. — 336 с.







