В данной статье представлен аналитический обзор факторов, влияющих на эффективность эксплуатации грузового транспорта. Из всех приведенных факторов был выделен один из главных факторов — расстояние перевозки. Для оптимизации данного фактора был выбран метод муравьиной колонии, отличающийся простотой вычислений, и точностью конечного результата. На основе данного алгоритма была создана программа, рассчитывающая минимальное расстояние между пунктами. Данная программа была реализована при помощи программы Microsoft Excel.
Ключевые слова: оптимизация, муравьиный алгоритм, расстояние перевозки, платформа Microsoft Excel, эффективность эксплуатации транспорта.
Введение
С началом развития информационных технологий человечество вступило в новую эру развития. И в транспортной отрасли также появляется различное программное обеспечение, позволяющие более эффективно использовать ресурсы, и тем самым упрощать работу, или уменьшать издержки.
Цель данной статьи — создание программы, позволяющей повысить эффективность использования транспорта.
Задачами данной статьи является анализ факторов, влияющих на эффективность использования транспорта, выделение одного из значимых из них, и создание программы, позволяющей оптимизировать данный фактор.
Аналитическая часть
Каждая транспортная компания проводит мероприятия по повышению эффективности использования транспорта что непосредственно влияет на эффективность работы транспортной компании и повышает ее конкурентоспособность. Также на эффективность эксплуатации транспорта влияют и внешние факторы. К таким факторам относятся качество дорожного покрытия, расстояние транспортировки, транспортная инфраструктура, расположенная в городах, и на магистралях, климат, в котором используется транспорт. Также на эффективность эксплуатации транспорта влияют такие показатели как техническое состояние, которое напрямую связано с количеством выездов его на линию, качество проводимого ремонта, уровень профессионализма водителей, который напрямую зависит на уровень технического состояния в процессе эксплуатации. Так по данным аналитического портала «bip.ru» с увеличением водительского стажа уровень безаварийности увеличивается в разы [1] (Рисунок 1).
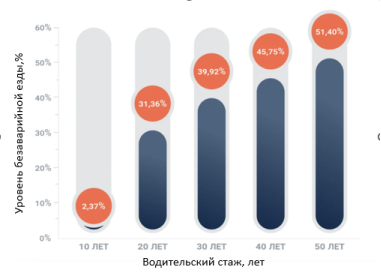
Рис. 1. Доля безаварийности в зависимости от стажа
Все вышеизложенные факторы можно отслеживать с помощью программных обеспечений, и датчиков, которые устанавливаются на узлы и агрегаты автомобилей. Такие программы, например, встраиваются в бортовую систему автомобиля, или работают дистанционно. Они позволяют отслеживать различные технические параметры автомобиля. И предупреждать водителя или другого человека следящего за состоянием транспорта о возможной неисправности.
Одним из немаловажных факторов при перевозках грузов автомобильным транспортом является расстояние перевозки. Данный фактор влияет на уровень расходов, связанных с эксплуатацией транспорта, и время нахождения автомобиля в наряде. Существуют различные методы по расчету оптимального расстояния такие как транспортная задача, метод ветвей и границ, метод Дейкстры, метод полного перебора, но все они имеют как свои преимущества, так и свои недостатки. Например, преимуществом метода полного перебора является то, что он является самым точным из всех вышеизложенных, но его самым большим недостатком является время, затрачиваемое на расчеты. Так при расчете пути при 60 пунктах время на расчет составит 54481,31 сек. или 15 ч. что достаточно долго. Существует также алгоритм муравьиной колонии, который позволяет решать задачи оптимизации пути при большом количестве пунктов. Муравьиные алгоритмы основаны на имитации природных механизмов самоорганизации муравьев [2]. Рассчитать путь используя метод муравьиного алгоритма можно при помощи следующих формул:
Желание посетить точку определяется по формуле:
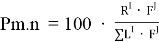
где: R- привлекательность пути в зависимости от расстояния
F — количество феромона отложенного 1 точки до последующей
I — параметр, контролирующий влияние на выбор пути расстояния, I=1
J — параметр, контролирующий влияние на выбор пути количества феромона, принимается J =1
Привлекательность пути в зависимости от расстояния определяется по формуле:
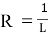
где: L– расстояние от 1 точки до последующей.
После первой итерации необходимо обновить «феромон». Это делается для того, чтобы в последующих расчетах учитывался проход каждого муравья в следствии этого находился оптимальный путь. Обновление феромона вычисляется по формуле:
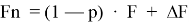
где: p– период выветривания феромона, если p = 0 то феромон не выветривается и учитываются все пройденные маршруты что повышает риск неоптимального решения. Если p> 0, то феромон выветривается в соответствии с заданным числом.
∆F — количество феромона отложенного первым муравьем.
Количество феромона отложенного первым муравьем определяется по формуле:
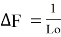
где: L о – длина маршрута первого муравья.
Платформой для создания программы была выбрана программа Microsoft Excel. Выбор данной программы связан с тем, что данная программа является часто используемой офисной программой и отличается простотой и интуитивно понятной работой в ней. В последующем для работы созданной программы не будет необходимости скачивать отдельную программу, необходимо будет лишь скачать табличный документ с программой. Также не маловажным плюсом будет возможность любого человека, использущего данную программу изменять ее на свое усмотрение.
Для расчета кратчайшего пути в Microsoft Excel используются встроенные функции, и макрос, позволяющий создать цикл повторений расчетов для необходимого количества итераций. Макрос написан посредством встроенного редактора «Microsoft Visual Basic Application». Фрагмент данного макроса представлен на рисунке 2.
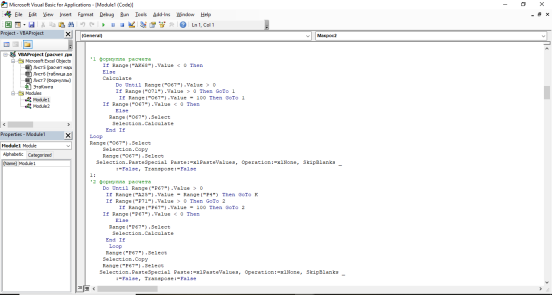
Рис. 2. Макрос для расчета алгоритма
Для удобства использования программы на отдельном листе под названием «Таблица данных» заполняется реестр адресов в таблицу с их географическими координатами (рисунок 3). Данные адреса сохраняться как база данных, и при необходимости можно будет выбрать для расчета любой из этих адресов. Координаты адресов можно найти при помощи поисковых сервисов, или карт. Географические координаты не записываются в таблицу напрямую из интернета для возможности работы программы без подключения к сети Интернет.
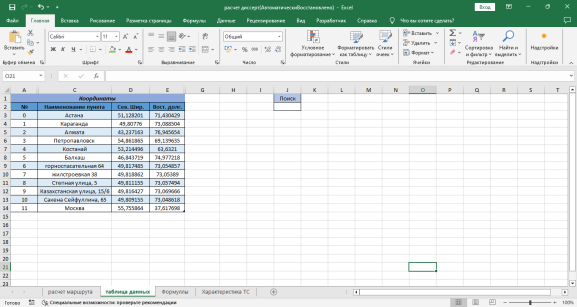
Рис. 3. Таблица для записи адресов
Именно исходя из географических координат точек программа рассчитывает расстояние между точками по формуле гаверсинуса [3].
Формула гаверсинуса имеет следующий вид:
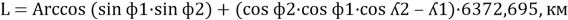
Где: Ф — широта первой и второй точек в радианах;
ʎ — долгота первой и второй точек в радианах.
Данная формула позволяет точно вычислить расстояние между двумя точками на земном шаре.
Расчет кратчайшего расстояния между пунктами производится на вкладе «Расчет маршрута». Вид вкладки расчёта маршрута представлен на рисунке 4. На главном листе представлена таблица с выпадающим списком пунктов, которые необходимо посетить. Данные для этого списка добавляются из таблицы во вкладке «Таблица данных». Затем при помощи формулы записываются их географические координаты. Для того чтобы провести вычисления необходимо нажать кнопку «Рассчитать» которая запустит макрос.
После проведения всех вычислений и нахождения кратчайшего пути данные в порядке посещения пунктов запишутся в таблицу. Также на карте маркерами будут отмечены пункты посещения.
В отдельной таблице указываются данные маршрута, его километража, расход топлива, и время, которое будет потрачено на проезд по маршруту.
Для отчистки всех полей для нового расчета используется кнопка «Очистить», тогда при ее нажатии все данные будут полностью очищены.
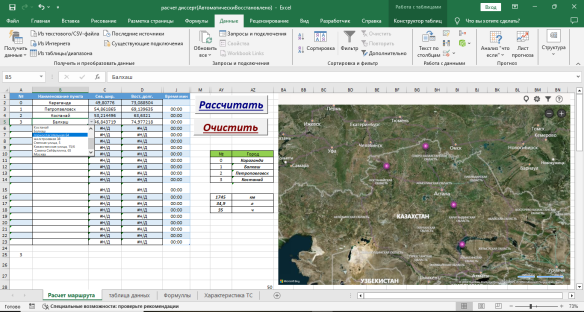
Рис. 4. Вкладка «Расчёт маршрута»
Выводы
Был проведен анализ факторов, влияющих на эффективность эксплуатации транспорта. Был выделен фактор расстояния между пунктами посещения который напрямую влияет на эффективность транспортировки. Был проведен анализ методов, позволяющих рассчитать оптимально расстояние. Из всех перечисленных методов был выбран метод муравьиной колонии, отличающийся простотой вычислений, и достаточной точностью. На основе данного алгоритма была создана программ, на платформе Microsoft Excel. Данная программа может быть использована в учебных целях для студентов специальностей, связанных с транспортом.
Литература:
- Аналитический портал «bip.ru» — URL: https://bip.ru/ (дата обращения: 10.11.2024).
- С. Д. Штовба Муравьиные алгоритмы журнал Мастерская Решений — URL: https://docviewer.yandex.kz/view/0/?(дата обращения: 9.11.2024).
- Материал из Википедии — свободной энциклопедии — URL: https://en.wikipedia.org/wiki/Haversine_formula (дата обращения: 10.11.2024).







