В статье автор пытается рассмотреть вопрос по решению задач, чтобы обучение доставляло учащимся удовольствие, способствовало их активности и самостоятельности.
Ключевые слова: задача, конструкция, исследование, квадратный корень, смешанное число.
В настоящее время трудно переоценить важность решения задач как одного из основных видов учебной деятельности по математике, который не только способствует усвоению учебного материала, но и играет ключевую роль в развитии умений и навыков, необходимых для успешного обучения. Решение задач позволяет школьникам применять теоретические знания на практике, что значительно углубляет их понимание предмета. Эффективность учебной работы в значительной степени зависит от того, какие задачи предлагаются учащимся, в какой последовательности они вводятся и какими методами решаются. Например, важно учитывать уровень сложности задач: начинать с простых, постепенно переходя к более сложным, чтобы не вызвать у детей чувство неуверенности. Это позволяет создать прочный фундамент знаний, на котором можно строить дальнейшее обучение. Кроме того, активное участие учеников в процессе решения задач является критически важным. Когда учащиеся самостоятельно ищут решения, обсуждают их с одноклассниками и учителем, они не только развивают критическое мышление, но и учатся работать в команде. Такие навыки будут полезны не только в учебе, но и в будущей профессиональной деятельности. Важно также отметить, что решение задач способствует формированию у школьников исследовательского подхода. Они учатся не просто находить правильные ответы, но и задавать вопросы, анализировать условия задачи и рассматривать различные способы её решения. Это развивает у них креативность и способность находить нестандартные решения, что является важным качеством в современном мире.
Как сделать так, чтобы решение задач приносило ученикам радость и удовольствие, чтобы класс превращался в творческую студию, где из изучаемого материала на глазах у всех появляются математические абстракции? Как выдвигаемые предположения могли бы будоражить детское любопытство, а смелость озвучиваемых гипотез восхищала? Как добиться того, чтобы доказательства воспринимались как естественное стремление к поиску истин? Создание атмосферы, в которой ученики будут чувствовать себя вовлеченными и заинтересованными, является ключевым моментом. Необходимо, чтобы каждый новый шаг в решении задач не вызывал у детей страх, а наоборот, становился возможностью проявить творчество и интуицию.
Организация и координация работы класса по решению задач представляет собой большое мастерство. Это требует сочетания глубоких знаний математики с эффективными методическими подходами, а также устойчивых педагогических принципов и обширного коммуникативного опыта. В этом контексте могут быть особенно полезны идеи, оставшиеся актуальными с учений французского педагога-математика начала прошлого века Лэзана, который подчеркивал важность «сохранять видимость игры, уважать свободу ребенка, поддерживая иллюзию его собственного открытия истины» [2].
В настоящее время играют большую роль рекомендации знаменитого американского педагога-математика Д. Пойа, который подчеркивал, что учащийся «должен приобрести как можно больше опыта самостоятельной работы. Но если он оставлен наедине с задачей без всякой помощи или если эта помощь недостаточна, — это может не принести ему никакой пользы. …Поэтому помощь учителя должна быть осторожной и неназойливой» [3]. Полезными могут быть также советы многих выдающихся российских математиков и педагогов, включая новаторов и рядовых школьных учителей математики, которые на каждом занятии обеспечивают решение задач на различных этапах усвоения материала.
Однако самым важным являются сами задачи, точнее их конструкции (системы, циклы, блоки, цепочки, серии и т. д.), разработанные педагогом или методистом для урока. Они способны по-настоящему увлечь учеников решением и вести их по ступеням познания к открытию математических истин, а порой и к созданию небольших теорий. Эти задачи должны формировать атмосферу активной исследовательской деятельности, а роль учителя заключается в том, чтобы поддерживать высокий уровень энтузиазма, вдохновлять процесс познания, наполнять его человеческими ценностями, направлять идеи и устремления детей в правильное русло, а также следить за корректностью их высказываний и математических записей.
В образовательном процессе крайне важно формировать у детей индуктивный подход к поисковой деятельности, демонстрируя естественный процесс «создания» математических знаний. Это подход больше соответствует познавательным возможностям учеников начальной, средней и старшей школы. Он предоставляет возможность экспериментировать с математическими материалами, обращать внимание на числовые и геометрические характеристики, выявлять закономерности и совершать небольшие «открытия».
Рассмотрим пример одной подобной учебной конструкции — последовательности взаимосвязанных заданий, которую мы применяем в процессе обучения восьмиклассников, предоставив при этом необходимые методические разъяснения.
Задание 1.
Верно ли, что
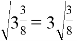
Данная задача по своей сути вводит в заблуждение. Она побуждает многих учеников дать неправильный ответ, так как создает иллюзию, будто тройка может быть извлечена из-под знака корня, хотя это недопустимо. При внесении множителя под знак квадратного корня, этот множитель возводится в квадрат, а при извлечении квадратного корня из результата его выносят. Это и есть основное правило
Тем не менее, равенство (1) действительно является истинным, и убедиться в этом совсем не сложно. Давайте преобразуем его левую сторону:
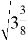
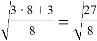
Теперь преобразуем его правую часть:
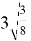
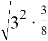
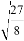
Левая и правая части оказались истинными, таким образом, утверждение является истинным.
Провокационность первого задания моментально уходит, если обратить внимание на то, что тройка, выносимая из-под знака корня, является не множителем, а целой частью смешанного числа
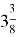
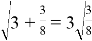
Задание 2. Приведите примеры равенств, аналогичных равенству (1).
Нахождение соответствующих примеров может осуществляться различными способами. В большинстве случаев первоначально применяется метод случайного выбора, то есть выполняют несколько попыток «наобум»:
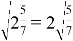
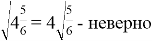
Существует возможность использовать метод исчерпывающего поиска всех возможных вариантов.
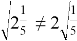
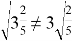
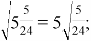
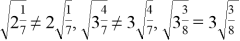
Хотя данная стратегия вызывает некоторый интерес, она вскоре становится однообразной и недейственной.
Уменьшить количество анализируемых альтернатив можно, принимая во внимание характер первоначального равенства, что у
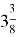
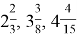
В ходе осуществления определенной стратегии возникает набор искомых равенств:
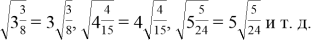
Легко увидеть, что в полученных равенствах целая часть смешанного числа составляет, соответственно, 2, 4, 5 и так далее, что позволяет заключить, что примеров можно привести бесчисленное количество.
В таких ситуациях возникает естественная необходимость обнаружения математической формулы, которая описывает все равенства данного типа. Наиболее простой и увлекательный способ осуществить этот поиск — воспользоваться индуктивным обобщением.
Задание 3. Составьте математическое соотношение, задающее все равенства, аналогичные равенству (1).
Следует отметить, что знаменатель k каждой из дробей, расположенных под корнем, оказывается равным квадрату числителя n за вычетом единицы: 3 = 2 2– 1, 8 = 3 2– 1, 15 = 4 2– 1 и т. д.
В общем виде получаем: k = n
2–
1, тогда смешанное число, которое находится под корнем, следует представлять в следующем формате
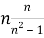
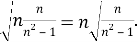
Общее соотношение также можно сформировать, опираясь на следующую характеристику чисел, которые входят в коренные выражения в равенствах (2). В этом случае знаменатель каждой дроби представляет собой произведение двух множителей, где один множитель меньше числителя на единицу, а другой, соответственно, больше числителя на единицу:
3 = 3∙1, 8 = 2 ∙ 4, 15 = 3 ∙ 5 и т. д.
Таким образом, искомое равенство примет следующую форму
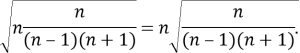
Оно легко преобразуется к виду (3).
Теперь можно с уверенностью сказать, что обнаружены все равенства, подобные равенству (1).
Литература:
1. Брунер Дж., Ольвер Р., Гринфильд П. Исследование развития познавательной деятельности. — М.: Педагогика, 1971.
2. Лэзан. Развитие математической инициативы. — М.: Директ-Медиа, 2014.
3. Пойа Д. Как решить задачу. — 2-е изд. — М.: Учпедгиз, 1961.







