Введение
Интегральные операторы с ядрами типа Бергмана интенсивно исследовались в последние несколько десятилетий. В течение этого периода по этим вопросам уже опубликованы четыре монографии ([1], [2], [3], [4]). Эти исследования в основном проводились в ![]() весовых пространствах аналитических и гармонических функций.
весовых пространствах аналитических и гармонических функций.
В этой статье исследуется поведение этих операторов в пространствах ограниченных в единичном круге функций, для которых n-ная производная (![]() ) по одному направлению (либо по радиусу, либо по углу) удовлетворяет определенным оценкам при приближении к единичной окружности. В данной работе, в частности установили, что если непрерывная функция у которой n-ная производная по одному направлению (либо по радиусу, либо по углу) имеет степенной рост порядка
) по одному направлению (либо по радиусу, либо по углу) удовлетворяет определенным оценкам при приближении к единичной окружности. В данной работе, в частности установили, что если непрерывная функция у которой n-ная производная по одному направлению (либо по радиусу, либо по углу) имеет степенной рост порядка ![]() , то после проектирования на пространство Бергмана, получим аналитическую функцию в единичном круге, удовлетворяющую условию Гельдера порядка
, то после проектирования на пространство Бергмана, получим аналитическую функцию в единичном круге, удовлетворяющую условию Гельдера порядка ![]() в замкнутом круге. Это показывает, что оператор Бергмана улучшает поведение функции довольно существенно.
в замкнутом круге. Это показывает, что оператор Бергмана улучшает поведение функции довольно существенно.
Для изложения основных результатов введем следующие обозначения.
Пусть ![]() — единичный круг на комплексной плоскости
— единичный круг на комплексной плоскости ![]() , φ — некоторая монотонно растущая положительная функция на
, φ — некоторая монотонно растущая положительная функция на ![]() ,
, ![]() — неотрицательное целое число, то есть
— неотрицательное целое число, то есть ![]() , H(D) — множество голоморфных функций в
, H(D) — множество голоморфных функций в ![]() , введем также обозначение
, введем также обозначение
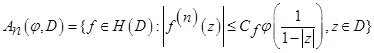 , (1)
, (1)
где ![]() — некоторое положительное число, зависящее только от
— некоторое положительное число, зависящее только от ![]() .
.
Определение. Пусть ![]() — некоторая монотонно возрастающая функция на
— некоторая монотонно возрастающая функция на ![]() , причем
, причем ![]() . Скажем, что функция принадлежит классу
. Скажем, что функция принадлежит классу ![]() , если существует положительное число
, если существует положительное число ![]() , такое что:
, такое что: 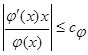 и
и 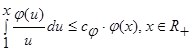 .
.
Через ![]() обозначим ядро типа Бергмана порядка s,
обозначим ядро типа Бергмана порядка s, ![]() — интегральный оператор с ядром типа Бергмана
— интегральный оператор с ядром типа Бергмана ![]() . Таким образом, если
. Таким образом, если ![]() измерима в
измерима в ![]() , при этом
, при этом 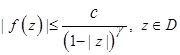 при некоторых γ>0, то интегральный оператор
при некоторых γ>0, то интегральный оператор ![]() , определяем следующим образом:
, определяем следующим образом:
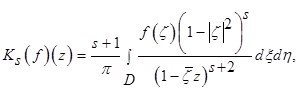 где
где ![]() ,
,
который отображает множество таких функций в множество ![]() .
.
Поэтому если φ удовлетворяет оценке ![]() , при некоторых γ и
, при некоторых γ и ![]() тогда интегральный оператор типа Бергмана отображает пространство
тогда интегральный оператор типа Бергмана отображает пространство ![]() , то есть
, то есть 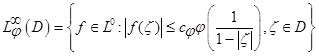 , в пространство
, в пространство ![]() , где
, где ![]() — пространство всех измеримых функций в
— пространство всех измеримых функций в ![]() .
.
Формулировка и доказательство основных результатов статьи
Основными результатами статьи является доказательство следующих двух теорем.
Теорема 1. Пусть функция ![]() интегрируема в
интегрируема в ![]() и такая, что
и такая, что ![]() и
и 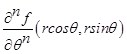 принадлежат
принадлежат ![]() , при некотором
, при некотором ![]() . Тогда
. Тогда ![]() принадлежит классу
принадлежит классу ![]() .
.
Теорема 2. Пусть функция ![]() интегрируема в
интегрируема в ![]() и такая, что
и такая, что ![]() и
и 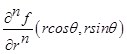 принадлежат
принадлежат ![]() , при некотором
, при некотором ![]() . Тогда
. Тогда ![]() принадлежит классу
принадлежит классу ![]() .
.
Следующая лемма хорошо известна (см. [1]).
Лемма. Пусть s>1, тогда 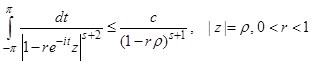 . (2)
. (2)
Перейдем к доказательству основных результатов. Сначала докажем теорему 1. Будем предполагать, что ![]() , поскольку при
, поскольку при ![]() основные идеи доказательства сохраняются, возникают только технические трудности.
основные идеи доказательства сохраняются, возникают только технические трудности.
Итак, пусть ![]() и
и ![]() — достаточно большое положительное число. Докажем, что
— достаточно большое положительное число. Докажем, что ![]() принадлежит пространству
принадлежит пространству ![]() .
.
Имеем
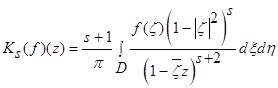 , где
, где ![]() .
.
Найдем производную функции ![]() , переходя к полярным координатам, получим:
, переходя к полярным координатам, получим:
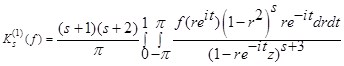 .
.
Рассмотрим внутренний интеграл 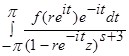 , проинтегрируем его по частям, получим:
, проинтегрируем его по частям, получим:
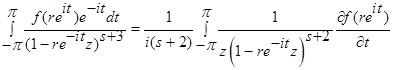
В последнем равенстве использовали 2π-периодичность подынтегральной функции.
Итак, 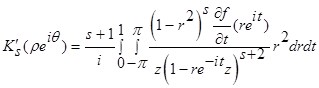
Пусть ![]() . Тогда применив оценку (1), получим:
. Тогда применив оценку (1), получим:
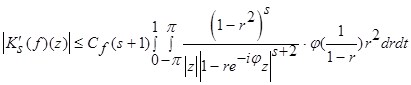 .
.
Следовательно, 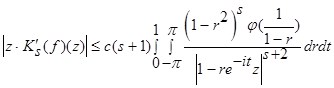 .
.
Для оценки внутреннего интеграла применим Лемму:
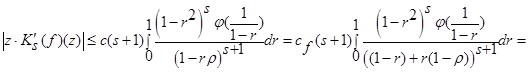
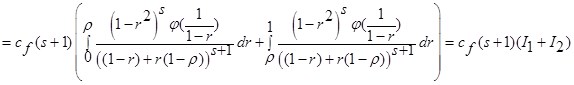 .
.
Оценим каждый интеграл по отдельности.
Так как ![]() интеграл по интервалу
интеграл по интервалу ![]() , то на этом интервале
, то на этом интервале ![]() , то
, то ![]()
![]() , тогда:
, тогда:
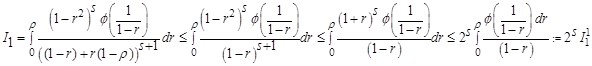
Перейдем к оценке интеграла![]() , имеем:
, имеем: 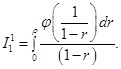
Сделаем замену переменных: ![]() , тогда:
, тогда: 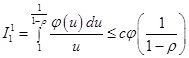 . В последней оценке мы воспользовались условием на
. В последней оценке мы воспользовались условием на ![]() .
.
Так как ![]() — интеграл по интервалу
— интеграл по интервалу ![]() , то
, то ![]() , то есть
, то есть ![]()
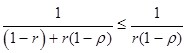 .
.
Поэтому:
![]()
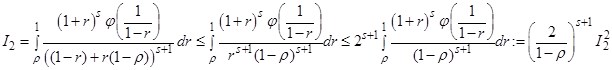
Перейдем к оценке последнего интеграла, для этого сделаем замену переменных: ![]() тогда:
тогда: ![]()
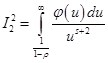 .
.
Будем предполагать, что s — достаточно большое число, ![]() . Интегрируя по частям получим:
. Интегрируя по частям получим:
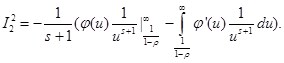
Поскольку ![]() ,то
,то ![]() при
при ![]() , поэтому получим:
, поэтому получим:
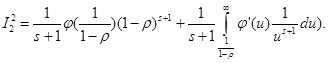
Следовательно:
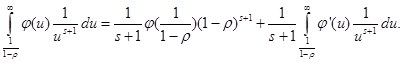
Отсюда имеем:
![]()
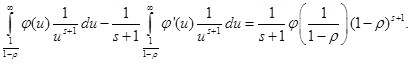 (**)
(**)
Поэтому:
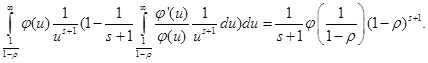
Пусть теперь s удовлетворяет условию ![]() , тогда:
, тогда:
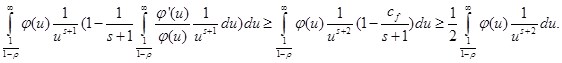
Учитывая (**), получаем: ![]() , следовательно:
, следовательно:
![]() .
.
Объединяя оценки ![]() и
и ![]() , получаем доказательство теоремы:
, получаем доказательство теоремы: 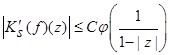 .
.
Теорема доказана.
Доказательство теоремы 2 проводится аналогично доказательству теоремы 1, но при этом учитывается, что под интегралом стоит функция ![]() с достаточно большим значением
с достаточно большим значением ![]() . Аналогично как при доказательстве теоремы 1 мы получим утверждение теоремы 2.
. Аналогично как при доказательстве теоремы 1 мы получим утверждение теоремы 2.
Замечание.
В монографии [5] (стр. 252) установлено, что если функция принадлежит Гёльдеровскому классу непрерывных функций, то ![]() так же принадлежит этому классу. В отличие от этой работы теоремы 1,2 устанавливают, что не только Гёльдеровские классы непрерывных функций отображаются в Гёльдеровские классы аналитических функций, но и более общие классы. То есть, если
так же принадлежит этому классу. В отличие от этой работы теоремы 1,2 устанавливают, что не только Гёльдеровские классы непрерывных функций отображаются в Гёльдеровские классы аналитических функций, но и более общие классы. То есть, если ![]() принадлежат классу
принадлежат классу ![]() , то
, то ![]() .
.
Литература:
1. Djrbshian M. M., Shamoyan F. A. Topics in theory of ![]() spaces, Teubner — Verlag, Leipzig, 1988, pp.200.
spaces, Teubner — Verlag, Leipzig, 1988, pp.200.
2. H. Hedermalm, B. Korenblum, K. Zhu. Theory of Bergman spaces, Springer — Verlag New York, 2000.
3. P. L. Duren, A. S. Sсhuster, Bergman spaces, Amer. math. Soc. Providence, 2004, pp. 100.
4. K. Seip Interpolating and Sampling in spaces of analytic functions, Amer. math. Soc. Providence, 2004, pp. 180.
5. K. Zhu. Spaces of Holomorphic Functions in the Unit Ball, Springer — Verlag New York, 2005.







