Анализ процедур генерации ключей криптографических алгоритмов. Программная реализация теста на оценку энтропии для равномерно распределенных последовательностей Draft SP 800-90b

Основной алгоритм.

Данный тест оценивает энтропию на выходе генератора равномерно распределенной величины, базирующийся на подсчете среднестатистического выходного значения, полученного в результате нескольких наблюдений [1]. Оценка энтропии генератора равномерно распределенной величины — простой процесс. Она используется для обеспечения верхней границы вероятности в 99 %, pmax, что наиболее распространенные значения в выборке будут лежать в этих пределах. Также эта величина используется и для оценки минимального значения энтропии на выходе генератора [1].

Алгоритм выполнения теста следующий:

Получаем выборку из N элементов.

а)                  Находим наиболее часто встречающееся значение в выборке;

б)                 Считаем количество совпадений с этим значением, пусть это будет C_max;

в)                 Pmax = C_max/N;

г)                  Считаем С_bound=C_MAX+2.3;

д)                 H=-log₂(C_bound/N);

е)                  Пусть W будет количество бит в каждом элементе выборки (т. е. размер элемента);

ж)                min(W,H) — это нижняя граница оценки энтропии.

Например, если набор данных {0, 1, 1, 2, 0, 1, 2, 2, 0, 1, 0, 1, 1, 0, 2, 2, 1, 0, 2, 1}, наиболее часто встречающееся значение — 1, C_MAX=8 и pmax = 0.4.

C_BOUND = 8 + 2.3= 13.04.

H = –log₂(0.652) = 0.186.

W = 3.                       

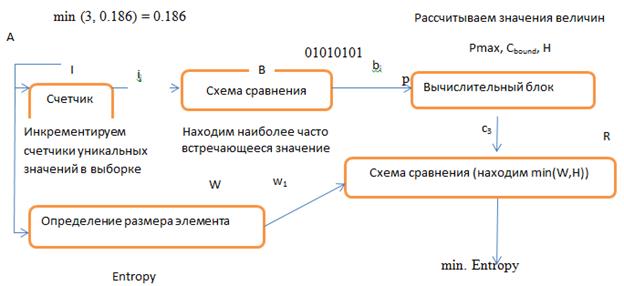
Рис. 1. Абстрактный автомат алгоритма теста на оценку энтропии для равномерно распределенных последовательностей

Абстрактный автомат получим, если укажем алфавит A, B, C, I, R и программу P, как совокупность команд вида: i_i,a_j ®b_x,c_y.

В нашем случае:

A = {a₁,a_2,a₃, a₄… a_N}, B={b₁}, C={ c₁,c_2, c₃}, I={i₁,i₂,…,i_n}, R={r₁}

δ: IxA ®BxC ={a₁i₁ ® b₁c₁, a₂i₂ ® b₁c₁, a_ni_n ® b₁c_1, a₁i₁ ® b₁c₂, a₂i₂ ® b₁c₂, a_ni_n ® b₁c_2, a₁i₁ ® b₁c₃, a₂i₂ ® b₁c₃, где w₁c₃®r₁}

Имеем следующий абстрактный автомат, как математическую модель схемы оценки минимальной энтропии в равномерно распределенной последовательности.

Программная реализация.

Литература:

1.                  http://csrc.nist.gov/publications/PubsSPs.html «DRAFT — SP800–90b».