Введение
На современном этапе демографические модели используются в социально-экономических науках как инструмент анализа характеристик населения и построение демографических прогнозов. Анализ демографических моделей позволяет спрогнозировать различные варианты социально-экономических явлений, а так же целенаправленно воздействовать на их развитие, корректировать в необходимую для страны сторону.
“Сравнивая полученные в результате моделирования величины и те параметры демографических процессов, например, численности и возрастно-полового состава населения в том или ином регионе, которые желательно с социально-экономических позиций для общества в перспективе, можно выявить степень расхождения желаемых и возможных характеристик демографических процессов” [1]. Таким образом, актуальность данной работы состоит в важности вышеуказанных категорий для регулирования демографических процессов.
Приведенная в работе модель включает рождение, смертность внутри населенного пункта, прибытие людей извне (иммиграцию) и отъезд за пределы населенного пункта (эмиграцию). Под малым населенным пунктом подразумевается населенный пункт с численностью населения меньше 100 тыс. человек. Данная математическая модель не рассматривает большие притоки или потери населения, происходящие, например, при слиянии двух или более населенных пунктов, войнах или эпидемиях.
Целью данной работы является построение адекватной математической модели позволяющей анализировать возрастно-половой состав населения. Методом исследования является имитационное стохастическое моделирование.
Математическая модель
Построим формальную математическую модель численности населения малого населенного пункта в терминах семимартингальных точечных процессов с непрерывным временем (основные определения и термины для описания семимартингалов см в [2]). Обозначим 
— число людей в населенном пункте в возрасте до 
лет (включая , 
) в момент времени 
. Примем следующие обозначения: процессы с индексом “m” относятся к мужчинам; ”f” к женщинам, а без индекса — для представителей обоих полов. Таким образом,
(1)
Тогда число людей в возрастном диапазоне 
(
) в момент времени t равно 
.
Обозначим 
точечный процесс, считающий количество родившихся на территории населенного пункта людей, к моменту времени t. Пусть компенсаторы процессов 
и 
равны
(2)
где 
— плотность распределения вероятности рождения ребенка, женщиной в возрасте лет, 
— математическое ожидание числа детей, которое может родиться в населенном пункте в момент времени 
. Другие способы подсчета математического ожидания числа детей в двуполовых моделях подробно рассматривается в работах [3, 4]. 
— коэффициент рождаемости, зависящий от уровня благосостояния в населенном пункте, 
; 
, 
— весовые коэффициенты, отвечающие за рождение мальчиков и девочек,
, 
(3)
Обозначим 
число людей, родившихся на территории населенного пункта и в момент времени () имеющих возраст не более x лет (). Пусть процессы 
, 
и 
равны
(4)
где 
.
Помимо естественного прироста населения в результате рождения в населенном пункте имеет место поступление извне. Обозначим 
точечный считающий процесс числа прибывших в населенный пункт. Пусть компенсаторы процессов 
, 
и равны
(5)
где 
, 
— интенсивность въездов в населенный пункт мужчин и женщин в возрасте x лет в момент времени t, соответственно.
(6)
— максимальный возраст иммигрировавших в момент времени s, при котором, к моменту времени их возраст будет не больше лет, см рисунок 1 (на рисунке верхнее ребро трапеции описывается уравнением (6)).
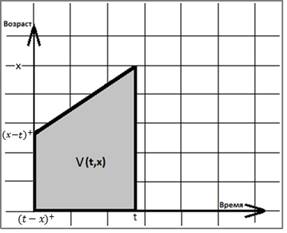
Рис. 1. Область определения 
компенсаторов процессов иммиграции, эмиграции и смерти
Обозначим 
считающий процесс числа умерших до достижения возраста x лет; компенсаторы для процессов 
, 
и зависят от численности населения, и равны
(7)
где 
, 
— плотность распределения вероятностей смерти мужчин и женщин в возрасте x лет в момент времени t, соответственно.
И эмиграции людей из населенного пункта 
, которая также зависит от численности населения
(8)
где 
, 
— плотность распределения вероятностей смерти мужчин и женщин в возрасте x лет в момент времени t, соответственно.
Таким образом, численность населения в момент времени t в возрасте не большем x лет, равна
(9)
Исследование модели
Данная математическая модель позволяет оценивать некоторые социальные показатели, такие как коэффициент рождаемости в населенном пункте, отношение рождаемости мальчиков к девочкам и т. д. на основе имеющихся данных. Ниже приводятся оценки коэффициента рождаемости в населенном пункте.
Предложение. Пусть в каждый момент времени 
известными являются величины , 
, 
для 
, а также известен вид функции (10)
(10)
моменты времени 
, 
такие, что 
при и 
, а также известны 
, 
. Зафиксируем 
и обозначим 
. Тогда 
равно
(11)
где 
.
Доказательство.
Рассмотрим процесс
=
=
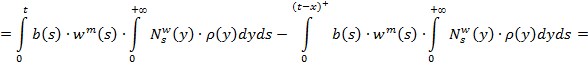
Аналогично,
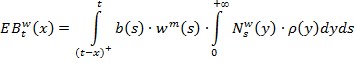
С учетом условия (3), в момент времени 
, получаем
=
(12)
=
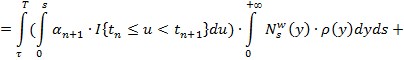
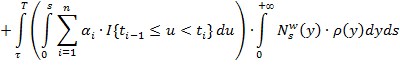
Откуда следует,
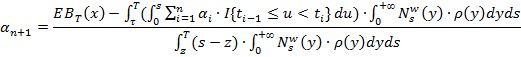
где . И, окончательно
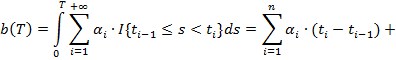
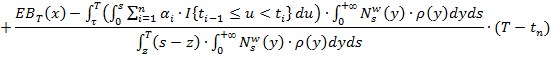
Следствие. При 
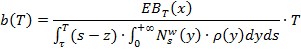
Рассмотрим численные способы оценки при известных дополнительных условиях на функцию . Пусть в каждый момент времени известными являются величины , , для 
, а также известен вид функции (10); моменты времени , такие, что при и , а также , . И пусть дополнительно известно, что функция монотонно возрастает и ограничена на 
.
Зафиксируем некоторый и обозначим . Обозначим 
. Очевидно, что 
, а — неотрицательная, монотонно возрастающая функция, ограниченная на . Воспользуемся леммой для второй теоремы о среднем для определенного интеграла [3]
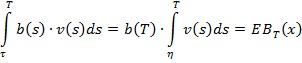
где 
. И
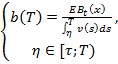(13)
Полученное уравнение (13) может иметь более одного корня, однако на практике зачастую бывают, известны некоторые ограничения на значение . К таким ограничениям могут относиться 
, где 
, 
— действительные числа. Либо, если известно значение 
при 
, тогда в силу монотонности 
.
Заключение
Построена математическая модель численности населения небольшого населенного пункта в виде семимартингального точечного процесса с непрерывным временем. Приведены способы оценивания неизвестных параметров, на примере коэффициента рождаемости.
Прикладное значение работы состоит в использовании полученных результатов к исследованию сложившейся и прогнозирования будущей демографической ситуации, в небольших населенных пунктах, численностью до ста тысяч человек.
Литература:
1. Социогид. http://www.socioguru.ru/sgurus-634–1.html (Дата обращения: 23.07.2013)
2. Липцер Р. Ш. Статистика случайных процессов / Р. Ш. Липцер, А. Н. Ширяев. — М.: Наука, 1974. — 696 стp.
3. Kendall D. G., Stochastic process and population growth, J. Roy. Statist. Soc. (London) B10 (1948), 230–264.
4. Goodman L., Population growth of the sexes, Biometrics, 9 (1953), 212–225.
5. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления (том 2) / Г. М. Фихтенгольц. — М.: ФИЗМАТЛИТ, 2001. т.2–810 с.
