В работах [1] … [3] рассмотрено математическое моделирование линейных асинхронных двигателей при помощи магнитных схем замещения с классическим типом обмотки. В данной работе представлена математическая модель линейного асинхронного двигателя с намоткой обмотки через спинку ярма индуктора. Такой тип укладки обмотки позволит управлять напряжением в проводниках каждого паза и, кроме того, приводит к существенному изменению конфигурации заполнения элементов матриц [4], [5]. Работа адресована студентам, поэтому дана без сокращений.
На рис.1,а показан линейный асинхронный двигатель с одной парой полюсов (2р = 2, Z1 = 12) с укладкой обмотки через спинку ярма статора. На рис. 1,б дана его магнитная схема замещения.
Запишем основные уравнения для «n»-ого участка схемы замещения.
Баланс магнитных напряжений магнитной цепи
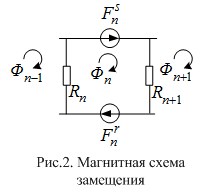
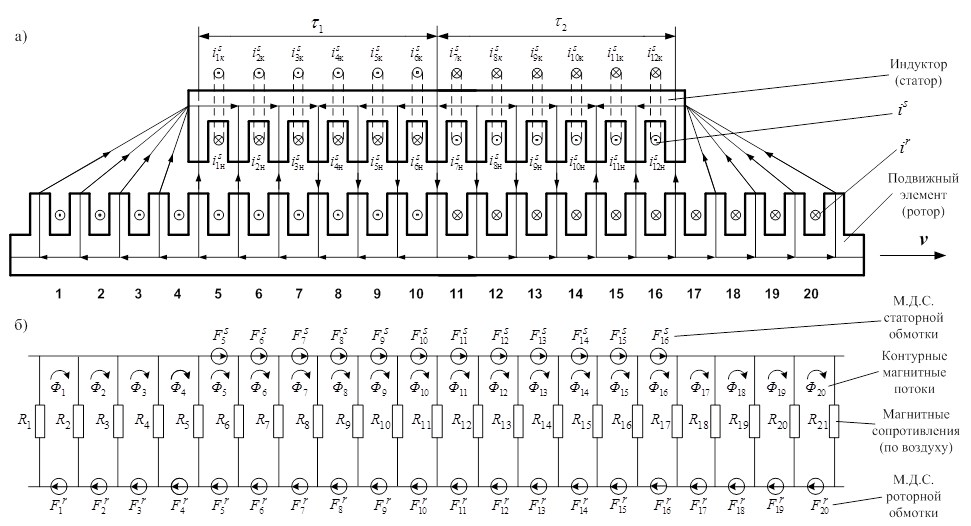
Рис. 1. а) Линейный асинхронный двигатель (2р = 2, Z1 = 12); б) магнитная схема замещения.
![]() — контурные магнитные потоки;
— контурные магнитные потоки;
![]() — магнитные сопротивления воздушных участков;
— магнитные сопротивления воздушных участков;
![]() — магнитодвижущая сила, созданная статорным током
— магнитодвижущая сила, созданная статорным током ![]() , протекающим по всем проводникам паза (
, протекающим по всем проводникам паза (![]() );
);
![]() — М. Д. С. тока ротора в стержне (
— М. Д. С. тока ротора в стержне (![]() );
);
![]() – в шунтирующих зонах.
– в шунтирующих зонах.
Баланс М. Д. С. для «n»-го участка имеет следующий вид:
![]() .
.
Отсюда ток в стержне ротора определится по следующему выражению:
![]() . (1)
. (1)
Уравнение баланса напряжений электрической цепи ротора
![]() (2)
(2)
Выразим производные во времени через конечные разности:
![]() ,
,
где n — номер зубцового деления;
k — номер шага разбиения по времени.
В формуле (2) скорость подвижного элемента принимаем равным ![]() и в пределах «k» интервала считается постоянным.
и в пределах «k» интервала считается постоянным.
Производные по пространственной координате «х» выразим через центральные конечные разности:
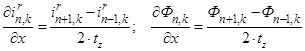 .
.
С учетом вышеприведенных замечаний уравнение (2) примет следующий вид:
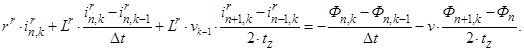 (3)
(3)
Исключим из уравнения (3) токи в роторе. Для этого подставим выражение (1) в уравнение (3) и получим:
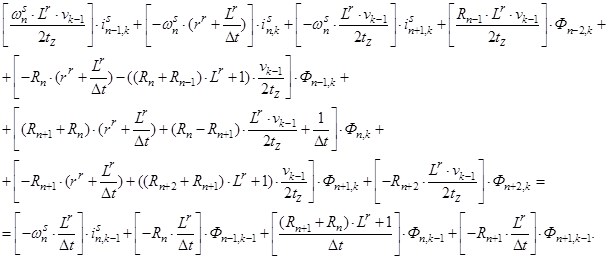 (4)
(4)
Это уравнение может быть реализовано при произведении матрицы А, элементы которой записаны в квадратных скобках, на матрицу-столбец X, состоящей из потоков (Ф) и токов статорной обмотки. Правая часть уравнения (4) формирует первые двадцать элементов матрицы-столбца свободных членовS в (k-1) момент времени. Остальные двенадцать будут сформированы из баланса напряжений статорной обмотки. Матрица-столбец Х сформирована из первых двадцати элементов, которые соответствуют потокам Ф1,Ф2, …, Ф20, а с 21 по 32 — токам is1, …, is12. Общий вид матриц при числе полюсов 2р = 2 и общем числе пазов индуктора (статора) Z1 = 12 приведен на рис.3.
Введем следующие обозначения:
- Магнитные сопротивления в шунтирующих зонах:
R1 = R2 = R20 = R21 = 500•Rδ;
R3 = R19 = 50•Rδ;
R4 = R18 = 5•Rδ.
- Магнитные сопротивления в индукторной зоне:
R5 = R6 = … = R16 = R17 = Rδ.
- Элементы матрицы А, перемножаемые на потоки матрицы-столбца Х:
![]()
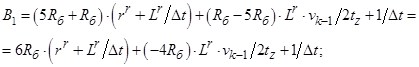
![]()
![]()
![]()
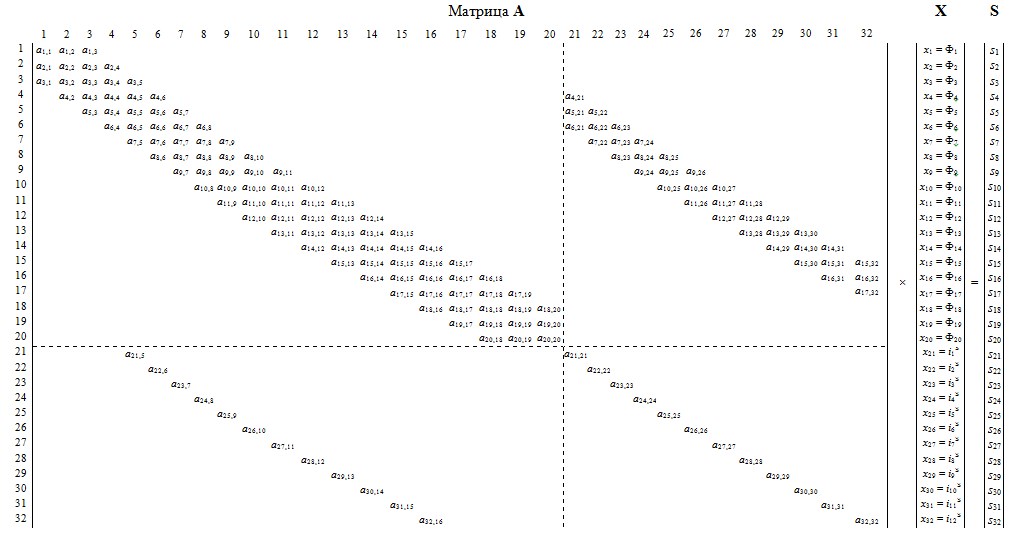
Рис. 3. Общий вид матриц A, X и S.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
- Элементы матрицы А, перемножаемые на токи i1, …, i12 матрицы Х:
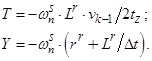
- Элементы матрицы-столбца свободных членов S:
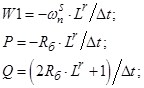
![]()
Уравнение (4) позволит определить для первых двадцати строк элементы матрицы А и с первый по двадцатый элементы матрицы-столбца S, для этого последовательно зададимся n:
n = 1.
![]()
Запишем элементы матрицы А:
![]() ;
; ![]() ;
; ![]() .
.
В правой части сформирован элемент ![]() матрицы-столбца S:
матрицы-столбца S:
![]()
Примечание: Вначале матрица А предстанет «пустой» и после каждой операции n = … определятся постепенно элементы для каждой строки и только в конце всех операций матрица А предстанет перед читателем в том виде как она дана на рис. 3. Но эта «пустая» матрица А уже должна быть подготовлена. Эта «пустая» форма направляет, выступает «организующим началом» по поиску элементов в каждой строке.
В этом случае при n = 1 определились элементы первой строки. Найденные коэффициенты вписываем в матрицу А. В дальнейшем становится понятным алгоритм заполнения матрицы.
n = 2.
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
![]()
n = 3.
![]()
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 4.
![]()
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]() .
.
n = 5.
![]()
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 6.
![]()
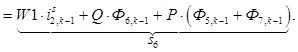
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 7.
![]()
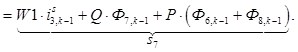
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 8.
![]()
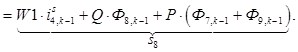
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 9.
![]()
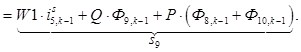
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 10.
![]()
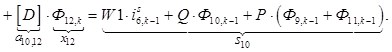
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 11.
![]()
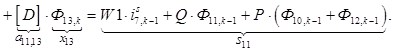
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 12.
![]()
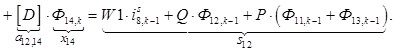
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 13.
![]()
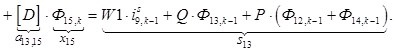
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 14.
![]()
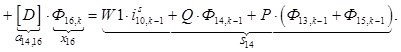
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 15.
![]()
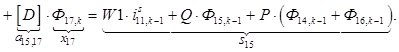
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 16.
![]()
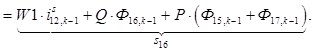
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 17.
![]()
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 18.
![]()
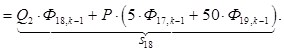
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 19.
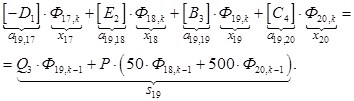
![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
n = 20.
![]()
![]() ;
; ![]() ;
; ![]()
![]()
Остальные элементы матрицы А (n = 21, …, 32) и соответствующие элементы матрицы-столбца S определяются из баланса электрических напряжений обмоток статора [2].
В данной работе принято управление напряжением обмотки каждого паза (Z1 = 12), следовательно, необходимо задать двенадцать напряжений. В качестве одного из вариантов примем синусоидальные напряжения со сдвигом на π/6:
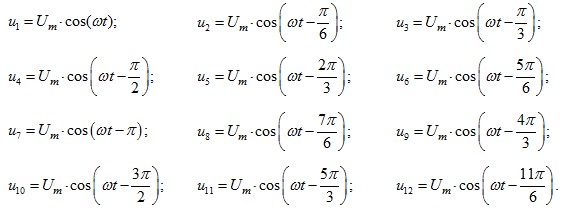
Рассмотрим баланс напряжений для первой обмотки.
![]() ,
,
где ![]() — число витков паза (обмотки);
— число витков паза (обмотки);
![]() — сопротивление обмотки, проходящей через спинку ярма;
— сопротивление обмотки, проходящей через спинку ярма;
![]() – индуктивность обмотки первого паза.
– индуктивность обмотки первого паза.
Выразим производные через конечные разности:
![]() ;
; ![]() .
.
Тогда после подстановки получим:
![]() .
.
Преобразуем выражение к виду:
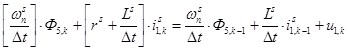 .
.
Обозначим:
![]() ;
; ![]() .
.
Тогда для элементов двадцать первой строки матрицы А и двадцать первого элемента матрицы-столбца S (n = 21):
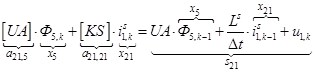 .
.
Отсюда элементы матрицы А: ![]() ;
; ![]() .
.
Двадцать первый элемент ![]() матрицы-столбца S:
матрицы-столбца S:
![]() .
.
Аналогично для n = 22, …, 32 запишем:
n = 22. 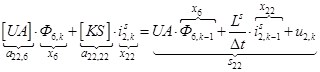 .
.
![]() ;
; ![]()
![]()
n = 23. 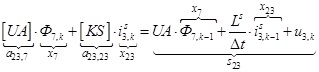 .
.
![]()
![]()
![]()
n = 24. 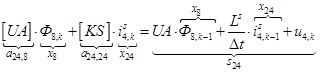 .
.
![]()
![]()
![]()
n = 25. 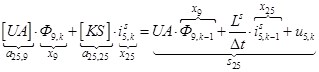 .
.
![]()
![]()
![]()
n = 26. 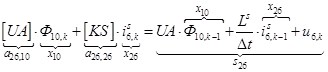 .
.
![]()
![]()
![]()
n = 27. 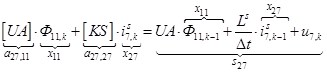 .
.
![]()
![]()
![]()
n = 28. 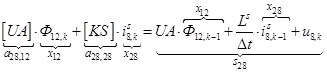 .
.
![]()
![]()
![]()
n = 29. 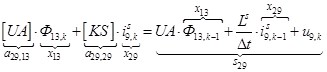 .
.
![]()
![]()
![]()
n = 30. 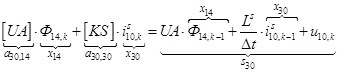 .
.
![]()
![]()
![]()
n = 31. 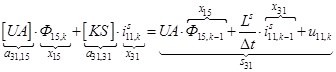 .
.
![]()
![]()
![]()
n = 32. 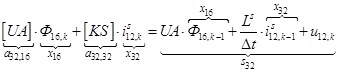 .
.
![]()
![]()
![]()
Окончательно, матрица А примет следующий вид, удобный для программирования в MATLAB:

Неизвестные переменные (потоки и токи в статорной обмотке) в k-й момент времени определяются в результате следующей операции с матрицами:
X=A-1·S,
Далее, подставляя в уравнение (1) n = 1…20, определяем токи в роторе:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Электромагнитные усилия на зубцовом делении определяются по следующим формулам:
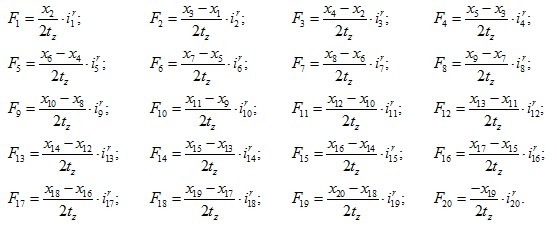
Суммарное усилие: ![]() .
.
Скорость в k-й момент времени: ![]()
Произведем построение математической модели асинхронного двигателя методом Гаусса-Жордана с использованием языка программирования MatLab. Ниже приведен пример кода:









Результаты моделирования представлены на рис.4.
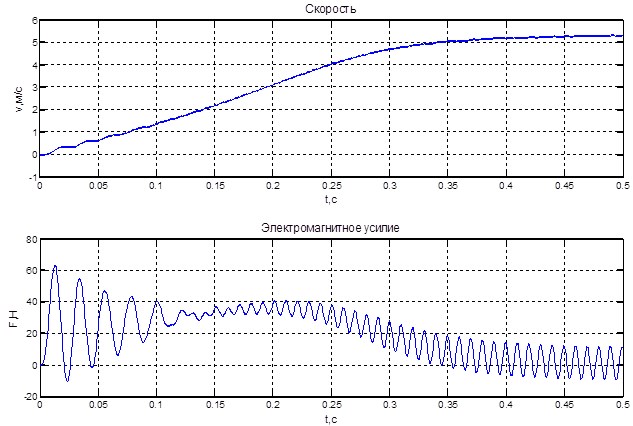
Рис. 4. Результат моделирования асинхронного двигателя в режиме прямого пуска
Литература:
1. Сарапулов Ф. Н., Емельянов А. А., Иваницкий С. В., Резин М. Г. Исследование электромеханических переходных процессов линейного асинхронного короткозамкнутого двигателя // Электричество. — 1982. — № 10. — С. 54–57.
2. Емельянов А. А., Богатов Е. А., Клишин А. В., Медведев А. В., Симонович В. Г. Математическая модель линейного асинхронного двигателя на основе магнитных схем замещения // Молодой ученый. — 2010. — № 5. — С.14–22.
3. Емельянов А. А., Медведев А. В., Богатов Е. А., Кобзев А. В., Бочкарев Ю. П. Программирование линейного асинхронного двигателя в MATLAB // Молодой ученый. — 2013. — № 3. — С. 129–143.
4. Емельянов А. А., Медведев А. В., Кобзев А. В., Бесклеткин В. В., Козлов А. М. Моделирование асинхронного двигателя с укладкой обмотки статора (Z1 = 12) через спинку ярма // Молодой ученый. — 2013. — № 7. — С. 12–27.
5. Емельянов А. А., Медведев А. В., Кобзев А. В., Евдокимов О. В., Габзалилов Э. Ф., Авдеев А. С. Моделирование асинхронного двигателя с укладкой обмотки статора (Z1 = 6) через спинку ярма // Молодой ученый. — 2013. — № 6. — С. 1–11.
6. Ануфриев И. Е. и др. MATLAB 7 / Ануфриев И. Е., Смирнов А. Б., Смирнова Е. Н.. — СПб.: БХВ-Петербург, 2005. — 1104 с.







