В статье предложена методика прогнозирования качества игры игрока НБА. Рассмотрено использование языка R для анализа данных, в частности, при анализе данных игроков Национальной Баскетбольной Ассоциации. Разработана и протестирована модель прогнозирования успешности игры того или иного игрока на будущие сезоны.
Ключевые слова: язык R, регрессионный анализ, баскетбол, национальная баскетбольная ассоциация, прогнозирование успешности игрока.
The article proposes a method for predicting the quality of an NBA player's game. The use of the R language for data analysis is considered, in particular, when analyzing data on National Basketball Association players. A model for predicting the success of a particular player's game for future seasons is developed and tested.
Keywords: R language, regression analysis, basketball, national basketball association, predicting player success.
Сегодня, спорт перестал быть просто спортом: стриминговые сервисы и телеканалы борются за права трансляций соревнований, богатейшие компании спонсируют спортивные клубы, а сами спортсмены зачастую зарабатывают на рекламных контрактах больше, чем за достижения в спорте.
Одним из самых медийных видов спорта является баскетбол, подаривший миру Майкла Джордана, Шакила О’Нила и Леброна Джеймса — звезд, о которых слышал практически каждый человек вне зависимости от того, увлекается он баскетболом или нет. Этот вид спорта популярен на всех континентах, что делает его одним из самых равномерно распространенных на планете.
Национальная баскетбольная ассоциация, НБА — мужская профессиональная баскетбольная лига Северной Америки, в частности, США и Канады. Входит в четвёрку главных профессиональных спортивных лиг Северной Америки, наряду с НХЛ, МЛБ и НФЛ. Поэтому анализ данных об игроках этой ассоциации является актуальной задачей для баскетбольных клубов, болельщиков и различных букмекерских контор [1].
Для анализа факторов, показывающие качества игры того или иного игрока, была создана модель на языке R, с возможностью прогноза показателей успешности игрока на будущие сезоны. R-язык программирования, созданный специально для статистического анализа данных. На другие популярные языки R абсолютно не похож. У него свой уникальный синтаксис, функции и принципы работы. У языка R чёткая сфера применения — статистические вычисления, анализ данных и машинное обучение. Его создавали специально для этих задач, и для других он не подходит. Однако, R не только язык для анализа данных, но и целая рабочая среда, куда уже встроены готовые методы статистического анализа и инструменты для визуализации [2].
В качестве исследуемых данных мы использовали «Fantasy Basketball Statistics NBA Player Statistics (2024)». Это набор данных, содержащий рейтинг игроков Национальной баскетбольной лиги США. Эти статистические данные были взяты за сезон 2024–2025 года. Каждая строка состоит из игрока и его статистики на сезон НБА 2024–2025 гг. Статистика включает в себя все основные данные, такие как очки, передачи, подборы и т. д. Данные находятся на сайте fantsypros.com [3]. Файл с входными данными содержит 549 строк-информации об игроках и 14 показателей (рис. 1).
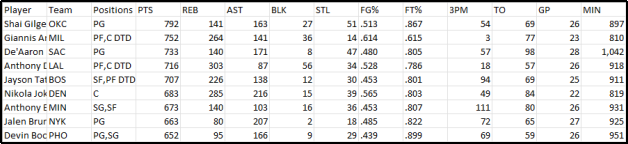
Рис. 1. Формат входных данных
Входными переменными csv файла являются:
- Player (Имя игрока, текст)
- Team (Команда игрока, текст)
- Positions (Позиции игрока, текст)
- PTS (Очки игрока, число)
- REB (Количество подобранных мячи, число)
- AST (Количество передач перед успешным броском, число)
- BLK (Количество удачных блоков, число)
- STL (Количество удачных перехватов мяча, число)
- FG % (Процент удачных бросков к общему числу бросков, число)
- FT % (Процент удачных штрафных бросков к общему числу штрафных бросков, число)
- 3PM (Количество бросков из трёхочковой зоны, число)
- TO (Количество потерянных мячей, число)
- GP (Количество игр, число)
- MIN (Количество минут в игре, число)
Проведем статистический анализ столбцов. Основную информацию о выборке можно получить, используя функцию summary. Эта функция сообщает минимальное и максимальное значения, медиану, среднее, первый, и третий квартиль (табл. 1).
Таблица 1
Статистический анализ файла
|
Столбец |
Min. |
1 st Qu. |
Median |
Mean |
3 rd Qu. |
Max |
|
PTS |
0.0 |
65.0 |
315.0 |
472.2 |
665.0 |
2335.0 |
|
REB |
0.0 |
38.0 |
128.0 |
171.3 |
260.0 |
905.0 |
|
AST |
0.0 |
14.0 |
56.0 |
93.15 |
117.0 |
677.0 |
|
BLK |
0.0 |
3.0 |
10.0 |
18.76 |
24.0 |
196.0 |
|
STL |
0.0 |
6.0 |
23.0 |
29.21 |
46.0 |
125.0 |
|
FG % |
0.0 |
0.396 |
0.438 |
0.429 |
0.485 |
1.0 |
|
FT % |
0.0 |
0.635 |
0.75 |
0.6827 |
0.83 |
1.0 |
|
3PM |
0.0 |
3.0 |
25.0 |
46.69 |
75.0 |
299.0 |
|
TO |
0.0 |
11.0 |
40.0 |
53.19 |
77.0 |
305.0 |
|
GP |
0.0 |
18.0 |
47.0 |
40.38 |
61.0 |
73.0 |
|
MIN |
0 |
277 |
871 |
924 |
1558 |
2556 |
Для начала используем кластеризацию для разделения игроков по их рейтингу и количеству минут в игре. Данный метод позволит выделить игроков, показывающих высокие показатели, игроков, которые играют средне, и игроков, играющих плохо. Это должно помочь клубам в выборе покупки перспективных игроков.
Для этого используем метод k-средних — наиболее популярный метод кластеризации, изобретённый в 1950-х годах математиком Г. Штейнгаузом и почти одновременно С. Ллойдом [4]. Действие алгоритма таково, что он стремится минимизировать суммарное квадратичное отклонение точек кластеров от центров этих кластеров (1):

где k — число кластеров,



Результат работы программы представляет собой три кластера характеризующий игроков как: «Высокие показатели», «Средние показатели», «Низкие показатели». Чем больше минут игрок провел в игре, и чем больше его рейтинг, тем выше его показатели (рис. 2).
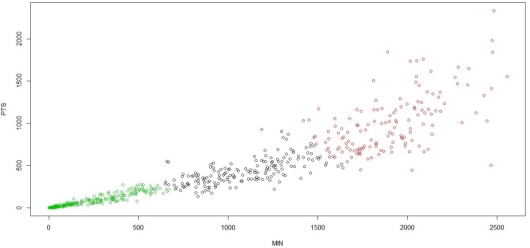
Рис. 2. Кластеризация игроков (3 кластера)
Далее используем линейную регрессию, чтобы иметь возможность предсказывать будущие успехи игрока на основе имеющихся факторов. Линейная регрессия — это используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной y от другой или нескольких других переменных (факторов, регрессоров, независимых переменных) x с линейной функцией зависимости.
Регрессионная модель (2):

где b — параметры модели,



где


Основываясь на этом, построим модель, которая позволяла бы предсказания рейтинга игрока на основе параметров. Результат программы представлен на рис. 3.
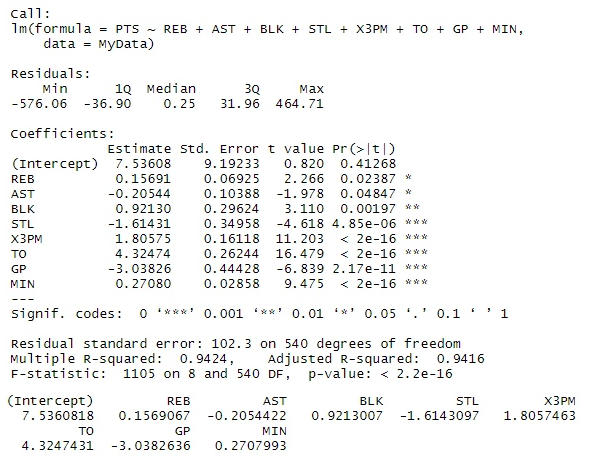
Рис. 3. Множественная регрессия и коэффициенты регрессии
Из результата работы программы видно, что коэффициент детерминации R-squared равен 0.9424. Чем ближе к 1, тем ярче выражена зависимость. Значение скорректированного коэффициента детерминации Adjusted R-squared равно 0.9416, значит зависимость является ярко выраженной. Чем больше значение параметра F-statistic, тем лучше. F-statistic = 1105. Если критерий t-value, больше 2, то фактор является значимым для модели. Для нашей модели значимыми факторами являются факторы: REB, BLK, X3PM, TO, MIN.
Вероятность истинности нуль гипотезы p-value, которая гласит, что независимые переменные не объясняют динамику зависимой переменной, и, при p-value равным 2.2e -16 нуль гипотеза является ложной, что говорит о том, что связь между факторами регрессии и зависимой переменной существует.
Создадим новый набор данных с новыми показателями игрока, повторяющими реальные показатели (рис. 4). После чего предскажем значение показателя «PTS» по предлагаемой модели, а также проверим ее адекватность.

Рис. 4. Набор данных с новыми значениями
Сравним результат с реальным игроком, данные которого совпадают с заданными (рис. 5). PTS игрока равен 256, предсказанный PTS — 261.5036. Отклонение составило 5,5036.

Рис. 5. Реальные данные игрока
Проведем еще один анализ модели предсказания PTS игрока. Зададим исходные значения — (150,60,15,45,20,35,40,600). Для этих данных модель предсказывает PTS = 188.3511.
Таким образом, разработанная модель работоспособна и позволяет предсказывать успешность игрока в следующем сезоне, на основе имеющихся показателей. Построенная модель была протестирована на работоспособность и показала хороший результат по прогнозированию показателей игрока с минимальным отклонением.
Литература:
- Самые популярные виды спорта [Электронный ресурс] // — Режим доступа: https://legalbet.ru/prosport/samie-populyarnie-vidi-sporta/ (дата обращ. 20.12.2024)
- Язык программирования R: что делает его таким важным для анализа данных [Электронный ресурс] // — Режим доступа: https://practicum.yandex.ru/blog/chto-takoe-yazyk-r/ (дата обращ. 20.12.2024)
- FantasyPros [Электронный ресурс] // — Режим доступа: https://www.fantasypros.com/nba/stats/overall.php (дата обращ. 20.12.2024).
- Метод k-средних [Электронный ресурс] // Википедия — Режим доступа: https://ru.wikipedia.org/wiki/Метод_k-средних (дата обращ. 20.12.2024).
- Линейная регрессия [Электронный ресурс] // Википедия — Режим доступа: https://ru.wikipedia.org/wiki/Линейная_регрессия (дата обращ. 20.12.2024).







