Поиск кратчайшего пути в графе методом оптимизации



В данной статье автор предлагает новую методику поиска кратчайшего пути в графах.

Ключевые слова: графы, теория, кратчайший, путь, математика

В данной работе я хочу показать способ поиска кратчайшего пути между вершинами графа, предполагающий упрощение графа до набора простейших графов, каждый из которых представляет из себя идущие друг за другом в одну линию ребра, изначально являющиеся ребрами первоначального графа.

При изучении основных методик поиска кратчайшего пути в графах, мной были выделены 7 основных алгоритмов:

1. Алгоритм Дейкстры
2. Алгоритм Беллмана — Форда
3. Алгоритм поиска A*
4. Алгоритм Флойда — Уоршелла
5. Алгоритм Джонсона
6. Алгоритм Ли (волновой алгоритм)
7. Поиск кратчайшего пути на основе алгоритма Килдала

Указанные алгоритмы отлично выполняют свою задачу, удобно накладываются на концепцию автоматизации при помощи различных языков программирования, но плохо применимы при необходимости ручного поиска кратчайшего пути в целях обучения или при работе в полевых условиях/необходимости быстрого расчета в неочевидном графе.

Данный способ подходит как для графов, ребра которых не имеют весов, так и напротив — графов, ребра которых имеют жестко заданный вес, взвешенных графов.

Поиск кратчайшего пути в графе через упрощение подразумевает под собой алгоритм, выполнив который можно получить математически подтвержденный кратчайший путь от одной вершины до другой.

Для описания алгоритма мы возьмем простой взвешенный граф, имеющий 8 вершин и 8 ребер, граф имеет разветвления, схождения, несколько идущих подряд ребер, схождение четырех ребер в одной вершине и потенциально ложные пути решения. В целях удобства повествования, поиск пути будет осуществляться от нижней вершины до верхней (в соответствии с ориентацией рисунка в статье). Описанный граф изображен на Рис. 1.

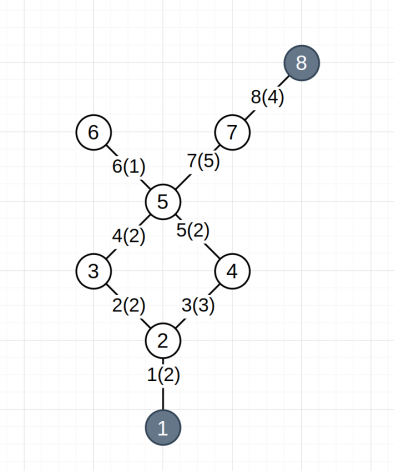
Рис. 1. Граф образец. Напротив каждого ребра указан номер, в скобках указан вес ребра. Внутри вершин указаны их номера. 1 — начальная точка поиска пути, 8 — конечная

Итак, перейдем непосредственно к алгоритму.

1. Убираем очевидные тупиковые/непроходные ребра и вершины, не ведущие к конечной точке. В случаем представленного графа это вершина 6 и прилегающее к ней ребро 6. Результат показан на Рис. 2.

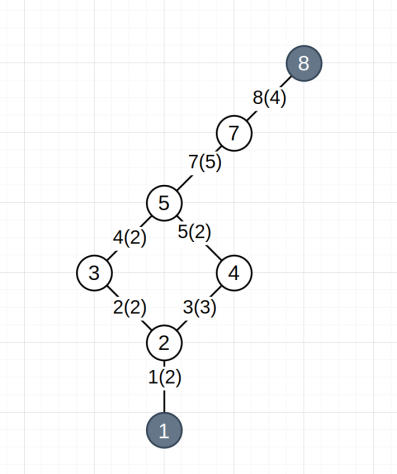
Рис. 2. Результат упрощения графа после первого шага (Убраны непроходные ребра)

2. Все рёбра и вершины, идущие друг за другом и не предполагающие вариативности построения пути, его разветвления или схождения, оптимизируем путем замены нескольких идущих друг за другом ребер одним, имеющим вес , где x — вес ребра, n — количество входящих в цепочку ребер, а i — стартовое ребро. То есть, простыми словами, заменяем идущие друг за другом ребра одним, имеющим вес, равный сумме весов заменяемых ребер. Проведем данную операцию и над нашим графом. Под вышесказанное описание попадают ребра 7 и 8, а также вершина 7. Результат представлен на Рис. 3.

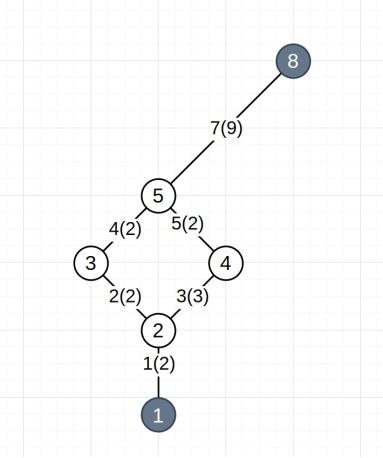
Рис. 3. Результат упрощения графа после второго шага. Ребра 7 и 8, а также вершина 7 заменены одним новым ребром 7, имеющим вес, равный сумме весов замененных ребер. Новое ребро 7 соединяет вершины 5 и 8

3. Находим все потенциальные разветвления пути при прокладывании маршрута от изначальной точки до конечной и проводим дублирование части графа, расположенной со стороны начала маршрута от развилки. Количество дубликатов будет равно количеству ребер, выходящих из точки разветвления.

Нумерацию, а также веса в дубликатах ребер и вершин следует оставить без изменений, сохранив изначальные значения. Все ребра, ранее соединявшиеся с вершиной-перекрестком, теперь необходимо соединить каждый со своим дубликатом ранее идущей части.

Проведем данную операцию с нашим графом. Под данную оптимизацию попадают вершины 1 и 2, а также ребро 1. Результат представлен на Рис. 4.

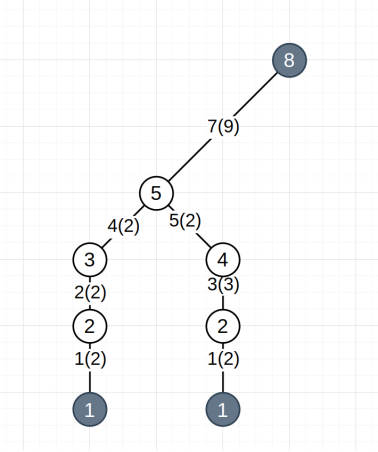
Рис. 4. Результат упрощения графа после третьего шага. Вершины 1 и 2, а также ребро 1 продублированы с сохранением нумерации и весов, ребра 2 и 3, ранее приходившие в одну вершину, теперь соединены каждый со своим дубликатом

4. Проводим операцию, аналогичную операции из 3-го пункта, но в обратной последовательности (от конечной вершины до исходной). То есть, в случае схождения потенциальных путей, мы дублируем вершину-перекресток и все ребра, исходящие из неё в сторону конечной вершины, сохраняя нумерацию и веса ребер и вершин. Конечная вершина не является исключением из правил и так же дублируется. Результат для графа-образца представлен на Рис. 5.

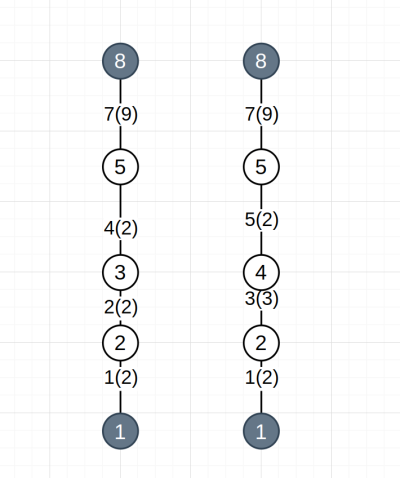
Рис. 5. Результат упрощения графа после четвертого шага оптимизации. Вершины 5 и 8, а также ребро 7 продублированы, нумерация и веса сохранены. Ребра 4 и 5, ранее приходившие в вершину 5, теперь соединены с соответствующим дубликатом

5. На данном этапе мы имеем набор простых графов-путей, не содержащих сочленений, разветвлений и схождений. Необходимо провести оценку графов-путей, выполнив два подэтапа:

1. Пронумеровать каждый граф-путь
2. Обозначить для каждого графа-пути , где x — вес ребра, n — количество ребер в графе-пути, i — стартовое ребро

Проведем данную операцию для нашего примера. Результат на Рис. 6.

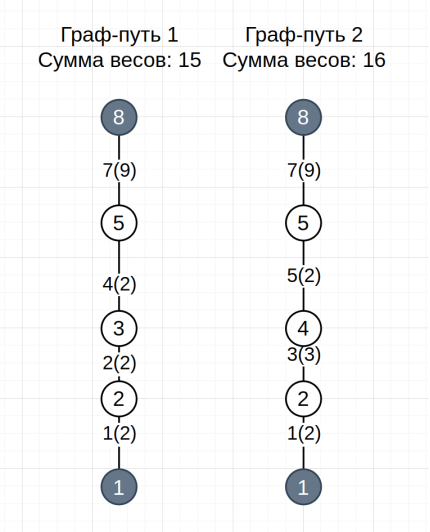
Рис. 6. Результат оценки графов-путей после всех шагов оптимизации. Мы имеем 2 графа-пути с суммарными весами 15 и 16

6. Для выбора кратчайшего пути необходимо сравнить веса всех графов-путей и определить минимальный из доступных. Данный граф-путь будет являться наиболее оптимальным. В нашем случае это Граф-путь 1 с весом 15. В случае наличия равновесных графов-путей, они будут равнозначными в рамках длины пути.

Возьмем множество вершин определенного нами графа-пути:

A = {1, 2, 3, 5, 8}

Данное множество будет являться маршрутом, применим его к нашему изначальному графу. На шаге два мы скрыли вершину 7, но маршрут все равно пройдет через неё, так как другие варианты прохождения данного участка отсутствуют. Результат на Рис. 7.

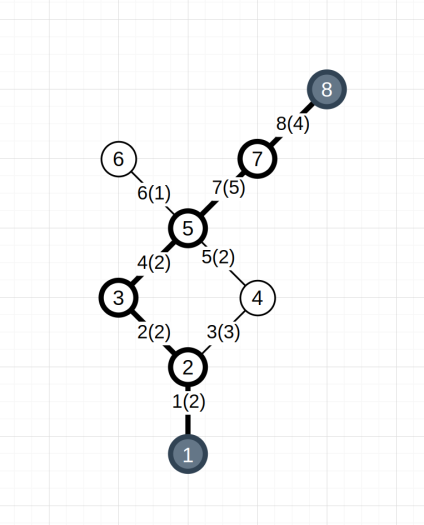
Рис. 7. Точки маршрута множества A, полученные из вершин Графа-пути 1, наложены на изначальный граф-пример, образуют тем самым кратчайший путь прохождения из вершины 1 в вершину 8 (жирными линиями выделены элементы, входящие в путь)

Подведем итог: в результате выполнения представленного алгоритма мы получили методику поиска кратчайшего пути в графе через его упрощение до простейших графов-путей. Алгоритм получился понятным, легким к повторению и подходящим для базового обучения теории графов.

Литература:

1. Задача о кратчайшем пути [Электронный ресурс]: Википедия. Свободная энциклопедия. — URL: https://ru.wikipedia.org/wiki/Задача_о_кратчайшем_пути (дата обращения: 12.01.2025).

2. Галкина В. А. Глава 4. Построение кратчайших путей в ориентированном графе // Дискретная математика. Комбинаторная оптимизация на графах. — Москва: Издательство «Гелиос АРВ», 2003.

3. Ойстин Оре. Теория графов / Под ред. И. М. Овчинниковой. — Издательство наука, 1980.