В данной статье рассматривается разработка метода автоматического поиска начала цифрового сигнала.
Ключевые слова: цифровой сигнал, переходной процесс, сигнал, автоматический поиск начала, образ, полезный сигнал.
Введение
Измерение скорости ультразвука производится при помощи двух пьезоэлектрических преобразователей, один выступает в качестве излучателя и подключается к генератору, второй в качестве приемника и подключается к осциллографу, с него мы и наблюдаем цифровой сигнал, прошедший через какой-либо материал, помещенный между пьезоэлектрическими преобразователями. Само измерение проходит за счет вычисления разницы во времени прохождения сигнала в измерении с материалом и без материала.
В процессе изучения цифровых сигналов была замечена особенность, при прохождении некоторых материалов у сигнала появлялся дополнительный переходной процесс, частота сигнала в котором не совпадает с частотой установившегося сигнала. Откуда появилась гипотеза, что если за отсчетную точку времени для измерения задержки брать точку после этого переходного процесса, то измерение может быть некорректным, так как визуально видно, что четверть периода в начальном переходном процессе не равна четверти периода установившего сигнала, а следовательно, весь сигнал сдвигается на тот самый переходной процесс, поэтому предлагается производить измерения и за отсчетную точку принимать самое начало сигнала. Таким образом, целью работы является разработка метода автоматического поиска начала цифрового сигнала
Цель работы:
Разработка метода автоматического поиска начала цифрового сигнала
Задачи работы:
- Изучение цифрового сигнала
- Математическая обработка сигнала
- Поиск начала сигнала
- Написание программы
Изучение переходного процесса переходного сигнала.
При снятии осциллограмм цифрового сигнала и его анализе была замечена особенность при прохождении сигнала через некоторые материалы. Данная особенность является переходным процессом, который возникает при первом же попадании излучения на материал. При его более подробном изучении были сделаны выводы, что частота сигнала в данном переходном процессе не равна частоте уже устоявшегося сигнала. Иными словами, четверть периода сигнала в начальном переходном процессе не равна четверти периода всего остального сигнала, при одинаковых значениях на генераторе. Таким образом был сделан вывод, что измерения стоит проводит по самому началу сигнала, но для этого необходимо произвести математическую обработку сигнала.
Математическая обработка цифрового сигнала
При принятии цифрового сигнала с осциллографа имеется большое количество шумов, которые затрудняют работу с сигналом. Большое количество шумов не позволяет с высокой точностью и регулярностью определять контрольные точки на сигнале, в данном случае одними из таких точек будут являться локальные экстремумы функций, а также сама точка начала сигнала. Для решения данной проблемы было задействовано несколько методов:
– усреднение при помощи встроенной функции осциллографа
Данная функция не требует никого дополнительного написания кода в программе, так как она встроена в прибор. Функция работает следующим образом: осциллограф снимает заданное количество осцилляций, а далее при помощи своих математических функция находит среднее значение каждой точки на осциллограмме и выдает итоговую. Таким образом сигнал сильно сглаживается и работать с ним становится легче.
– наложение математического фильтра на сигнал
Математический фильтр выбирался по двум критерия:
– скорость работы фильтра
– общее качество фильтрации
Таким образом был сделан вывод, для сигнала необходим не требовательный к математике фильтр, благодаря чему он будет срабатывать быстро и при этом хорошо сглаживающий сигнал. Под эти критерии был подобран фильтр скользящего среднего и наложен на необработанный цифровой сигнал с осциллографа.
Поиск начала сигнала
После получения сигнала с осциллографа возник вопрос о самом методе и поиске начала сигнала. Стало понятно, что для большей информации нужны некоторые контрольные точки на графике, в виде экстремумов.
Поиск экстремумов можно осуществить несколькими способами:
– написать собственную функцию, которая будет определять экстремумы на основе данных первой производной
– воспользоваться готовой функцией библиотеки Scipy под названием find_peaks
Очевидного решения как сделать лучше и качественней не было, поэтому было принято решение воспользоваться обоими методами и сравнить их между собой
В основе логики написания функции лежит знание о первой численной производной, а именно то, что первая производная показывает скорость роста первоначального графика, таким образом мы с точностью сможем определить главные экстремумы первоначального графика. Потому как нули функции первой производной есть ничто иное, как пики и локальные экстремумы первоначальной функции.
Для взятия производной первого порядка был использован метод двусторонней разности [1]. После написания функция работала корректно и отображала нужные при исследовании экстремумы.
Find_peaks это функция встроенная в библиотеку Scipy, которая используется для поиска положительных экстремумов функции. Find_peaks является достаточно удобной и точной, потому как имеет несколько параметров для регулирования поиска экстремумов. Благодаря этим настройкам функция становится достаточно гибкой и удобной в использовании. Для большего понимания гибкости настроек функции следует их перечислить [2]:
– height: высота минимального пика
– distance: расстояние между соседними пиками
– prominence: расстояние от максимума до ближайшего минимума
– width: ширина пиков
Для более точно определения пиков было принято решение использовать из параметров функции только distance и prominence, потому как при исследовании не важна никакая ширина пиков и нет никакой привязки к этому, а если использовать параметр с высотой минимального пика то существует большая вероятность нахождения лишних точек, которые не будут в себе нести никакой полезной информации и первый пик сигнала из-за этого может быть некорректно определен.
После написания обеих функций было произведено сравнение. И сразу стало понятно, что функция find_peaks работает многократно быстрее, чем собственноручно написанная формула, при той же точности результатов. Таким образом был сделан выбор в пользу готовой функции find_peaks. График и отмеченные на нем пики сигнала приведены на рисунке.
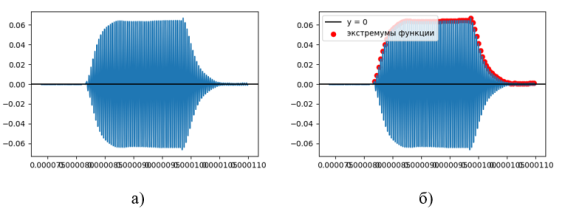
Рис. 1. а) сигнал до отображения пиков б) сигнал после отображения пиков
Помимо экстремумов необходимо также найти нули функции, а точнее один единственный ноль. Так как рассматривать весь график и отображать все точки не нужно, то при написании функции было учтено, что из множества нулей функции нужен только один, находящийся перед первым пиком.
Сама функция нахождения нулей была написана следующим образом. Происходит чтение данных массива значений по вертикальной оси осциллографа, она же показывает значение напряжения. Так как отсчет осциллографа далеко не всегда может совпадать с истинным нулем функции, то происходит поиск наиболее ближнего отсчета осциллографа к значению нуля. Каждый отсчет осциллографа идет проверка на смену знака у массива значений вертикальной оси осциллографа. После нахождения точек максимально приближенных к нулю необходимо найти единственную точку, которая нам нужна. Для этого было написано условие для ее поиска. Поиск осуществлялся при помощи индексов. Имеется весь массив индексов, он приходит с основным сигналом, при помощи find_peaks были найдены пики и несложно среди них выделить первый и его индекс соответственно.
Таким образом при нахождении ближайшего нуля будет использоваться сравнение индекса точки нуля функции с индексом точки первого пика. Это наиболее просто способ, потому как достоверно известно, что у функции имеется пересечение нуля, после которого начинается синусоидальный сигнал и до первого пика повторного пересечения быть не может. Искомая точка для отображения на графике была найдена и представлена на рисунке зеленым цветом.
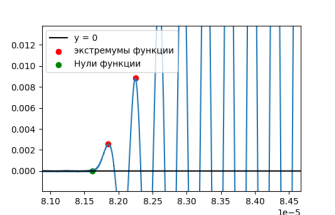
Рис. 2. Искомый ноль функции перед первым пиком
После нахождения первого пика и нужного нуля функции мы получили отрезок, в котором умещается первое возрастание графика полезного сигнала. Именно эту область графика стоит рассматривать для реализации метода. При должном приближении этого отрезка видно, что возрастание происходит неравномерно, и если продолжить середину этого отрезка до прямой нуля координат, то будет видно, что эта точка не совпадает с отмеченной ранее зеленым цветом. В рассмотрении начала сигнала нас интересует именно тока предположительного пересечения, так как эти точки не совпадают как раз из-за переходного процесса. Было принято решение еще ограничить данный отрезок и взять его среднюю часть для дальнейшей обработки.
Была взята точка, которая находится в 130 отсчетах осциллографа от точки нуля. Выбрана она была для того, чтобы рассмотреть ее и последующую точку. Так как в середине отрезка от нуля до первого пика график похож на прямую, то рассмотрим две точки из середины и найдем их угловой коэффициент между собой. После нахождения углового коэффициента между точками аппроксимируем прямую с таким же угловым коэффициентом до точки пересечения с осью x. Таким образом мы нашли искомую точку начала сигнала, она приведена на рисунке
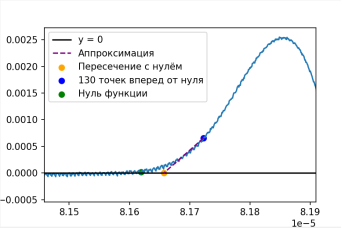
Рис. 3. Искомая точка начала полезного сигнала
Таким образом был разработан метод автоматического поиска начала полезного сигнала. Данный метод включает в себя:
– обработку поступающего цифрового сигнала
– отображение пиков и нулей функции
– выделение точки для проведения аппроксимации
– проведение аппроксимации для поиска начала сигнала
В процессе написания статьи были изучены материалы о математической обработке цифровых сигналов, а также множество документаций к библиотекам Python.
Литература:
- find_peaks. — Текст: электронный // scipy: [сайт]. — URL: https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.find_peaks.html (дата обращения: 26.01.2025).
- Функция скользящей средней для временного ряда. — Текст: электронный // stackoverflow: [сайт]. — URL: https://ru.stackoverflow.com/questions/1565052 (дата обращения: 26.01.2025).
- Как аппроксимировать нелинейную функцию в Python. — Текст: электронный // stackoverflow: [сайт]. — URL: https://ru.stackoverflow.com/questions/808284 (дата обращения: 26.01.2025).
- Нахождение производной на Python. — Текст: электронный // stackoverflow: [сайт]. — URL: https://ru.stackoverflow.com/questions/630116 (дата обращения: 26.01.2025).







