В статье рассматривается численное решение ряда стандартных задач квантовой механики с аналитическими решениями, таких как потенциальная яма, квантовый гармонический осциллятор и атом водорода. Целью работы является численное решение этих задач с использованием библиотек Python и сравнение полученных результатов с известными аналитическими решениями. Работа включает в себя применение методов конечных разностей и конечных элементов для численного решения задач, анализа и сравнения затрачиваемой вычислительной мощности от размерности сетки вычислительного пространства.
Ключевые слова: квантовая яма, гармонический осциллятор, атом водорода, энергетический спектр, волновые функции, уравнение Шредингера, метод конечных разностей, метод конечных элементов.
The article discusses the numerical solution of a number of standard problems of quantum mechanics with analytical solutions, such as the potential well, quantum harmonic oscillator and the hydrogen atom. The aim of the work is to numerically solve these problems using Python libraries and compare the results with known analytical solutions. The work includes the application of finite difference and finite element methods for numerical solution of problems, analysis, and comparison of the computational power expended on the grid dimension of the computational space.
Keywords: quantum well, harmonic oscillator, Israeli atom, energy spectrum, wave functions, Schrödinger equation, finite difference method, finite element method.
Введение
В квантовой механике есть всего несколько задач, которые имеют аналитические решения и достаточно просты для преподавания студентам бакалавриата. Даже если вы продолжите изучать квантовую механику в магистратуре, список все еще, вероятно, будет состоять только из задач: свободной частицы, потенциальной ямы, квантового гармонического осциллятора и атома водорода [5]. В данной работе мы попытаемся решить задачи из приведенного списка численными методами при помощи библиотек Python и проведем сравнение с аналитическими решениями.
Как только мы найдем аналитическое решение, мы попытаемся решить проблему численно, используя численные методы решения — метод конечных разностей и конечных элементов [1,2]. Оба метода имеют различия в подходах к дискретизации и решению уравнений. Метод конечных разностей проще в реализации для задач с регулярной геометрией, но может столкнуться с трудностями при работе со сложными границами или неструктурированными сетками, так как он использует аппроксимацию производных с помощью разностей между значениями функции в узловых точках сетки. Метод конечных элементов, напротив, делит область на элементы и аппроксимирует решение внутри этих элементов с помощью полиномов [1]. Это показывает большую точность при работе сложными задачами. Принципиальная разница заключается не в том, что это один метод, а в принципиально различных подходах к дискретизации: метод конечных разностей с узловыми значениями и разностными производными. Метод конечных элементов разбивает область на элементы с полиномиальной аппроксимацией внутри каждого элемента.
Суть исследования при использовании методов конечных разностей и конечных элементов заключается в эффективной аппроксимации сложных математических моделей более простыми дискретными аналогами с целью минимизации вычислительных затрат и погрешностей численного решения. Для МКР это достигается путём замены непрерывных дифференциальных операторов их дискретными аналогами на регулярной сетке. В случае метода конечных элементов происходит разбиение сложных геометрических областей на совокупность простых подобластей с последующим построением кусочно-полиномиальных аппроксимаций решения на этих элементах. Оба метода требуют тщательного планирования численного эксперимента для достижения баланса между точностью и вычислительными затратами, что позволяет решать широкий спектр задач в различных областях физики и инженерии.
Несмотря на различия, оба метода преследуют единую цель — получить численное решение дифференциальных уравнений, трансформирую их в систему алгебраических уравнений [2]. Однако, возникает вопрос потребляемого вычислительного объёма памяти при использовании данных методов при решении представленных задач. Оптимизация и снижение потребляемого вычислительного объёма памяти может быть связана с применением параллельных вычислений, использованием разреженных матриц, адаптивной дискретизацией с переменным шагом сетки.
Описание исследуемой системы и методов решения
- Атом водорода
Задача атома водорода — один электрон в кулоновском (обратно квадратичном) потенциале [5]. Это стандартная задача, решаемая на вводных курсах квантовой механики. Помимо того, что это одна из немногих проблем с замкнутой формой решения, атом водорода чрезвычайно интересен, потому что он дает нам основные инструменты для понимания того, как работает окружающий нас мир. Он показывает нам, как простой потенциал приводит к квантованным уровням энергии и наконец, объясняет, что такое квантовые числа и откуда они берутся. Становятся очевидными структура и основные особенности периодической таблицы. И отсюда проблемы атома водорода связывают физику и химию и позволяют нам понять подавляющее большинство явлений, происходящих вокруг нас. И если этого недостаточно, проблема водорода имеет большое значение, если смотреть на нее через призму истории физики — она сыграла важную роль в развитии квантовой механики, а ее решение стало первым триумфом теории, которая произвела революцию не только в мире физики.
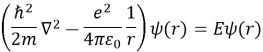
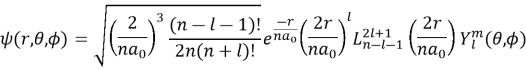
где
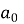
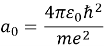
Хотя решение выглядит пугающе, большая часть сложности заключается в члене нормализации и довольно незнакомых сферических гармониках и полиномах Лагерра. Энергия E определяется по формуле:
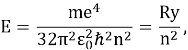
где Ry — один Ридберг, или 13,605 эВ.
Энергетический спектр квантуется и подчиняется обратному квадрату. В этом решении, которое не учитывает магнитные и спиновые эффекты, только главное квантовое число n определяет энергию состояния.
- Квантовая яма
Квантовая яма — это теоретическая модель, описывающая систему частиц, ограниченных потенциалом в одномерном или многомерном пространстве [5]. Основная идея заключается в том, что частицы «заперты» в области с низким потенциалом (в яме), в то время как за ее пределами потенциальная энергия стремится к конечному пределу. Это приводит к дискретным значениям энергии и описывает поведение частиц, таких как электроны в полупроводниках. Эти структуры обладают уникальными электронными и оптическими свойствами, что делает их особенно привлекательными для разработки новых устройств в области электроники и фотоники.
Уравнения Шредингера для квантовой ямы:
Для одномерной квантовой ямы потенциал 𝑉 описывается следующим образом:
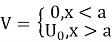
Уравнение Шредингера в одномерном случае выглядит следующим образом:
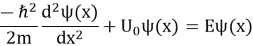
где: ℏ — редуцированная постоянная Планка, 𝑚 — масса частицы, 𝜓(𝑥) — волновая функция, 𝐸 — энергия частицы.
Для случая бесконечно глубокой квантовой ямы,
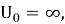
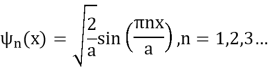
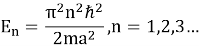
Энергетический спектр квантовой ямы дискретен, обратно пропорционален квадрату ширины квантовой ямы (
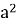
- Гармонический осциллятор
Задача о квантовом гармоническом осцилляторе представляет собой модель, описывающую движение частицы в потенциальной яме, описанной квадратичной функцией [5]. Это один из самых важных примеров в квантовой механике, используемый для изучения колебательных систем, таких как атомы в молекулах, фононы в кристаллической решетке и др.
Изучение квантового гармонического осциллятора имеет критическое значение для понимания множества физических явлений, включая квантовые колебания, спектры излучения и механизмы взаимодействия частиц. Эта модель также служит основой для более сложных систем и подходит для анализа в таких областях, как молекулярная физика, теоретическая химия и квантовая оптика. Работы по исследованию квантового гармонического осциллятора начали активно развиваться с рождения квантовой механики в начале 20 века. Одним из ключевых вкладов стало решение уравнения Шредингера для осциллятора, предложенное Эрвином Шредингером [5]. С тех пор значительное внимание уделялось анализу квантового моделирования колебательных систем, включая эффекты, возникающие при взаимодействии осциллятора с внешними полями.
Для гармонического осциллятора потенциал можно записать как:
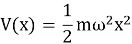
где: 𝑚 — масса частицы, 𝜔 — угловая частота осциллятора.
Уравнение Шредингера в одномерном случае выглядит следующим образом:
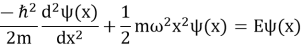
где: ℏ — приведенная постоянная Планка, 𝜓(𝑥) — волновая функция, 𝐸 — энергия системы.
Дискретные значения энергии описываются формулой:
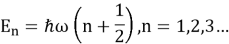
В отличие от классического осциллятора, который может принимать любые значения энергии, квантовый гармонический осциллятор только допускает определённые, квантованные уровни. Наличие добавочного члена ℏω/2 указывает на то, что система обладает нулевой точечной энергией, даже при n=0. Этот аспект иллюстрирует феномен квантового флуктуации энергии, который отличается от классического представления о состоянии покоя.
Волновые функции гармонического осциллятора имеют вид:
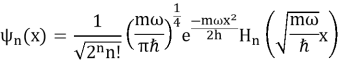
где 𝐻 𝑛 — полиномы Эрмита. Эти волновые функции являются ортогональными и нормированными, что означает, что
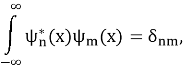
Где
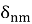
Таким образом, каждая волновая функция представляет собой стоячую волну в потенциальной яме, а ее форма определяется соответствующими полиномами Эрмита.
Поведение волновой функции осциллятора демонстрирует характерные особенности с ростом квантового числа n. Для малых значений n волновые функции имеют относительно простую, симметричную структуру, однако с увеличением n наблюдается нарастание количества узловых точек и изменение формы функций, что указывает на проявление более сложных квантовых состояний. Это изменение отражает природу вероятностного распределения частиц в пространстве, которое становится более распределённым и менее локализованным по мере увеличения энергии.
Результаты и обсуждения
В представленном исследовании рассматриваются результаты численного решения квантово-механических задач с использованием двух различных методов: метода конечных разностей (МКР) и метода конечных элементов (МКЭ). Программная реализация данных методов осуществляется на языке Python с применением встроенных библиотек, таких как NumPy, SciPy, matplotlib и Plotly, что позволяет эффективно производить необходимые вычисления и визуализацию решений.
Для анализа эффективности работы обоих методов было проведено исследование, заключающееся в определении объёма использованной памяти в зависимости от размерности сетки вычислительного пространства. Результаты показывают, что метод конечных разностей демонстрирует определённые преимущества в простоте реализации и скорости вычислений, однако его применение ограничивается лишь относительно простыми геометриями и условиями на границах. Наоборот, метод конечных элементов, несмотря на большую вычислительную сложность, способен успешно обрабатывать более сложные геометрические задачи и предлагать большую гибкость в выборе параметров вычислительной сетки.
1. Численное решение атома водорода
При помощи методов МКР и МКЭ определили спектр энергий и плотности распределения волновых функций атома водорода. Помимо этого провели анализ влияния размерности сетки пространства на величину затрачиваемой вычислительной мощности.
Далее на рисунке 1 представлены результата решения: три волновые функции для различных энергетических состояний атома водорода. Синяя кривая (E = -3.40 эВ) это состояние с наибольшей энергией связи, характеризующееся одной ярко выраженной амплитудой около 2.5 Å и быстрым затуханием к 5 Å, что указывает на сильную локализацию атома. Зеленая кривая (E = -1.51 эВ) отображает промежуточное состояние с двумя максимумами, меньшим около 1 Å и более выраженным около 7.5 Å, с узловой точкой около 4 Å. Красная кривая (E = -0.83 эВ) показывает состояние с наименьшей энергией связи, имеющее три максимума и две узловые точки, распространяясь до 17.5 Å. Эти функции формируют характерное распределение функции плотности вероятности, где каждое последующее состояние обладает меньшей энергией связи и большим числом узлов, что согласуется с квантово-механическим описанием атома водорода.
При увеличении главного квантового числа n, наблюдается усложнение волновой функции: количество узлов увеличивается, и пространственное распределение электрона расширяется. Орбитальное квантовое число l определяет угловую часть волновой функции и симметрию распределения плотности вероятности, в то время как магнитное квантовое число m влияет на ориентацию орбитали.
Рис. 1. Волновая функция атома водорода по оси x
На рисунке 2 показана визуализация плотности распределения волновых функций атома водорода в плоскости x-y. Для каждого последующего случая решения изменяется квантовые числа: n, l, m. По мере изменения квантовых чисел происходит перераспределение плотности и волновых функций, усложнение формы атомных обителей и увеличение количества узлов. Например, p-орбиталь (l=1) в возбужденном состоянии (n=2). Плотность волновой функции наиболее высока в центре каждой доли и уменьшается радиально. Между петлями есть узловая плоскость (где вероятность равна нулю), проходящая через ядро. Далее, в таблице 1 приведено сравнение размерности сетки пространства на величину затрачиваемой вычислительной мощности для двух численных методов МКР и МКЭ.
Таблица 1
Расчет методами МКР и МКЭ атома водорода, влияние размерности сетки на затрачиваемую память
|
Разрешение |
Размерность сетки |
Количество памяти (Мбайт) МКР/МКЭ |
|||
|
n=1; l = 0 |
n=2; l = 0 |
n=2; l = 1 |
n = 3, l = 1 |
||
|
100 |
10000 |
0,76/2,34 |
0,76/2,34 |
0,76/2,34 |
0,76/2,34 |
|
200 |
40000 |
3,05/9,41 |
3,05/9,41 |
3,05/9,41 |
3,05/9,41 |
|
400 |
160000 |
12,21/37,73 |
12,21/37,73 |
12,21/37,73 |
12,21/37,73 |
|
680 |
462400 |
35,28/109,18 |
35,28/109,18 |
35,28/109,18 |
35,28/109,18 |
|
1000 |
1000000 |
76,29/23624 |
76,29/236,24 |
76,29/236,24 |
76,29/236,24 |
|
1500 |
2250000 |
171,66/531,74 |
171,66/531,74 |
171,66/531,74 |
171,66/531,74 |
|
2000 |
4000000 |
30518/945,5 |
305,18/945,5 |
305,18/945,5 |
305,18/945,5 |
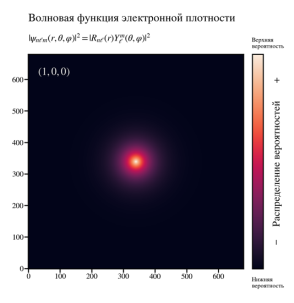
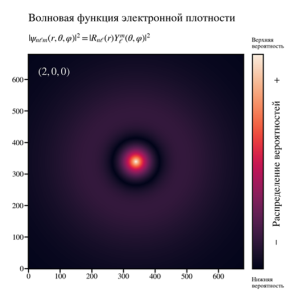
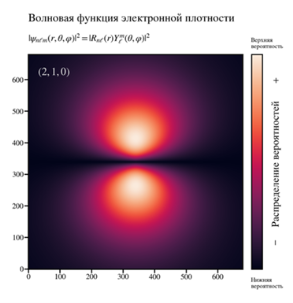
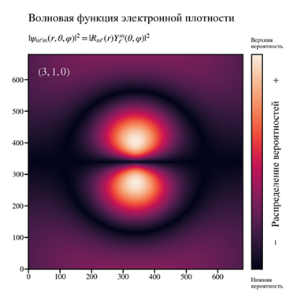
Рис.2. Плотность распределения волновой функция атом водорода а) n=1; l = 0; m =0; б) n=2; l = 0; m =0; в) n=2; l = 1; г) n = 3, l = 1, m = 0
Анализ данных таблицы 2 показывает явную взаимосвязь между размерностью сетки и объемом используемой памяти при моделировании атома водорода методом конечных разностей. Наблюдается нелинейный рост потребления памяти с увеличением разрешения сетки, причем эта зависимость не всегда монотонна. Таким образом, выбор оптимальной размерности сетки играет критическую роль в обеспечении точности расчетов при одновременной оптимизации использования вычислительных ресурсов.
2. Численное решение задачи «квантовая яма»
Далее, двумя численными методами конечных определили спектр энергий и распределение волновых функций в квантовой яме. С увеличением уровня энергии количество узлов в каждой волновой функции также увеличивается, что соответствует принципам квантовой механики для связанных состояний в конечной потенциальной яме. Результаты численного моделирования квантовой ямы позволяют наглядно продемонстрировать ключевые квантово-механические эффекты, характерные для данной системы. Визуализация волновых функций демонстрирует их характерную структуру в виде стоячих волн, рисунок 3. Примечательно, что с увеличением квантового числа n наблюдается закономерное увеличение числа узлов волновой функции. На рисунке 4 показана визуализация плотности распределения волновых функций для квантовой ямы в плоскости x-y.
Далее, в таблице 2 приведено сравнение размерности пространства сетки на затрачиваемую вычислительную мощность задачи при решении численными методами МКР и МКЭ.
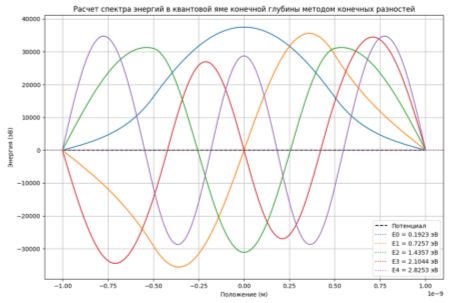
Рис. 3. Расчет спектра энергий в квантовой яме конечной глубины методом конечных разностей, визуализация энергетического спектра и волновых функций системы
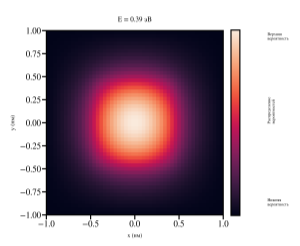
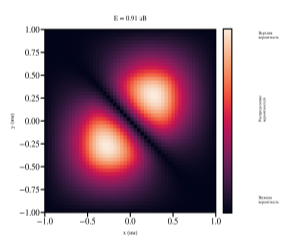
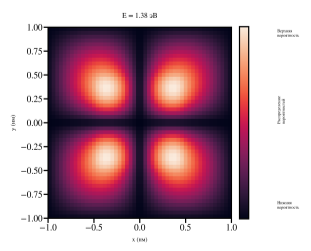
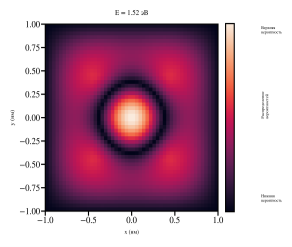
Рис. 4. Плотность распределения волновых функций для квантовой ямы с 1 по 4-ю подзону
Таблица 2
Расчет методами МКР и МКЭ квантовая яма, влияние размерности сетки на затрачиваемую память
|
Разрешение |
Точки сетки |
Количество памяти (Мбайт) МКР/МКЭ |
|||
|
15 нм. |
25 нм. |
50 нм. |
100 нм. |
||
|
100 |
10000 |
34,34/71,12 |
95,39/127,42 |
381,51/423,17 |
525,96/712,11 |
|
200 |
40000 |
61,65/137,35 |
126,45/281,51 |
236,7/525,96 |
361,3/803,67 |
|
400 |
160000 |
247,05/549,36 |
371,25/825,96 |
496,3/1103,67 |
1986,3/4414,37 |
|
680 |
462400 |
400/887,60 |
904,5/2009,92 |
5446,3/12639,42 |
7386,3/16557,16 |
|
1000 |
1000000 |
649,3/1433,34 |
2266,2/5036,93 |
10416,1/23147,35 |
14664,6/32588,65 |
|
1500 |
2250000 |
1675,8/3724,93 |
5605,6/12457,96 |
17473,4/38831,26 |
19524,6/43323,90 |
|
2000 |
4000000 |
2579,8/5733,14 |
7716/17147,35 |
23564,3/51588,65 |
27608,4/61353,09 |
Результаты демонстрируют взаимосвязь между размерностью сетки и потреблением вычислительной памяти. Ключевые наблюдения показывают нелинейный характер роста памяти при увеличении разрешения сетки. В диапазоне от 100 до 400 точек наблюдается незначительные флуктуации объёма используемой памяти для различных квантовых состояний. Скачок памяти происходит при переходе от 680 к 1000 точкам, этот эффект демонстрирует, что увеличение точности расчетов не всегда линейно коррелирует с ростом вычислительных ресурсов.
3. Численное решение Гармонический осциллятор
Далее, численными методами определили спектр энергии и распределение волновых функций для задачи гармонического осциллятора. На рисунке 5 приведены результаты расчетов уровней энергии и распределения волновых функций, в гармоническом осцилляторе. Результаты для гармонического осциллятора демонстрируют волновые функции первых пяти энергетических состояний. Энергетический спектр показывает равномерное увеличение энергии между последовательными уровнями с шагом E = 0.165 эВ. Основное состояние (n = 0) имеет гауссову форму без узлов, в то время как каждое последующее состояние демонстрирует n узлов. Четные состояния (n = 0, 2, 4) обладают симметрией относительно начала координат, тогда как нечетные состояния (n = 1,3) показывают асимметрию. Численные результаты согласуются с аналитическими решениями для квантового гармонического осциллятора.
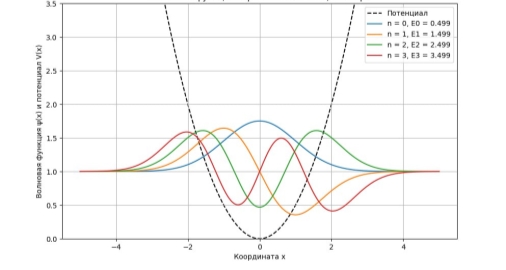
Рис. 5. Положение уровней энергии и распределение волновых функций для квантового гармонического осциллятора
Далее, в таблице 3 приведены результаты расчетов для задачи квантового гармонического осциллятора. Проведено сравнение двух методов по затрачиваемой вычислительной мощности от размерности сетки пространства.
Таблица 3
Расчет МКР и МКЭ задачи гармонического осциллятора, влияние размерности сетки на вычислительную мощность
|
Разрешение |
Точки сетки |
Количество памяти (Мбайт) МКР/МКЭ |
|||
|
Случай 1 |
Случай 2 |
Случай 3 |
Случай 4 |
||
|
100 |
10000 |
0,45/0,99 |
0,47/1,02 |
0,57/1,05 |
0,68/1,11 |
|
200 |
40000 |
1,61/3,57 |
1,84/3,62 |
1,87/3,67 |
1,92/3,78 |
|
400 |
160000 |
4,89/10,85 |
4,93/10,96 |
4,97/11,12 |
4,99/11,18 |
|
680 |
462400 |
14,19/31,5 |
14,21/31,87 |
14,25/32,43 |
14,32/33,05 |
|
1000 |
1000000 |
30,53/67,77 |
30,58/68,12 |
30,83/68,24 |
31,24/69,07 |
|
1500 |
2250000 |
68,67/152,44 |
68,89/153,03 |
69,21/153,37 |
69,87/153,88 |
|
2000 |
4000000 |
122,08/270,07 |
123,23/271,05 |
124,57/271,89 |
126,24/273,13 |
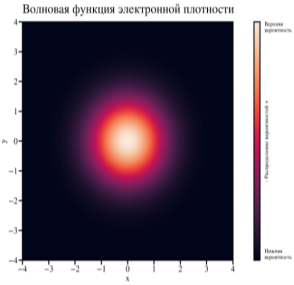
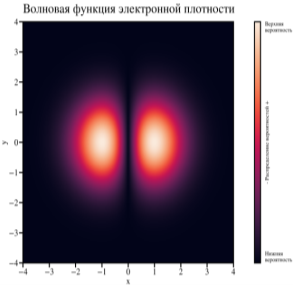
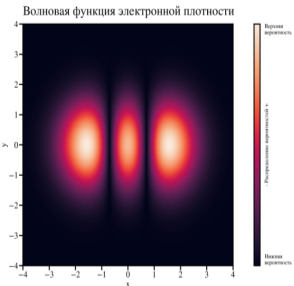
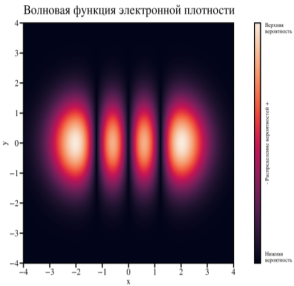
Рис. 6. Визуализация плотности распределения волновых функций с 1 по 4 подзону для квантового гармонического осциллятора
Анализ результатов моделирования атома водорода методами конечных разностей и конечных элементов выявляет сложную взаимосвязь между размерностью сетки и объёмом памяти. При увеличении разрешения сетки наблюдается нелинейный рост потребления вычислительных ресурсов, который не всегда имеет монотонный характер. В диапазоне от 100 до 400 точек заметны небольшие колебания в объёме используемой памяти для различных квантовых состояний. Начиная с 680 точек, потребление памяти стабилизируется, и становятся практически идентичным для всех исследованных конфигураций параметров системы. Явно наблюдается нелинейная зависимость используемого объёма памяти от величины размерности сетки пространства.
4. Обсуждение результатов работы МКР и МКЭ
В данном разделе мы проведем сравнительный анализ зависимости объема затрачиваемой памяти от размерности пространства для трех различных задач с использованием двух методов решения: метода конечных элементов (МКЭ) и метода конечных разностей (МКР). На основании собранных данных построили графики, представленные на Рисунке 8, где отображена величина используемой памяти в зависимости от размерности сетки для решения квантово-механических задач.
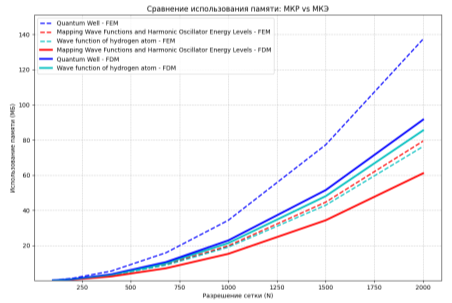
Рис. 7. Графики вычислительной мощности затрачиваемой на решение квантово-механических задач от размерности сетки
По результатам проведённого анализа, сравнили два численных метода — метод конечных разностей и метод конечных элементов, применили их для решения квантово-механических задач. Ключевым показателем эффективности работы метода выявили вычислительную мощность в зависимости от размерности сетки пространства, затрачиваемую на решение конкретной задачи. Результаты исследования показывают, что при увеличении размерности пространства объем памяти, требуемый для метода конечных элементов, значительно возрастает. Например, для решения задачи квантовой ямы 25 нм, при размерности сетки 100x100 объем памяти составляет 127,5 МБ, тогда как при размерности 1000x1000 увеличивается до 5,05 ГБ, аналогичная ситуация и для остальных задач. В то же время, метод конечных разностей для решения квантово-механических задач демонстрирует более стабильное поведение: при тех же размерностях квантовой ямы и сетки он требует 96 МБ и 2,26 ГБ соответственно.
Таким образом, можно сделать вывод, что метод МКЭ, будучи более гибким и точным в решении определенных задач, требует значительно больших ресурсов при увеличении размерности пространства по сравнению с методом МКР. Это подчеркивает важность выбора подходящего численного метода в зависимости от конкретной задачи и доступных вычислительных ресурсов.
Заключение
В заключении настоящей статьи, представлено численное решение стандартных задач квантовой механики, включая потенциальную яму, квантовый гармонический осциллятор и атом водорода, с использованием методов конечных разностей и конечных элементов. Основное внимание было уделено сравнению вычислительной мощности, затрачиваемой на решение этих задач в зависимости от размерности сетки вычислительного пространства.
Результаты показали, что объем памяти, необходимый для метода конечных элементов, значительно увеличивается с ростом размерности сетки. Для задачи квантовой ямы с шириной 25 нм объем памяти при размерности сетки 100x100 составляет 127 МБ, тогда как при размерности 1000x1000 он возрастает до 5,05 ГБ. В то же время метод конечных разностей демонстрирует более устойчивую зависимость: объем памяти при тех же размерностях составляет 96 МБ и 2,26 ГБ соответственно. Таким образом, выводы исследования подчеркивают, что хотя метод конечных элементов предоставляет более высокую точность для определенных типов задач, он требует значительно больших вычислительных ресурсов по сравнению с методом конечных разностей. Это подтверждает важность выбора оптимального численного метода в зависимости от специфики задачи и доступных вычислительных ресурсов.
Литература:
- Эварт Т. Е., Поздяев В. В. Численные методы решения дифференциальных и матричных уравнений. — 2014.
- Mushtaq A., Noreen A., Olaussen K. Numerical solutions of quantum mechanical eigenvalue problems //Frontiers in Physics. — 2020. — Т. 8. — С. 390.
- Титов А. Н., Тазиева Р. Ф. Решение задач линейной алгебры и прикладной математики в Python. Работа с библиотекой SciPy //Казань: Изд-во КНИТУ. — 2023.
- Srnec M. N., Upadhyay S., Madura J. D. A Python Program for Solving Schrödinger’s Equation in Undergraduate Physical Chemistry. — 2017.
- Ландау Л. Д. Лифшиц ЕМ Квантовая механика //Нерелятивистская теория. — 1963.
- Halpern A. M., Ge Y., Glendening E. D. Visualizing Solutions of the One-Dimensional Schrödinger Equation Using a Finite Difference Method. — 2022.







