Рассматривается проблема нагрева волноводов при передаче по ним сигналов повышенной мощности. Предложена расчетная модель нагрева тонкостенной конструкции прямого участка волновода и дифференциальное уравнение его теплового баланса с граничными условиями.
Ключевые слова: космический аппарат, антенно-фидерная система, волновод, сверхвысокочастотный сигнал, потери мощности, скин-слой, нагрев.
Введение. Волноводы относятся к направляющим системам и широко применяются для передачи высокочастотной энергии в радиоэлектронной аппаратуре. В космических аппаратах волноводы являются частью антенно-фидерной системы (АФС) и служат для передачи электромагнитных сигналов сверхвысокой частоты между антеннами и блоками связи.
На различных этапах жизненного цикла, волноводы подвергаются различным внешним силовым, деформационным и температурным воздействиям, носящих как статический, так и динамический характер. Условия статической и динамической прочности волноводов космических аппаратов (КА) связи, а также методика их расчета на все перечисленные внешние воздействия изложены в [1,2].
Возросшие в последнее время требования к функционально-эксплуатационным параметрам космических аппаратов в целом, и их системам связи в частности, привело к необходимости увеличения мощности передаваемого сигнала по антенно-фидерным системам. Наземные испытания волноводно-распределительных систем (ВРС), проведенные в ОАО «Информационные спутниковые системы» им. М. Ф. Решетнева» показали, что при передаче по ним сигналов высокой мощности (порядка нескольких киловатт) происходит существенный нагрев стенок волноводов, которым нельзя пренебречь при расчетах температурных полей и напряжений.
Обзор литературы [3–7] по данной проблеме показал, что все авторы рассмотренных источников только лишь отмечают очень малые потери передаваемых сигналов в волноводах по сравнению с другими типами направляющих систем и как следствие делается вывод об отсутствии необходимости учета выделения тепла. Такая ситуация является допустимой при передаче сигналов относительно небольшой мощности. В настоящее же время большая мощность передаваемого сигнала привела к повышению потерь в волноводе с последующим его нагревом, которым нельзя пренебрегать, что требует доработки методов температурного и прочностного расчетов его тонкостенной конструкции, изложенных в [1,2].
Ситуация усугубляется тем, что возможности для рассеивания избыточного тепла в условиях открытого космоса весьма ограничены, особенно при негерметичном исполнении космического аппарата, когда все его элементы и системы подвергаются воздействию солнечного излучения, а конвективный обмен практически отсутствует. Все это затрудняет эффективный отвод тепла и требует выполнения тепловых расчетов с учетом всех факторов, включая и нагрев при передаче сигналов по волноводам.
Потери мощности.
Анализ литературных источников [3–7] показал, что в процессе распространения электромагнитной волны по волноводу происходит затухание передаваемого сигнала вследствие рассеивания части его энергии по тонкостенной конструкции. Причин затухания сигнала несколько:
1) потери в электропроводящем слое материала на внутренних стенках волновода;
2) потери в диэлектрике во внутренней полости волновода;
3) потери на излучение из-за неплотного соединения отдельных элементов участка волноводно-распределительной системы и др.
В большинстве встречающихся на практике случаев, преобладающими являются потери в тонком электропроводящем слое на внутренних стенках волновода [3,4].
В волноводе с идеально проводящим материалом электрические силовые линии строго перпендикулярны к стенкам волновода. В реальных волноводах, вследствие наличия сопротивления материала его внутренних стенок, вектор напряженности электрического поля будет наклонен в сторону распространения сигнала, в результате чего у него появляется некоторая малая тангенциальная составляющая [4].
Такое изменение структуры электрических силовых линий неизбежно приводит к изменению и магнитного поля — у внутренних стенок волновода появляется небольшая нормальная составляющая вектора напряженности магнитного поля, которая принимается равной нулю в случае идеального волновода.
Вследствие возникновения такого поверхностного скин-эффекта, токи проходят не по поверхности стенок волновода, а проникают в них на некоторую небольшую глубину скин-слоя δ и, за счет удельного сопротивления материала, преобразуются в тепло, приводя к затуханию сигнала на выходе (рис.1).
При этом в случае малой мощности передаваемого сигнала, потери мощности относительно невелики и их влиянием на функционально-эксплуатационные и прочностные параметры волновода пренебрегают.
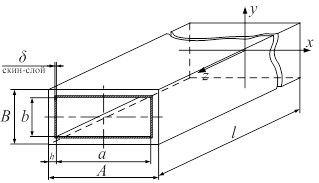
Рис. 1. Прямой элемент волновода
Как известно [3,4], любая составляющая электромагнитного поля вдоль линии волновода (ось z на рис.1) изменяется по экспоненциальному закону. Поэтому изменение (уменьшение) потока энергии вдоль волновода можно охарактеризовать изменением мощности 
передаваемого сигнала по формуле:
[Вт], (1)
где 
— мощность на входе волновода, Вт;
— мощность на выходе волновода, Вт;
α — коэффициент затухания, Дб/м;
l — длина волновода, м.
Согласно выражению (1), потери мощности сигнала в волноводе можно определить с помощью коэффициента затухания α, которым и принято характеризовать степень рассеяния электромагнитной энергии при распространении ее вдоль волновода единичной длины с учетом всех возможных причины этого явления.
Коэффициент потерь.
С помощью некоторых дополнительных упрощений различными авторами [3–7] получены сходные выражения, позволяющие определять величину коэффициента затухания α для различных условий работы волновода. Все эти выражения весьма громоздки и зависят от сочетания многих факторов: вида и размеров волновода, характеристик передаваемой по нему электромагнитной волны, свойств материала стенок волновода, наличия диэлектрика и др.
Например, в наиболее распространенном случае передачи по волноводу прямоугольного поперечного сечения электромагнитной волны типа Н10 коэффициент затухания α, согласно [3], можно определить по следующей формуле:
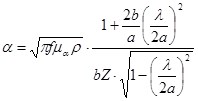[Дб/м], (2)
где π — 3,1415…;
f — частота передаваемого сигнала, кГц;
μa — абсолютная магнитная проницаемость среды, Гн/м;
ρ — удельное сопротивление слоя материала внутренних стенок волновода, в котором наводится ток, Ом*мм2/м;
a — ширина (а>b) внутренней полости волновода, см;
b — высота (а>b) внутренней полости волновода, см;
l — длина волны передаваемого сигнала, см;
Z — волновое сопротивление среды распространения сигнала, Ом.
По полученному выражению (2) построены универсальные диаграммы для определения коэффициентов затухания при различных сочетаниях исходных данных. Например, на рис.2 приведена диаграмма из [3] для определения коэффициента затухания в прямоугольном медном волноводе, заполненном диэлектриком без потерь.
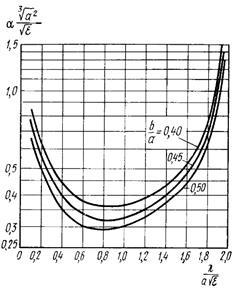
Рис. 2. Диаграмма для определения коэффициента затухания в прямоугольном волноводе [3]
При этом, как указывают авторы [3,4], действительные значения коэффициента затухания будут больше расчетных (2) на 10¸30 % вследствие неучтенных потерь: не плотности соединений, переходное сопротивление, лаковые покрытия и др.
Модель нагрева волновода. Процесс нагрева волновода можно разбить на 2 этапа:
Этап I: Джоулево тепло. Источником нагрева волновода является тонкий скин-слой (рис.1) на его внутренних стенках, который во много раз меньше толщины этих стенок. Толщину скин-слоя 
[мм] можно определить по формуле [1]:
, (3)
где ρ — удельное сопротивление материала волновода, Ом*мм2/м;
f — частота передаваемого сигнала, кГц;
μ — относительная магнитная проницаемость среды.
Для большинства применяемых для волноводов материалов толщины скин-слоя весьма малы, имеют близкие значения и несущественно изменяются (рис.3) во всем СВЧ-диапазоне (3–30 ГГц).
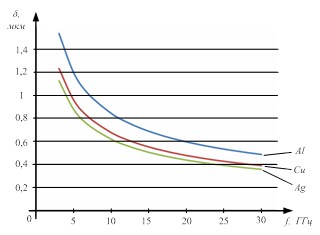
Рис. 3. Значение толщины скин-слоя в зависимости от материала и частоты СВЧ-сигнала
В течение малого промежутка времени будет происходить интенсивный нагрев тонкого скин-слоя за счет протекания в нем наведенных токов от передаваемого сигнала. При этом будем считать что все изменение мощности ΔР передаваемого по волноводу сигнала будет преобразовываться в тепловую энергию. Данный процесс можно считать адиабатическим и его расчет можно проводить на основании закона Джоуля-Ленца [8], согласно которому:
, (4)
или с учетом (6)
, (5)
в итоге
, (6)
где T — температура нагрева;
t — время нагрева;
С — удельная теплоемкость;
М — масса тела, в котором выделяется мощность 
.
Уравнение (6) получено для случая подводимой мощности , произвольно изменяющейся во времени t, что соответствует переменному сигналу. Если подводимую мощность усреднить и принять постоянной во времени (эффективная мощность Рэфф.), то выражение (6) примет вид:
, (7)
где 
и 
— конечные изменения температуры и времени.
Полученные выражения (6) и (7) определяют линейную зависимость нагрева скин-слоя от времени и подводимой мощности.
Этап II: Уравнение теплопроводности. По мере прогрева стенок волновода, на его температурное поле начнет влиять теплообмен с окружающей средой, поэтому этот процесс уже нельзя считать адиабатическим.
Разность температуры внутренних и наружных стенок приведет к возникновению теплового потока по всей толщине стенки волновода [8]:
, (8)
где 
— единичный вектор нормали к поверхности S в сторону увеличения температуры;
— количество тепла, проходящего в единицу времени;
S — площадь изотермической поверхности, м2.
Знак «минус» означает, что вектор плотности теплового потока направлен в сторону уменьшения температуры и противоположно вектору нормали .
Плотность теплового потока также можно определить, согласно основному закону теплопроводности Фурье, по формуле:
, (9)
где l — коэффициент теплопроводности, 
;
— градиент температуры в направлении нормали .
Будем считать, что при передаче электромагнитного сигнала по волноводу происходит равномерный разогрев всех его внутренних поверхностей стенок, которые в результате будут представлять изотермическую поверхность S (рис.3):
S = 2l (a + b). (10)
Направление нормали к изотермической поверхности будет перпендикулярно к каждой из стенок волновода(рис.3). Следовательно, распространение тепла будет происходить только в одном направлении — по нормали в сторону наружных стенок (рис.4).
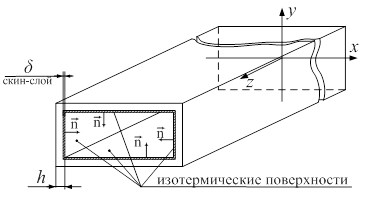
Рис. 4. Направление нормалей к изотермическим поверхностям элемента волновода
Такое заключение позволяет принять для расчета температурного поля волновода одномерную модель распространения тепла вдоль его стенки (рис.5).
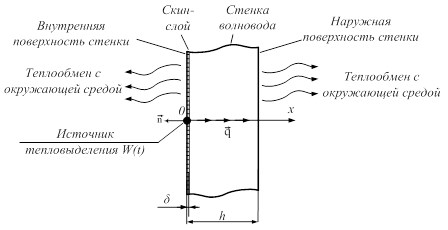
Рис. 5. Расчетная схема нагрева элемента стенки волновода
Выделение тепла ΔQ в скин-слое, при прохождении по нему электромагнитного сигнала, в теории теплопроводности можно смоделировать источником тепла интенсивностью W(t), в результате действия которого температура внутренних стенок повысится. Тогда уравнение теплопроводности с источником тепла будет иметь вид [8]:
, (11)
где 
— коэффициент теплопроводности материала скин-слоя, ;
— плотность материала скин-слоя, 
;
— интенсивность источника тепла в скин-слое,
[Вт/м3];
а — коэффициент температуропроводности материала стенок волновода, определяется по формуле:
в которой
— коэффициент теплопроводности материала стенок, ;
— удельная теплоемкость материала стенок, 
;
— плотность материала стенок, ;
Начальным условием примем однородное температурное поле, которое для одномерной модели запишется как равенство температуры некоторой заданной величине в точках с любой координатой х в начальный момент времени t=0:
. (12)
Граничные условия задаются на границах рассматриваемой области тела, в рассматриваемом случае ими будут являться внутренняя и наружная поверхности стенки волновода (рис.4), на которых будет происходить конвективный теплообмен с окружающей средой, имеющей температуру 
.
Для внутренней поверхности стенки 
граничным условием будет являться теплообмен (конвекцией и лучистым излучением) с окружающей средой, что можно записать как:
,(13)
Второе граничное условие определяет условия теплообмена (конвекция и лучистое излучение) наружных стенок волновода 
с окружающей средой:
. (14)
Граничные условия (13, 14) будут соответствовать работе волновода в среде газа (воздуха), то есть на Земле. Условия эксплуатации волноводов в составе космического аппарата связи, имеющего открытую платформу, предполагают, что они будут функционировать на орбите в среде вакуума, в котором какая-либо конвекция отсутствует, а преобладающим способом переноса и рассеивания энергии (тепла) с волноводов будет являться лучистый теплообмен. В этом случае вместо условий конвекции (13,14) на поверхности стенок волновода необходимо задать условие лучистого теплообмена, согласно закона Стефана-Больцмана, которое имеет вид заданного теплового потока:
,(15)
где 
— приведенный коэффициент лучеиспускания [ккал/м2час0С];
— температура наружной поверхности стенки волновода, от которой передается лучистая энергия;
– температура поверхности, которая воспринимает лучистую энергию.
Полученное дифференциальное уравнение задачи (11) с заданными граничными и начальным условиями довольно просто можно решить как известными аналитическими методами (метод разделения переменных, метод источников и др.), так и численными (метод конечных разностей, метод конечных элементов и др.).
Решение задачи (11–15) позволяет определить стационарное температурное поле прямолинейного участка волновода для любых встречающихся на практике его размеров, у которых известен коэффициент затухания α. Тепловой расчет волноводов с криволинейной продольной осью затруднен, прежде всего, сложностью выбора значений коэффициентов затухания α, поскольку для этих случаев его значения в известной литературе [4–7] не приводятся.
Результаты расчета.
Согласно разработанной модели и полученным уравнениям (11–15) проведены предварительные расчеты температурного поля для прямых участков волноводов с различным типоразмером поперечного сечения (5,5х11, 9х18, 35х15, 25х58 мм) и толщиной стенки (0,6–1,2 мм). Решение выполнялось аналитически методом разделения переменных и численным методом конечных элементов в ППП Ansys. Изучалось время нагрева скин-слоя и установления стационарного температурного поля стенок волновода в двух вариантах: при наличии конвекции (работа волновода в атмосфере Земли), и без нее (работа волновода в вакууме).
Результаты расчетов показывают, что из-за малой толщины скин-слоя (0,5–1,5 мкм), время его нагрева при постоянной подводимой мощности очень мало, поэтому первым этапом адиабатического нагрева скин-слоя волновода можно пренебречь.
Время установления второго этапа нагрева волновода, при котором образуется стационарное температурное поле, определяемое уравнением (11) с ГУ (13–15), вследствие малой толщины стенки (0,6–1 мм) волновода, высокой теплопроводности и низкой удельной теплоемкости их материала (алюминий) составляет несколько секунд. Это означает, что даже при кратковременных сигналах высокой мощности может происходить ощутимый нагрев волноводов.
Заключение
Разработана математическая модель нагрева волновода и получено разрешающее дифференциальное уравнение задачи с начальными и граничными условиями, соответствующие условиям работы ВРС на Земле и в открытом космосе.
Предварительные расчеты показали, что скорость нагрева стенок и волновода в целом весьма высокая, что даже при кратковременном сигнале приводит к повышению его температуры. В условиях космоса, из-за отсутствия конвекции, эффективный отвод тепла будет происходить прежде всего за счет теплопроводности материала через фланцы крепления волновода к блокам АФС, а также между промежуточными опорами и сотопанелями.
Выделение дополнительного тепла при передаче сигналов большой мощности требует уточнения методов теплового расчета волноводов и учета его влияния на условия статической и динамической прочности.
Литература:
1. Сильченко П. Н. Методика расчёта напряжённо-деформационного состояния волноводно-распределительных систем космических аппаратов/ П. Н. Сильченко, И. В. Кудрявцев, М. М. Михнёв, В. Н. Наговицин // Журнал Сибирского федерального университета. Серия: Техника и технологии. 2012 г. № 2. С 150–161.
2. Сильченко П. Н. Анализ динамического состояния волноводно-распределительных систем от воздействия вибрационных нагрузок на этапе вывода космического аппарата на орбиту/ П. Н. Сильченко, И. В. Кудрявцев, М. М. Михнёв, В. И. Халиманович, В. Н. Наговицин // Журнал Сибирского федерального университета. Серия: Техника и технологии. 2012 г. № 2. С. 205–219.
3. Ефимов И. Е. Волновые линии передачи. — М.: Связь, 1979–232с.
4. Воскресенский Д. И. и др. Устройства СВЧ и антенны. 2006. — 378 с.
5. Левин Л. Теория волноводов — М.: Радио и связь. 1981г. — 312с.
6. Кинг Р. Передающие линии, антенны, волноводы. 2012г. — 360с.
7. Котельников И. А. О затухании в волноводе // Журнал технической физики, 2004, т.74. вып.9, С.91–96.
8. Карташов Э. М. Аналитическая теория теплопроводности и прикладной термоупругости. 2012г. — 656с.
