В данной статье рассматриваются интеграционные связи тригонометрии как средство решения проблемы повышения уровня мотивации к учебной деятельности обучающихся. Особое внимание в статье уделено примерам интеграционных связей тригонометрии: с астрономией, с измерениями на поверхности Земли, с физикой, с биологией, с медициной, а также с различными областями человеческой деятельности. Знакомство обучающихся с многообразием применения тригонометрии будет способствовать не только повышению уровня мотивации обучающихся к учебной деятельности, но и поможет сделать им более обдуманный шаг в сторону выбора своей будущей профессиональной деятельности.
Ключевые слова: мотивация к учебной деятельности, интеграционные связи, тригонометрия.
Согласно утвержденной Концепции развития математического образования в Российской Федерации одной из проблем развития математического образования является проблема мотивационного характера, которая заключается в наличии низкой учебной мотивации школьников [1]. В свою очередь, сформированность мотивации к обучению является одним из основных требований к результатам освоения основной образовательной программы основного общего образования. Личностные же результаты должны отражать формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению [2].
Федеральный государственный образовательный стандарт общего образования для достижения целей образования предусматривает установление интеграционных связей между различными учебными дисциплинами в школе, а также подчеркивает многосторонность результатов освоения обучающимися основной образовательной программы, отмечая наряду с предметными и личностными, важность и метапредметных результатов [3].
Перспективным решением проблемы мотивационного характера служит реализация интеграционных связей математических дисциплин как с другими учебными дисциплинами, так и с различными сферами человеческой деятельности. На необходимость построения педагогического процесса на основе идей интеграции ориентируют работы Ю. К. Бабанского, В. С. Безруковой, В. В. Гузеева, А. Я. Данилюка, И. Я. Лернера, В. Т. Фоменко и многие другие [4, c. 5].
Под интеграционными связями математики будем понимать различные её взаимодействия как с другими учебными дисциплинами, так и со сферами человеческой деятельности.
В данной статье рассмотрим некоторые возможности построения процесса изучения тригонометрии как раздела школьного курса математики на основе реализации идей интеграции.
Пример 1. Тригонометрия и астрономия.
Тригонометрические величины широко применимы в астрономии. Так, например, способ вычисления расстояний между Землей и Луной был реализован при помощи определенных знаний тригонометрии (рис. 1):
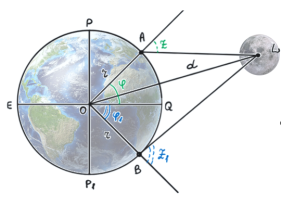
Рис. 1. Иллюстрация к выводу формулы расстояния между Землей и Луной
Пусть
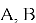
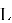
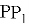
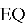
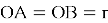
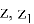
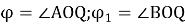
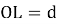
Из треугольников ALO и BLO имеем:
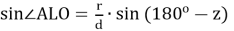
и
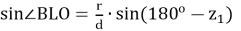
Но так как
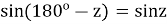
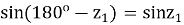
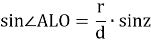
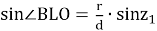
Для Луны углы ALO и BLO каждый меньше одного градуса, поэтому без особой погрешности синусы этих углов можно заменить дугами им соответствующими:
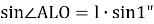
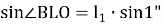
где
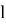
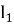
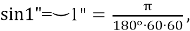
Тогда:
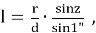
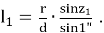
Для четырехугольника AOBL, сумма внутренних углов которого равна четырем прямым, можем написать:
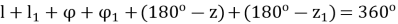
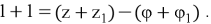
Сложив почленно равенства (3) и (4), находим:
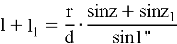
Следовательно:
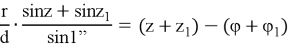
Откуда окончательно получаем:
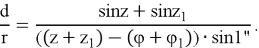
То есть искомое расстояние выразится в частях земного радиуса.
Кроме этого, пользуясь данными тригонометрии, астрономы научились решать и более сложные задачи — рассчитывать радиусы небесных светил и многие другие.
Пример 2. Тригонометрия и измерения на поверхности Земли.
Тригонометрия применяется при измерениях на поверхности Земли. Так, например, без тригонометрии было бы невозможно определение высоты фабричной трубы, определение расстояния между двумя недоступными точками, решение задач навигации, а также триангуляция.
Например, неровности земной поверхности и препятствия в виде гор, болот, лесов и рек раньше заставляли ограничиваться измерением незначительных расстояний, и, следовательно, при таких условиях вопрос об истинных размерах земного шара не мог быть разрешен сколько-нибудь удовлетворительно. В XVII веке голландский ученый Снеллиус (1580–1626) предложил для этой цели прием, называемый «триангуляцией», имеющий огромную практическую ценность, так как он освобождает от необходимости непосредственного измерения линий значительного протяжения на земной поверхности. В свою очередь, данный прием был применим только со знаниями тригонометрии, так как его применение включало в себя решение целой сети треугольников.
Пример 3. Тригонометрия и физика.
Тригонометрия получила широкое применение в физике, в первую очередь, для описания периодических процессов, в частности, гармонических колебаний. Например, координата тела
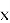
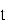
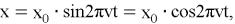
где
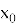
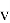
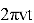
Также тригонометрия используется при разложении и сложении физических сил, определении коэффициента преломления, а также помогает в решении многих физических задач и используется в исследованиях баллистического движения [5].
Пример 4. Тригонометрия и биология.
Тригонометрия также используется в биологии для описания периодических процессов. Например, для описания биоритмов. Биологические ритмы — периодические повторяющиеся изменения характера и интенсивности биологических процессов и явлений. Биоритм представляет собой последовательность повторяющихся циклов, а цикл, в свою очередь, это завершенное колебание, отклонение определенного показателя от исходной величины с возвратом к ней через некоторое время.
Пример 5. Тригонометрия и медицина.
Тригонометрия играет важную роль в таком разделе медицины как кардиология. Например, иранские ученые нашли способ систематизировать информацию, связанную с электрической активностью сердца. Сделать это им удалось в результате вывода комплексного алгебраически-тригонометрического равенства, которое состоит из 8 выражений, 32 коэффициентов и 33 параметров, включающих в себя и дополнительные, необходимые для расчета в случаях аритмии. В средствах массовой информации и в среде ученых это равенство получило красноречивое название «формула сердца» [5].
Кроме того, тригонометрия имеет различные связи с различными областями человеческой деятельности: архитектура, техника и артиллерия.
В нашем исследовании планируется запись серии видео-уроков, демонстрирующих интердисциплинарные и интродисциплинарные связи тригонометрии. Запись будет осуществляться на базе современной студии самозаписи Института математики, механики и компьютерных наук им. И. И. Воровича Южного федерального университета. Таким образом, при просмотре созданных видеороликов, увидев практическое применение тригонометрии при изучении её интеграционных связей, учащиеся смогут не только повысить уровень мотивации к учебной деятельности, но и сделать более обдуманный шаг в сторону выбора своей будущей профессиональной деятельности.
Литература:
- Концепция развития математического образования в Российской Федерации. URL: 41d4b63b1dd474c16d7a.pdf (government.ru) (дата обращения: 22.01.2025).
- Федеральный Государственный Образовательный Стандарт. URL: ФГОС Основное общее образование — ФГОС (fgos.ru) (дата обращения: 29.01.2025).
- Дзреян, Т. Х. Научно-исследовательская работа «Реализация интеграционных связей математики с предметами естественнонаучного цикла». URL: Научно-Исследовательская работа «Реализация интеграционных связей математики с предметами естественнонаучного цикла». | Образовательная социальная сеть (nsportal.ru) (дата обращения: 12.02.2025).
- Жмурова, И. Ю. Интеграционные связи дискретной математики как средство повышения эффективности профессиональной подготовки бакалавров физики-математического образования: автореф. дис. кан. наук. — Ростов-на-Дону.:2005.-24 с.
- Валько, С. Ю. Тригонометрия вокруг нас / С. Ю. Валько, М. Н. Симакова. — Текст: непосредственный // Юный ученый. — 2023. — № 6 (69). — С. 77–82. — URL: Тригонометрия вокруг нас | Статья в журнале «Юный ученый» (moluch.ru) (дата обращения: 18.02.2025).







