Геостационарная орбита (ГСО) — это круговая орбита, находящаяся на высоте 35 786 км над уровнем моря, в экваториальной плоскости. Спутники, находящиеся на этой орбите, движутся с угловой скоростью, совпадающей с угловой скоростью вращения Земли, и поэтому остаются практически неподвижными относительно наземных наблюдателей. Поэтому эта орбита является в первую очередь критической орбитой для спутников связи. В настоящее время на этой орбите находится более 580 искусственных спутников. Расстояние между некоторыми из них составляет всего 0,1 0 , то есть они находятся на расстоянии 73 км друг от друга. Это подчеркивает необходимость точного определения параметров их орбиты для надлежащего управления ими и, как следствие, направления маневров в нужное время и в нужном направлении.
ГСО активно используется для спутниковой связи , метеорологии , наблюдения за Землёй и других задач. Однако движение спутников на этой орбите подвержено возмущениям, которые вызывают отклонения от номинального положения, требующие регулярных коррекций.
Цель данной работы — рассмотреть параметры геостационарной орбиты, основные виды возмущений, методы их компенсации и провести сравнение теоретических орбитальных параметров с измеренными параметрами.
Координаты, используемые для расчета параметров орбиты геостационарного спутника.
Планеты, включая Землю, движутся вокруг Солнца по эллипсам, совершая полный оборот за 365,25 суток. Искусственные спутники на геостационарной орбите движутся по квазикруговой траектории, совершая один оборот каждые 86 164 секунды. Для определения параметров орбиты спутников, работающих на этой орбите, используются различные системы координат. Для определения параметров орбит современных искусственных спутников Земли, особенно находящихся на геостационарной орбите, используется GTOD (Gamma True of Date) координат, центр которой совпадает с центром масс Земли.
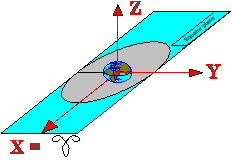
Рис. 1
GTOD:
Z = мгновенная ось вращения Земли (близкая к оси полюса Юг-Север);
X = в плоскости, перпендикулярной Z (экваториальной плоскости), в направлении γ;
γ = весенняя точка
= направление на Солнце в день весеннего равноденствия;
Y = перпендикулярно X в экваториальной плоскости.
GTOD не является полностью инерциальной системой отсчета, то есть она не фиксирована относительно звезд. Поэтому для упрощения расчетов при расчете орбиты спутника используется средняя система координат 2000 года — J2000.
Основные параметры геостационарной орбиты
Геостационарная орбита — это частный случай геосинхронной орбиты, и её параметры строго определены:
– Радиус орбиты:
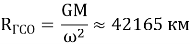
где G– гравитационная постоянная, M — масса Земли, ω — угловая скорость вращения Земли.
– Высота над поверхностью Земли:

– Орбитальная скорость:
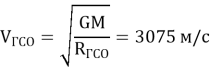
– Период обращения:
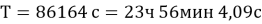
– Наклонение орбиты:
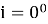
– Эксцентриситет:
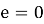
Описанные выше параметры геостационарной орбиты являются теоретическими значениями, поэтому спутник на ГСО движется по почти круговой орбите, оставаясь над одной и той же точкой на экваторе. Однако в действительности искусственные спутники, движущиеся по геостационарной орбите, не являются абсолютно устойчивыми относительно Земли, поскольку они смещаются от точки своей орбиты из-за различных гравитационных и других воздействий.
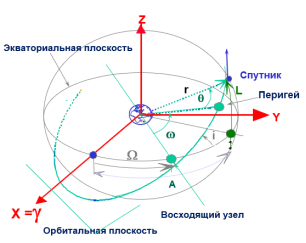
Рис. 2
Определение орбиты в космосе:
S = спутник; r = радиус орбиты; A = восходящий узел; i = наклонение;
= прямое восхождение восходящего узла (RAAN); = аргумент
перигея; = истинная аномалия; L = широта.
Для определения одной точки и ее скорости в космической пространстве необходимы 6 параметров.
В механике Кеплера используются следующие параметры:
a, e: размер и форма орбиты; i, : плоскость орбиты; : ориентация орбиты в ее плоскости; M (or ): положение спутника.
Теоретически возможные значения параметров Кеплера следующие:
a = 42165.765 km; e = 0; i = 0; = от 0° до 360°; = от 0° до 360°; M = от 0° до 360°.
Однако в реальных расчетах описанные выше 6 параметров для геостационарной орбиты напрямую не применимы, поскольку:
если i = 0, не может быть определено;
если e = 0, невозможно определить.
Таким образом, наиболее основными адаптированными параметрами, используемыми при определении параметров орбит геостационарных спутников, являются следующие.
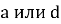
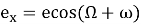
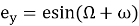
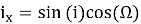
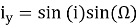
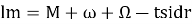
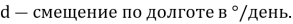
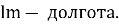
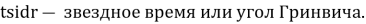
Ось X = ось весеннего равноденствия γ (Рис. 3., A);
Полярные координаты:
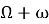
Декартовы координаты: e x , e y ;
Вектор эксцентриситета направлен перигей.
Ось X = ось весеннего равноденствия γ (Рис. 3., B);
Полярные координаты
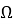
Декартовы координаты: i x , i y ;
Вектор наклона направлен на восходящий узел.
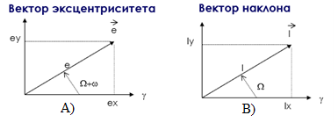
Рис. 3
Основные виды возмущений орбиты
Геостационарная орбита не является абсолютно стабильной. На движение спутника влияют гравитационные и негравитационные факторы, вызывающие отклонения от номинального положения.
Закон Ньютона верен только в случае чистого притяжения «одного центрального тела». Но эта гипотеза не полностью проверена для геостационарного спутника:
Масса Земли не сосредоточена в одной точке;
Существует также притяжение Луны и Солнца;
Спутник подвергается потоку частиц, исходящих от Солнца: солнечному ветру и солнечное давление.
Это создает «орбитальные возмущения», так что орбита не совсем кеплеровская. Из-за этих возмущений геостационарный спутник, который не контролируется, будет дрейфовать от своего номинального положения. Эти орбитальные возмущения являются причиной маневры удержания станции.
Гравитационные возмущения Земли
Земля имеет несферическую форму, что приводит к изменению её гравитационного потенциала.
Эти факторы вызывают дрейф долгот спутников, что приводит к образованию:
–
Стабильных долгот
:
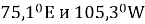
–
Нестабильных долгот
:
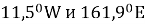
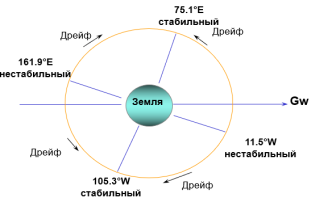
Рис. 4
Влияние гравитационного потенциала Земли на большую полуось и долготу :
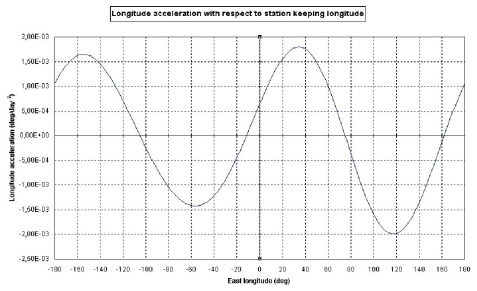
Рис. 5
Влияние Луны и Солнца
Притяжение Луны и Солнца влияет на наклонение орбиты. В среднем наклонение увеличивается со скоростью:
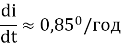
Этот эффект циклический, с периодом 18.6 лет . Для контроля этого возмущения необходимы маневры север/юг, и эта дельта-v меняется ежегодно, как показано на графике ниже.
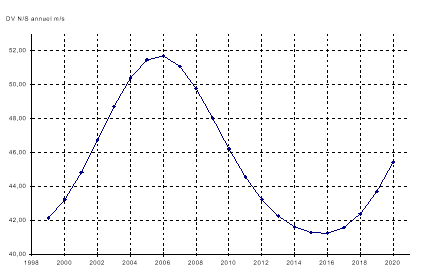
Рис. 6
Давление солнечного излучения
Солнечное давление зависит от нескольких факторов, таких как положение Солнца относительно спутника, масса спутника, площадь поверхности спутника, а также отражающие и рассеяющие свойства материалов, из которых изготовлена поверхность спутника. Основной проблемой при расчёте солнечного давления является точное определение расстояния между спутником и Солнцем в каждый момент времени, а также учёт угла падения солнечных лучей. Солнечное излучение оказывает слабое, но кумулятивное влияние на орбиту спутника. Основной эффект — изменение эксцентриситета орбиты:
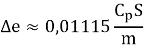
где C p — коэффициент давления, S– площадь спутника, m — его масса.
Этот эффект также приводит к колебаниям широты спутника.
Коррекция орбиты и поддержание положения
Возмущения требуют регулярной коррекции орбиты, которая выполняется с помощью реактивных двигателей спутника. Удержание геостационарной станции заключается в контроле долготы и широты спутника в заданных пределах, что определяет «орбитальное окно удержания станции».
Операции могут быть организованы на постоянной временной основе, цикл содержания станции. Пример типичного 14-дневного цикла:
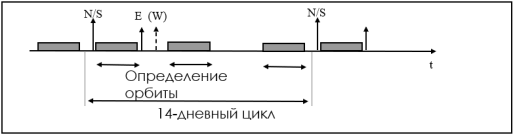
Рис. 7
День 0: маневр на север или юг; Дни 0–3: после маневра севера/юг, кампания по измерению локализации (48 ч); День 3: маневр на восток или запад (+ при необходимости, запад или восток примерно через 12 ч); Дни 3–5: после маневра(ов) восток/запад, кампания по измерению локализации (48 ч); Дни 10–12: кампания по измерению локализации (48 ч) перед маневром севера/юг следующего цикла.
Коррекция наклонения (N/S манёвры)
Используется для компенсации наклонения i, вызванного воздействием Луны и Солнца. Манёвры выполняются каждые 14 дней, с ежегодным расходом топлива около 45 кг. Для коррекции наклона примерно 1 м/с дельта-v потребуется 1 кг топлива.
Коррекция долготного дрейфа (E/W манёвры)
Используется для управления долготой спутника.
Если спутник дрейфует со скоростью d градусов в день, необходимо выполнить манёвр. Коррекция выполняется раз в 7–14 дней.
Коррекция эксцентриситета
Выполняется при возмущениях солнечного давления. Используется метод двойного манёвра, когда выполняются два коррекционных импульса с разницей во времени 12 часов.
Заключение
Геостационарные спутники подвергаются различным возмущениям, включая гравитационные эффекты Земли, воздействие Луны и Солнца, а также давление солнечного излучения. Эти факторы приводят к изменению параметров орбиты и требуют регулярных корректировок.
Правильное планирование орбитального обслуживания позволяет минимизировать расход топлива и продлить срок службы спутников, обеспечивая их стабильное функционирование на ГСО.
Литература:
- Документы по орбитальной динамике компании «Thales Alenia Space» для геостационарного спутника.— 2014.
- Oliver Montenbruck and Eberhard Gill “Satellite Orbits” 1st Edition 2000y.
- Gerard Maral “Satellite communications systems” — 2009.
- Howard D. Curtis “Orbital Mechanics for Engineering Students” First published 2005y.







