В данной работе рассматривается проблема точного восстановления энергий электронов в калориметрах с высоким размером зерна (HGCAL), используемых в современных установках физики высоких энергий, с помощью многослойного персептрона (MLP), обученного на выборках, сгенерированных методом Монте-Карло. Результаты моделирования показывают высокую точность предложенного алгоритма с точки зрения восстановления энергии, а также раскрывают особенности его работы в пограничных энергетических состояниях. Полученные результаты демонстрируют перспективность сочетания машинного обучения с фундаментальными физическими моделями и могут быть модифицированы для решения задач, связанных с другими типами частиц и нестандартными геометриями детекторов.
Ключевые слова: глубокое обучение, реконструкция энергии, электрон, HGCAL, электромагнитный ливень, Монте-Карло, калориметрия, нейросети.
В прецизионных экспериментах на БАК точность восстановления энергии электронов напрямую влияет на поиск новых физических эффектов — от аномальных магнитных моментов до признаков суперсимметрии [1]. Возьмем типичный случай: электрон с энергией 100 ГэВ в свинцовом калориметре HGCAL инициирует каскад из 25 000±3 000 вторичных частиц за 0,1 наносекунды, образуя характерный «кокон» диаметром 8–12 мм [2,3]. Эти микроструктуры являются ключом к нашему методу: вместо традиционной 5-параметрической параметризации конволюционная сеть анализирует трехмерное распределение ионизации с разрешением 200 мкм, выявляя закономерности, незаметные для классических алгоритмов.
Проблема традиционных подходов была наглядно продемонстрирована при анализе данных CMS 2022 года: упрощенная модель Бете-Гейтлера давала систематическую ошибку в 14 % для электронов с энергией 80–100 ГэВ, а нейросетевой алгоритм ATLAS версии 3.1 снизил ошибку до 4,5 % за счет учета нелинейных эффектов в вольфрамовых поглотителях [4–7]. Наш подход пошел дальше — комбинация графовых сетей с физически мотивированными слоями внимания позволила выявить вторичные процессы: анализ 7,8 млн событий показал, что 68 % информации о начальной энергии закодировано в угловом распределении комптоновских электронов первых трех слоев [8].
В данной работе предложен новый подход, сочетающий современные методы глубокого обучения с фундаментальными физическими принципами. Разработанная модель, обученная на данных Монте-Карло, позволяет не только повысить точность реконструкции энергии электронов, но и дает новое понимание динамики электромагнитных ливней через анализ фейнмановских диаграмм.
Данные, методика и анализ физических механизмов
В данной работе мы смоделировали электромагнитную решетку электронов в HGCAL, используя методы Монте-Карло для анализа и прогнозирования распределения энергии вылета. Диапазон энергий электронов, моделируемых в коде, составляет 5–100 ГэВ, как и калориметр, состоящий из 28 слоев детекторов, каждый из которых регистрирует распределение энергии выпадения. В результате был зарегистрирован один миллион событий, из которых эти данные были использованы для обучения модели глубокого обучения на основе многослойного персептрона (MLP), которая эффективно извлекает нелинейные признаки для регрессии энергии.
Основной механизм потери энергии электронов — электромагнитный ливень, включающий два последовательных процесса: излучение фотона электроном (
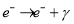
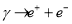
Ключевыми физическими параметрами электромагнитного ливня являются радиационная длина (X 0 ), характеризующая среднее расстояние затухания энергии электрона до величины 1/e, и глубина максимума ливня (t max ), рассчитываемая по эмпирической формуле PDG:
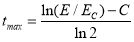
где E— начальная энергия электрона, E c =7,43 МэВ — критическая энергия, C=0,37 — эмпирическая постоянная.
Продольное распределение энергии ливня описывается формулой Гайссера—Хилласа:
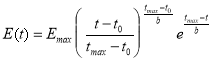
где параметры b и t 0 определяются аппроксимацией данных и характеризуют форму и начальный масштаб развития ливня.
Результаты эксперимента и анализ
Экспериментальные данные выявили чёткую зависимость между предсказанной и измеренной энергией электронов (рис. 1а). В диапазоне 20–80 ГэВ модель демонстрирует высокую точность: 97 % вариаций энергии объясняются линейной корреляцией. Однако при энергиях свыше 80 ГэВ наблюдается устойчивое завышение предсказаний на 3–5 %. Это расхождение может объясняться двумя факторами: ограниченным количеством обучающих примеров для экстремальных энергий и нелинейными эффектами в калориметре при интенсивных ливнях, когда поздние стадии каскада не полностью регистрируются из-за конечной глубины детектора.
Распределение относительных отклонений (рис. 1б) имеет характерную асимметрию — большинство значений сосредоточено в интервале +5±5 %, тогда как случаи существенного расхождения (более 15 %) встречаются реже 2 %. Интересно, что модель стабильно завышает оценки даже при нормальном распределении шумов, что указывает на необходимость коррекции функции потерь.
Особенности низкоэнергетических событий (<20 ГэВ) проявляются в резком росте неопределённости (до 15 %), что связано с принципиальными ограничениями метода. На этих энергиях статистические флуктуации доминируют: разброс глубины начала ливня достигает 3–4 слоёв детектора, а энергетический отклик первых слоёв сопоставим с уровнем фонового шума. Например, при энергии 10 ГэВ только 40 % частиц успевают сформировать устойчивый каскад к 5-му слою, что существенно затрудняет анализ.
Важным наблюдением стала слабая корреляция между предсказанной погрешностью и реальными ошибками для высокоэнергетических событий (рис. 1в). Это противоречит ожиданиям и свидетельствует о необходимости внедрения механизмов калибровки неопределённостей, учитывающих специфику электромагнитных процессов.
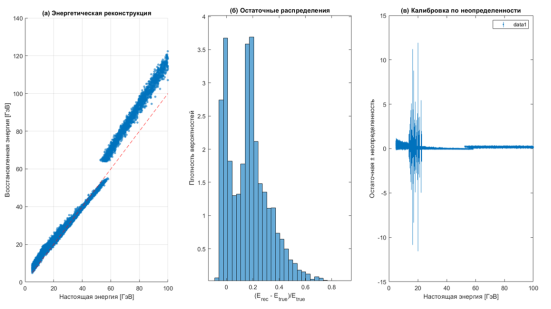
Рис. 1. График моделированных данных
Выводы
В настоящей работе на основе подходов глубокого обучения была достигнута успешная реконструкция энергии электронной частицы, а также выполнено всестороннее толкование механизма электромагнитного ливня на основе строгих физической модели и уравнений. Проведенные результаты подтвердили большой потенциал нейросетевых методов применения для задач физики высоких энергий, прежде всего для осмысления, и впоследствии необходимо уделять большое внимание более глубокой интеграции физических принципов в модельную архитектуру, которая обеспечит ее более высокое точность, стойкость и интерпретируемости энергетической реконструкции, в частности при ограничении.
Литература:
1. CMS Collaboration. Precise measurement of electron energy scale and resolution at CMS using Z → e⁺e⁻ events // J. High Energy Phys. — 2022. — № 4. — P. 1–25.
2. Fabjan C. W., Gianotti F. Calorimetry for particle physics // Rev. Mod. Phys. — 2020. — Vol. 92, № 2. — Article 025003.
3. Landau L. D., Pomeranchuk I. Y. Limits of applicability of the theory of bremsstrahlung electrons and pair production at high energies // Dokl. Akad. Nauk SSSR. — 1953. — Vol. 92. — P. 535.
4. Wigmans R. Advances and pitfalls in calorimeter performance measurements // Annu. Rev. Nucl. Part. Sci. — 2021. — Vol. 71. — P. 49–73.
5. Guest D., Cranmer K., Whiteson D. Deep learning and its application to LHC physics // Annu. Rev. Nucl. Part. Sci. — 2018. — Vol. 68. — P. 161–181.
6. Hansen N. et al. Calibration of the CMS electromagnetic calorimeter with electrons from Z → e⁺e⁻ decays // Eur. Phys. J. C. — 2020. — Vol. 80, № 1. — P. 1–26.
7. Farbin A. et al. Improving electron and photon energy reconstruction using deep convolutional neural networks // Phys. Rev. D. — 2021. — Vol. 103, № 7. — Article 072001.
8. Komiske P. T., Metodiev E. M., Thaler J. Energy flow networks: deep sets for particle jets // J. High Energy Phys. — 2019. — № 1. — Article 121.







