Об одной задаче идентификации функции источника двумерного псевдопараболического уравнения третьего порядка



В данной статье изучается задача идентификации источника специального вида в двумерном псевдопараболическом уравнении в случае задачи Коши. В классе достаточно гладких ограниченных функций доказывается теоремы существование и единственности решения.

Для построения решение обратной задачи используется преобразование Фурье, метод операторных уравнений Вольтерра. В работе исследуется вопрос об однозначной разрешимости рассматриваемой обратной задачи для псевдопараболического уравнения.

Ключевые слова: задача идентификации источника, обратные задачи, псевдопараболическое уравнение, преобразование Фурье, метод операторных уравнений Вольтерра, однозначная разрешимость.

This article studies the problem of identifying a source of a special type in a two-dimensional pseudoparabolic equation in the case of the Cauchy problem. In the class of sufficiently smooth bounded functions, the existence and uniqueness theorems of the solution are proved. The Fourier transform and the Volterra operator equation method are used to construct the solution to the inverse problem. The paper studies the question of the unique solvability of the inverse problem under consideration for the pseudoparabolic equation.

Keywords: source identification problem, inverse problems, pseudoparabolic equation, Fourier transform, Volterra operator equation method, unique solvability.

Введение

В этой работе исследована задача идентификации функции источника специального вида в двумерном псевдопараболическом уравнении в случае данных Коши. Существование и единственность решения обратной задачи доказывается в классах гладких ограниченных функций. Для исследования задачи применяется метод, позволяющий, свести исходную обратную задачу к прямой задаче для нагруженного псевдопараболического уравнения [1, 2]. Существование решения прямой задачи доказано с помощью фундаментального решения двумерного псевдопараболического уравнения

[2–4]. Задача идентификации функции источника, зависящей от ( t,x ), рассмотрена в работе [5]. В [2] изучен случай, когда условия переопределения задаются на гладкой кривой, а неизвестная функция источника зависит лишь от временной переменной. Краевые задачи идентификации функции источника исследованы в работах [6, 7].

Примем следующие обозначения; и

точки в , , .

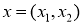
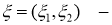
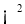
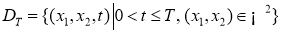
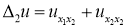
Постановка задачи и формулировка основного результата.

Рассмотрим в области задачу Коши

(1)

(2)

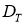
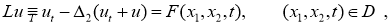
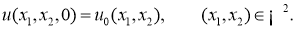
Здесь — действительные заданные функции.

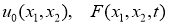
Задача определения функцию из условий (1)-(2) что при заданных достаточно гладких функциях , называется прямой задачей.

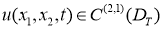
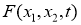
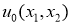
Определение 1. Функцию будем называть классическим решением задачи (1) — (2), если она удовлетворяет уравнению (1), начальному условию (2) в классическом смысле.

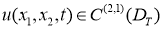
Пусть

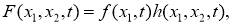
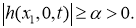
Обратная задача. Требуется найти пару функций

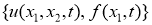
из соотношений (1) -(2), если она удовлетворяют следующему условию переопределения

(3)

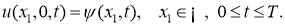
где — заданная функция.

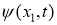
Для прямой задачи (1) -(2) справедлива (см. [2,4])

ТЕОРЕМА 1 . Если и финитна по в

, то классическое решение задачи Коши (1), (2) существует единственно и дается формулой

(4)

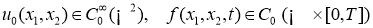
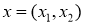
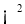
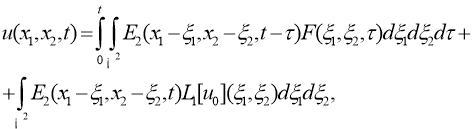
где

фундаментальное решение оператора , функция - функция Макдональда.

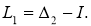
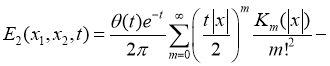
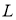
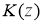
Приведем задачу (1) -(3) к некоторой вспомогательной прямой задаче. Для этого положим в уравнении (1). Учитывая условие (3), получим соотношение

. (5)

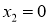
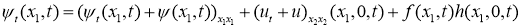
Из (5) находим

(6)

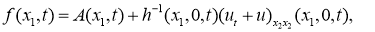
Здесь

- известная функция.

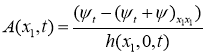
Подставляя функцию в уравнение (1), приходим к задаче Коши для линейного нагруженного уравнения

(7)

(8)

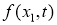
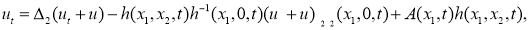
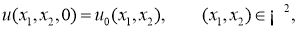
Вводя обозначение , из задачи (7)-(8), получим

(9)

(10)

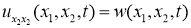
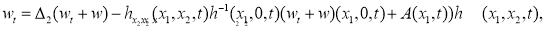
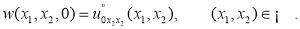
Докажем разрешимость задачи (9),(10).

Используя фундаментальное решение оператора

,

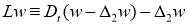
решение задачи (9), (10) в виде

(11)

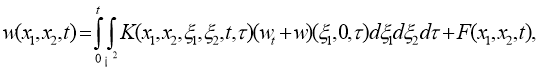
где

,

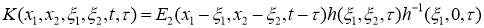
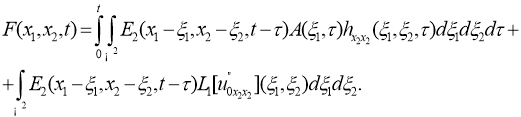
Введем новую неизвестную функцию . Тогда

будет удовлетворять условиям

(12)

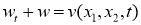
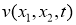
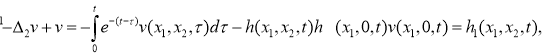
где

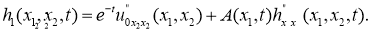
Приведем некоторые вспомогательные материалы.

Рассмотрим уравнение

(13)

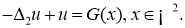
Определение 1. Обобщенная функция

, удовлетворяющая уравнению называется фундаментальным решением оператора .

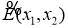
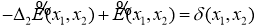
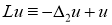
Лемма 1. Функция

(14)

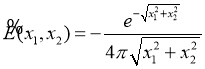
является фундаментальным решением оператора .

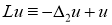
Доказательство. Справедливы следующие равенства.

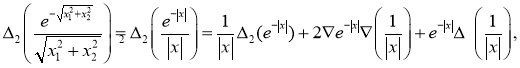
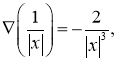
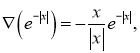
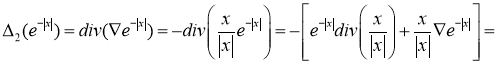
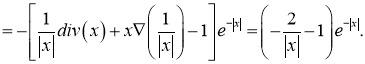
Из этих равенств следует соотношение

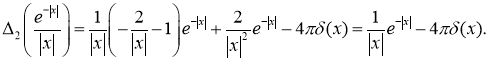
Поэтому имеет место равенство

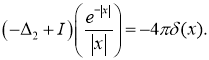
Следовательно, функция удовлетворяет равенству

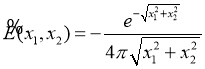
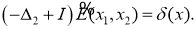
и поэтому является фундаментальным решением оператора .

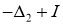
Справедлива

Лемма 2. Если и финитна, то

(15)

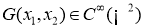
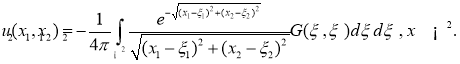
является решением уравнения (13).

Доказательство. Если - фундаментальное решение оператора , то

(16)

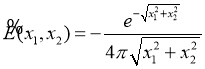
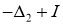
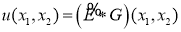
решение уравнения (13). В самом деле,

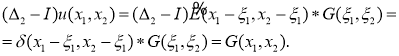
свертки в данном случае существуют благодаря финитности функции . Формула (16) с учетом (14), эквивалентна равенствам (13), (14).

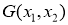
Продолжим доказательство теоремы 1.Обращая в уравнении (12) оператор , получим

(17)

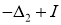
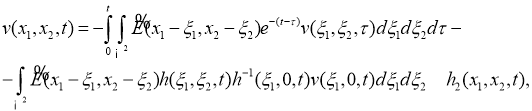
где

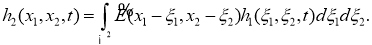
Положив в (16) получим

(18)

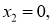
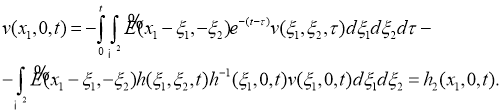
Система (17), (18) представляет собой линейную систему интегральных уравнений Вольтерра-Фредгольма второго рода относительно функций и , которое имеет единственное решение в классе гладких и ограниченных функций.

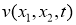
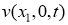
Таким образом, справедлива

Теорема 1. Пусть функции , , , кроме того,

. Тогда существует единственное решение обратной задачи (1) -(3).

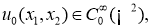
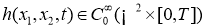
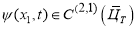
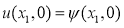
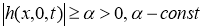
Литература:

1. Аблабеков, Б. С. Обратные задачи для дифференциальных уравнений третьего порядка. — LAP.LAMBERT Academic Publishing 2011. –291 с.
2. Аблабеков Б. С. Фундаментальное решение задачи Коши для двумерного уравнения фильтрации жидкости в трещиновато-пористой среде//Известия КГТУ им.И.Раззакова, № 9, Бишкек 2009. — С.8–101.
3. Аблабеков, Б. С. Метод полуобращения и существование решений начальной, начально-краевой задачи // Наука и новые технологии. –1999.- № 4. — С. 12– 19.
4. Аблабеков, Б. С. Явное решение задачи Коши для двумерного псевдопараболического уравнения [Текст] / Б. С. Аблабеков, А. Б. Байсеркеева //Известия ВУЗов Кыргызстана. 2015. № 10. С. 3–7.
5. Белов, Ю. Я. Некоторые задачи идентификации коэффициентов полу линейных параболических уравнений [Текст] / Ю. Я. Белов, И. В. Фроленков //Докл. РАН, 404(2005), № 5, 583–585