1. Introduction
The mathematical framework of fractional-order integro-differentiation provides a powerful tool for modeling systems in which nonlocal properties in both time and space are significant. Fractional derivatives allow for the inclusion of memory effects (temporal nonlocality) and spatial correlations (spatial nonlocality), leading to their widespread application in the natural sciences.
Equations with fractional derivatives describe the evolution of physical systems with inherent losses. The order of the derivative reflects the degree to which the system's states are retained over time. Such «residual memory» systems occupy an intermediate position between systems with complete memory and memoryless Markov systems.
The classical treatment of compressible fluid flow and conservation laws in multiple spatial variables is comprehensively presented in [5], which serves as a foundational reference for this area of mathematical physics.
Fractional calculus is a branch of mathematical analysis concerned with derivatives and integrals of arbitrary (including real) order. One of its key applications is the study and solution of differential equations involving fractional derivatives.
In modeling continuous media with memory, equations emerge that describe a new class of wave phenomena that lie between classical diffusion and conventional wave propagation [1], [2].
Fractional differentiation is understood as a combination of differentiation and integration. In this paper, we address a boundary value problem for the wave equation involving the Riemann–Liouville fractional derivative in the upper half-plane. The initial conditions are also expressed in terms of fractional derivatives. The solution involves applying the Fourier transform with respect to the spatial variable, followed by the Laplace transform in time, and then performing the respective inverse transforms. Finally, two limiting cases of the fractional order are analyzed and discussed.
2. Preliminaries
This section will present the definition of fractional derivative in the Riemann-Liouville sense, the Mittag-Leffler function, the Laplace and Fourier transforms for fractional derivative, which will be used in solving the problem.
2.1. Riemann-Liouville Fractional Derivatives
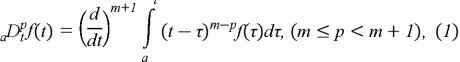
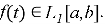
This expression is the best known definition of the fractional derivative, usually called the fractional derivative in the Riemann-Liouville sense [3].
2.2. Mittag-Leffler type functions
A two-parameter function of Mittag-Leffler type is defined by the expansion of the series [3]
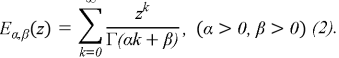
2.3. Boundary value problem for the wave equation. Green's function
In [6], the author investigated a fractional wave equation involving fractional derivatives of the same order
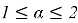
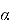
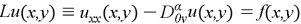
When the boundary conditions are satisfied and
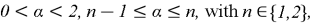
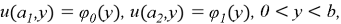
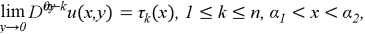
Where
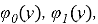
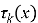
The function
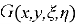
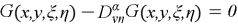
and satisfy
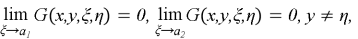
Let us call the Green's function of the first boundary value problem for the wave equation. These properties are also satisfied by the function
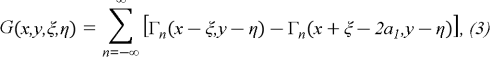
where
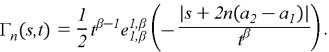
3. Problem Formulation and Formal Solution
In the domain
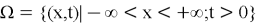
find the solution of equation:
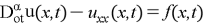
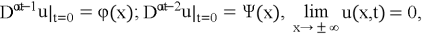
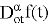
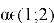
Theorem. Function
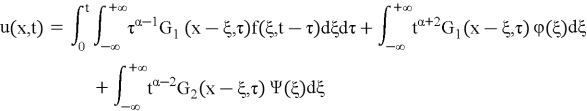
where
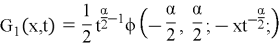
and
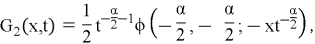
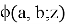
Proof :
We apply the Fourier transform to the equation (4)-(5) with respect to the variable
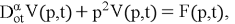
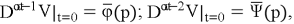
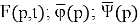
We apply the Laplace transform to equation (6) with respect to the variable t, taking into account conditions (7). We obtain:
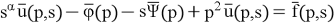
where
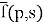
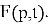
We apply the inverse Laplace transform with respect to the variable
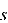
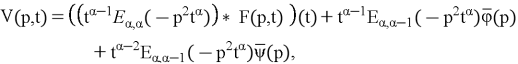
where
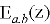
Now, we apply the inverse Fourier transform with respect to the variable
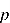
Applying the inverse Laplace transform with respect to
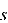
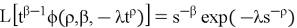
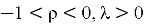
with
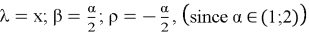
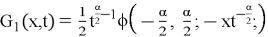
Applying the inverse Laplace transform again, using the formula (14) with
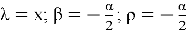
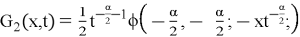
Substituting equations (15) and (16) into the equation (10), we obtain the solution of the original problem (4)–(5).
Limiting cases of the fractional derivative order
Let us now consider the limiting cases of the fractional derivative order for
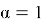
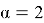
Case
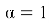
The problem (4)-(5) takes the form:
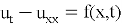
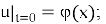
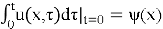
The solution to the problem (17)–(18) in domain
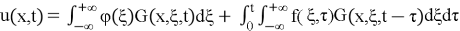
where the Green's function (3),
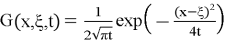
It is shown that for
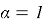
Case
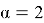
Then the problem (4)–(5) becomes:
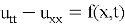
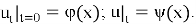
The solution is given by [5]:
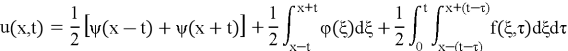
(22)
Thus, the final expression becomes:
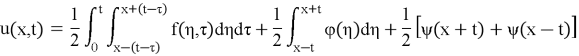
It is shown that for
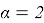
References:
- [1] Nakhushev, A. M. Fractional Calculus and Its Applications / Nakhushev, A. M. — 1st ed. — Moscow: Fizmatlit, 2003. — 320 c.
- Olemskoy, A. I., Flat, A. Ya. Application of the Fractal Concept in Condensed Matter Physics / Olemskoy, A. I., Flat, A. Ya. — 1st ed. — Moscow: Uspekhi Fizicheskikh Nauk, 1993. — Vol. 163, No. 12. — 50 c.
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications / Podlubny, I. — 1st ed. — San Diego: Academic Press, 1999. — 340 c. — (Mathematics in Science and Engineering; Vol. 198).
- Gradshteyn, I. S., Ryzhik, I. M. Table of Integrals, Series, and Products / Gradshteyn, I. S., Ryzhik, I. M. — 4th ed. — Moscow: Fizmatgiz, 1963. — 1100 c.
- Majda, A. J. Compressible Fluid Flow and Systems of Conservation Laws in Several Variables / Majda, A. J. — 1st ed. — New York: Springer-Verlag, 1984. — 551 c.
- Luchko, Yu. Fractional Wave Equation and Damped Waves / Luchko, Yu. — 1st ed. — New York: Journal of Mathematical Physics, 2013. — Vol. 54, 031505.
- Pskhu, A. V. Boundary Value Problems for Partial Differential Equations of Fractional and Continuous Order / Pskhu, A. V. — Doctoral dissertation. — Moscow: Moscow State University, 2009. — 320 p.







