Рассматривается задача исследования колебаний прямоугольной мембраны. Показана неэффективность использования аналитических подходов. Для решения этой задачи были разработаны и использованы специальные алгоритмы численных методов.
Ключевые слова: мембрана, колебания системы, разностная схема, эффективность.
Введение. В современном мире ежедневно появляются сотни новых технологий, о которых мы либо ничего не знаем, либо просто-напросто игнорируем в силу того, что слабо понимаем, как это может помочь нам в осуществлении ежедневных задач, будь то бытовых или научных.
Казалось бы, что может быть ещё интересного в исследовании уравнений математической физики, ведь тема исчерпала себя. Большинство открытий в этой области были сделаны десятилетия назад. Но оказывается, мы можем улучшить эффективность старой теории новыми подходами, использование которых для практики имеет неоспоримое преимущество.
Исследование колебаний и незамедлительная реакция на разрушительные воздействия от них имеет важную не только научную, но практическую значимость для общества. Сколько можно было бы предотвратить несчастных случаев, если бы удалось предотвратить разрушение механических конструкций в связи с внешним воздействием. Необходимо создавать инструменты, которые позволяли бы будучи встроены в технику предотвращать подобные явления или предупреждать о них заранее. Но для этого необходимо научиться быстро анализировать колеблющиеся процессы и оценивать дальнейшее развитие ситуации, что требует модификации в существующих подходах.
В этой работе будет показан новый подход к решению этой задачи на основе численных методов на примере колебаний прямоугольной мембраны, которые позволят не только выйти за рамки классических решений, но и увеличат скорость реагирования в десятки раз.
Постановка задачи. Колебания прямоугольной мембраны описываются гиперболическим уравнением [1]
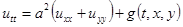 ,
, 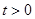 ,
,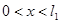 ,
,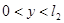 ,
,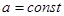 (1)
(1)
Начальные отклонения и скорость распространения колебания мембраны
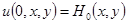 , (2)
, (2)
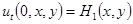 (3)
(3)
будем рассматривать как начальные условия. На границе прямоугольной мембраны наложим условие закрепления согласно
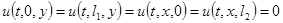 (4)
(4)
В данной работе мы будем исследовать колебательные процессы и возможность построения более удобного алгоритма получения решения уравнения колебаний прямоугольной мембраны, что позволит встроить этот алгоритм в специально сконструированный прибор, использующийся для гашения.
Аналитический метод. Для начала посмотрим, как получается аналитическое решения, чтобы увидеть его недостатки. Для этого рассмотрим задачу (1) — (4) и будем искать решение этой задачи в виде
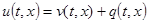 (5)
(5)
где 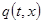 — решение задачи
— решение задачи
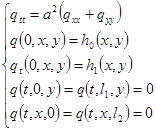 ,(6)
,(6)
а 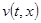 — решение задачи
— решение задачи
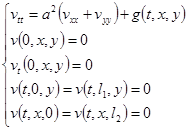 (7)
(7)
Для решения задачи (6) воспользуемся методом Фурье [1], т. е. будем искать (не равное тождественному нулю) частное решение уравнения задачи (6), удовлетворяющее граничным условиям этой задачи, в виде произведения двух функций 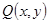 и
и 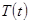 , из которых первая зависит только от
, из которых первая зависит только от 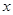 , а вторая только от
, а вторая только от 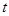 :
:
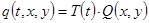 (8)
(8)
В результате мы получим следующую функцию
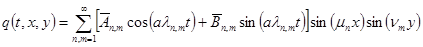 (9)
(9)
где
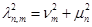 , (10)
, (10)
А параметры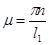 ,
, 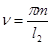 (11)
(11)
Это собственные значения для собчтвенных функций
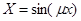 ,
, 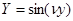 (12)
(12)
Подставляя (9) в начальные условия задачи (6), получаем
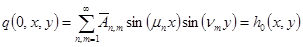 (13)
(13)
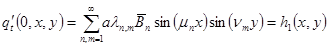 (14)
(14)
Тогда коэффициенты ряда Фурье принимают следующий вид
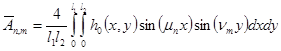 (15)
(15)
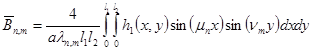 (16)
(16)
Рассмотрим задачу (7). Разложим функцию 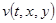 и
и 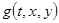 по собственным функциям (12)
по собственным функциям (12)
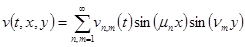 (17)
(17)
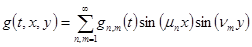 (18)
(18)
Подставляя (17) и (18) в уравнение задачи (7) получим
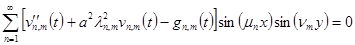 (19)
(19)
Из (19) получаем
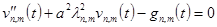 (20)
(20)
После подстановки (17) в начальные условия задачи (7) условия для (20) принимают следующий вид
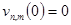 (21)
(21)
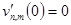 . (22)
. (22)
Решением этой задачи является следующая функция
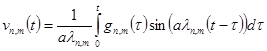 (23)
(23)
Подставив (23) в (17) получим
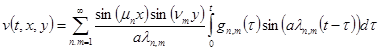 (24)
(24)
где 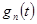 получается из (18) по формуле коэффициентов ряда Фурье [1]
получается из (18) по формуле коэффициентов ряда Фурье [1]
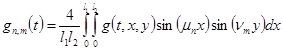 (25)
(25)
А общее аналитическое решение задачи (1) — (4) имеет вид
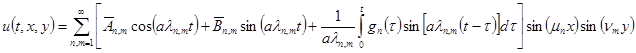 (26)
(26)
Как видно, сам процесс получения аналитического решения довольно нетривиален, даже при условии, что многие этапы я исключил, дабы не нагромождать текст. Любое изменение во входных данных, будь то изменение вида начальных или краевых условий, приводит к необходимости решения задачи практически заново. Для решения задачи (6) мы применяем известный метод математической физики решения таких задач — метод Фурье [1]. Делается предположение, что функцию 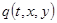 можно представить в виде произведения двух функций
можно представить в виде произведения двух функций 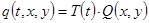 . Но, делая такое предположение, мы теряем тот класс функций, который не может быть приведён к такому виду, т. е. не может быть представлен в терминах концептуального и инструментального аппарата, предлагаемого методом Фурье [1]. То же самое происходит и при решении задачи (7). Также стоит учитывать сложность вычисления интегралов, поскольку заранее мы не знаем исчерпывающе, каковы будут ни функции начальных условий, ни функция
. Но, делая такое предположение, мы теряем тот класс функций, который не может быть приведён к такому виду, т. е. не может быть представлен в терминах концептуального и инструментального аппарата, предлагаемого методом Фурье [1]. То же самое происходит и при решении задачи (7). Также стоит учитывать сложность вычисления интегралов, поскольку заранее мы не знаем исчерпывающе, каковы будут ни функции начальных условий, ни функция 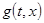 , то есть проще говоря, они могут не браться в квадратурах.
, то есть проще говоря, они могут не браться в квадратурах.
Указанные проблемы не являются единственными, с которыми можно столкнуться при аналитическом решении задачи (1) — (4). Рассмотрим возможность получения численного решения уравнения колебаний прямоугольной мембраны.
Численное решение. Для того чтобы численно решить систему (1) — (4), аппроксимируем её явной конечно-разностной схемой второго порядка аппроксимации [2]. Для этого зададим натуральные числа 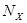 ,
, 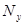 ,
, 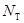 и разобьём рассматриваемую область
и разобьём рассматриваемую область 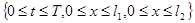 на прямоугольные ячейки параллельными прямыми
на прямоугольные ячейки параллельными прямыми
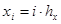 ,
, 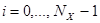 , (27)
, (27)
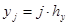 ,
, 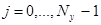 и (28)
и (28)
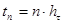 ,
, 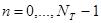 , где (29)
, где (29)
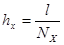 ,
, 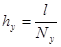 и
и 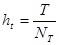 . (30)
. (30)
Конечно-разностная схема будет иметь следующий вид
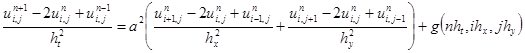 (31)
(31)
Начальное условие (2) и граничное условие (4) примут вид
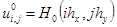 , (32)
, (32)
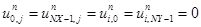 . (33)
. (33)
Для того чтобы аппроксимировать начальное условие (3), введём фиктивный слой
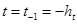 , (34)
, (34)
решение на котором обозначим 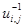 . Аппроксимируем начальное условие (3) со вторым порядком аппроксимации
. Аппроксимируем начальное условие (3) со вторым порядком аппроксимации
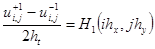 . (35)
. (35)
Используя это можно выразить
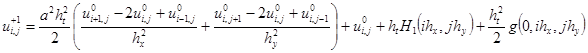 (36)
(36)
В результате конечно-разностная задача и начальные условия имеют второй порядок аппроксимации. Легко показать, что схема (31) устойчива по Нейману [2], для этого рассмотрим однородный вариант уравнения (31) и пусть
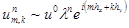 (37)
(37)
Тогда после подстановки можно прийти к следующему выражению — условию устойчивости разностной схемы (31)
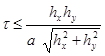 (38)
(38)
Для реализации алгоритма очень удобно воспользоваться языком программирования C++ [3] и библиотекой параллельного программирования OpenMP [5, 6]. Построим схему того, как с помощью библиотеки параллельного программирования OpenMP можно увеличить скорость выполнения программы на многопроцессорных вычислительных машинах. Весь процесс изображён на рисунке 1.
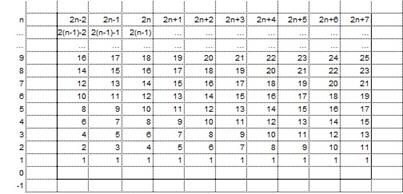
Рис. 1
В самом начале мы определяем значение функции на слое 1 с помощью схемы (36). После этого начиная со второго слоя последовательно проходя по каждому узлу сетки 2, 3, 4, …мы определяем значения функции в этих узлах. Но, уже начиная с 4-го узла, на втором слое мы можем запустить с помощью библиотеки OpenMP параллельный вычислительный поток, который будет работать на третьем слое. Этот узел на третьем слое обозначен как 4, поскольку он запускается в момент запуска 4 узла на втором слое. По достижению на втором слое узла 11 этот вычислительный поток завершается, пока параллельный ему поток на третьем слое продолжает работать. При этом когда в процессе работы на третьем слое поток доходит до узла 6, мы запускаем параллельный вычислительный поток на четвёртом слое и т. д. На рисунки узлы, которые выполняются параллельно, обозначаются одними и теми же цифрами.
Использование так построенного численного алгоритма позволяет сократить время выполнения задачи более чем в 2 раза.
Приведём примеры использования алгоритма численного построения решения уравнения колебаний прямоугольной мембраны на основе схемы (31). В приведённых ниже примерах задавались входные параметры 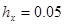 ,
, 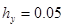 ,
, 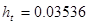 ,
, 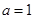 ,
, 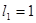 ,
, 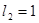 ,
, 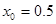 ,
, 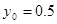 . Графики значений функции
. Графики значений функции 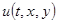 строились в сечении
строились в сечении 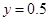 .
.
Пример 1. Рассматривается задача о свободном колебании мембраны с начальными условиями 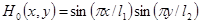 ,
, 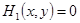 ,
, 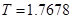 (Решается однородное уравнение (1)). На рис. 2 изображены в разных проекциях свободные колебания прямоугольной мембраны
(Решается однородное уравнение (1)). На рис. 2 изображены в разных проекциях свободные колебания прямоугольной мембраны 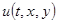
 Рис. 2
Рис. 2
Пример 2. Рассматривается задача о свободном колебании мембраны с другими начальными условиями 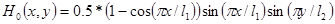 ,
, 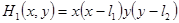 ,
, 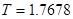 . На рис. 3 изображены в разных проекциях свободные колебания прямоугольной мембраны
. На рис. 3 изображены в разных проекциях свободные колебания прямоугольной мембраны 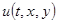
 Рис. 3
Рис. 3
Как можно видеть численный метод решения уравнения колебаний прямоугольной мембраны является очень удобным. Этот способ даёт возможность автоматизации процесса обнаружения и исследования деформационной картины объекта, при этом не зависит от выбранных функций в качестве начальных условий. Всё это и многие другие преимущества могут стать большим подспорьем для дальнейшего исследования и разработки новых методик.
Литература:
1. Тихонов А. Н., Самарский А. А. Уравнения математической физики. — М.: Наука, 1977.
2. Самарский А. А., Гулин А. В. Численные методы. — М.: Наука, 1989.
3. Shieldt G. C++ The complete reference. 3rd edition. — NY.: Osborne McGraw-Hill, 1989.
4. Chapman B., Jost G., Pas R. Using OpenMP. Portable Sharing Memory Parallel Programming. — C.: MIT Press, 2007.
5. Chandra R., Dagum L., Kohr D., Mayden D. Parallel Programming in OpenMP. — NY.: Morgan Kaufmann Publishers, 2008.







