Данная работа является развитием ранее опубликованной статьи «Разработка мультипотоковой модели последовательно связанных информационных элементов» [1]. Здесь мы сделаем ряд уточнений и корректировок, необходимых для успешного применения вышеназванной модели в практических задачах.
Введя ранее понятие информационного элемента i, мы подразумевали его атомарность и неделимость. Информационный поток F, соответственно, является кортежем — упорядоченным конечным набором длины n, каждый из элементов которого in принадлежит некоторому множеству числовых или символьных значений. Информационные элементы в потоке могут повторяться, их повторяемость дает теоретическую возможность прогнозирования поведения потока.
Анализ реальных задач, решение которых предполагается осуществлять с помощью представленной модели, показал, что такое моделирование малопригодно в практическом плане. Можно выделить две проблемы. Первая проблема заключается в том, что при моделировании динамических объектов/явлений мы, как правило, имеем дело с конгломератом параметров, по сути, речь идет о многопараметрических системах. Моделируем ли мы поведение робота или финансовой организации, и в том и в другом случае мы имеем дело с множеством параметров, характеризующих состояние системы в некоторый момент времени. Для робота такими параметрами могут быть его местоположение, заданное в координатах пространства, положение манипуляторов, заряд батареи и др. Для финансовой организации ими могут быть оборотные средства, состояние имущества, привлеченные средства и др.
Очевидно, что если мы моделируем эти объекты совместно с другими, нам необходимо как-то сгруппировать эти параметры, логически обособить одни объекты/явления от других. Таким образом, помимо информационных элементов (которые будут использованы для представления параметров) необходимо еще ввести понятие объединения, которое будет агрегировать параметры, относящиеся к одному и тому же объекту/явлению. Проиллюстрируем это графически (рис. 1).
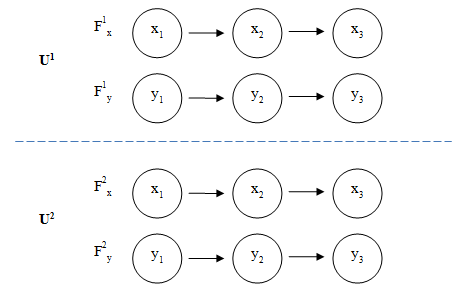
Рис. 1. Объединение родственных потоков
Здесь представлены два объекта, каждый из которых имеет параметры x и y –координаты объекта на плоскости. Соответственно, x1, x2, x3 — значения координаты x в моменты времени t1, t2, t3. F1x — поток информационных элементов, которыми в данном случае являются значения x, верхний индекс 1 означает, что поток относится к 1-му объекту, т. е. это не степень, а идентификатор объекта. Было бы справедливым указать такой же индекс и для значений x (т. е. x11, x12, x12), чтобы подчеркнуть отличие значений x из потоков F1x и F2x. Однако мы не будем этого делать, чтобы не перегружать рисунок, просто следует иметь в виду, что x1 из F1x и x1 из F2x — это разные значения. Аналогичны по смыслу y1, y2, y3 и F1y и F2y, только речь идет о координате y. U1 и U2 — это объединения, агрегирующие информационные элементы и потоки, относящиеся к одному и тому же объекту.
Вторая проблема — это высокая вероятность уникальности информационных элементов. На примере моделирования координат объекта это весьма ожидаемо. Конечно, могут быть случаи моделирования на пространстве малой размерности, но если брать общий случай, то вполне вероятно, что перемещения эти объектов, данные нам в качестве образца (эталонного поведения системы), вообще могут не содержать повторяющихся элементов.
Ранее [1] мы ввели понятие уникальных элементов по отношению к элементам, представленным в потоке, а также сформулировали следующий тезис. «Если все информационные элементы уникальны, то о графе говорить не приходится. Нас интересуют повторяющиеся цепочки, именно они могут быть использованы для задач прогнозирования… Назовем все возможные уникальные элементы словарем, тогда размер словаря (число входящих в него элементов) деленный на число событий в потоке будет характеризовать применимость, полезность данной модели. Отношение равное 1 — это случай неприменимости/бесполезности модели» [1, c. 149].
Таким образом, если руководствоваться этими соображения, то использование данного подхода неэффективно по отношению к прогнозированию перемещений объектов. Прогнозирование потока только лишь на основе повторяемости информационных элементов — это очевидная недоработка, которую нужно исправить. Прежде чем перейти к исправлению, рассмотрим такую ситуацию как сопровождение одного объекта другим. Например, мы хотим смоделировать независимое перемещение объекта № 1 и зависимое объекта № 2. Зависимость будет простой: объект № 2 движется за объектом № 1. В этом случае будет очевидной зависимость координат первого и второго объектов x1 и x2, y1 и y2. Если бы мы накопили опыт перемещений таких объектов, (образец поведения), то легко бы выяснили, что уменьшение или увеличение x1, y1 влияет на соответствующее увеличение или уменьшение x2, y2.
Решение такой задачи в программировании выглядело бы примерно так:
- если x1< x2, то x2 = x2–1 (декремент x2);
- если x1> x2, то x2 = x2 + 1 (инкремент x2);
- если y1< y2, то y2 = y2–1 (декремент y2);
- если y1> y2, то y2 = y2 + 1 (инкремент y2).
Набор таких правил позволяет реализовать алгоритм преследования (или сопровождения) объекта № 1 объектом № 2.
Можно ли реализовать автоматическое построение подобных алгоритмов на основе анализа исходных данных — образцов поведения, т. е. поручить построение такого алгоритма машине≤ Да, конечно. Здесь нет никаких непреодолимых сложностей. Выполняя сравнение однотипных параметров из разных объектов (например, координата x одного объекта сравнивается с координатой x другого объекта), можно найти закономерности. И эту процедуру вполне можно автоматизировать.
Кончено, ситуация значительно усложняется, если речь идет об универсальной системе автоматизированного поиска закономерностей применительно к решению широкого спектра задач. Очевидно, что помимо операций сравнений однотипных параметров: «меньше», «больше», «равно» (операции «меньше» и «больше» применимы к числовым значениям, для символьных они возможны только если заданы правила их сравнения), нам необходимо проверять на равенство параметра некоторой константе. Например, может моделироваться такое поведение, когда преследование осуществляется тогда, когда объект № 1 выходит за некоторую границу (если x1 = k, то начать преследование). Имея повторяющийся опыт пересечения границы объектом № 1 и реагирования на это объекта № 2 (изменения его параметров), машина имеет возможность выявить константные значения границы.
Универсальную схему зависимостей для двух объектов, каждый из которых имеет два параметра, т. е. два потока информационных элементов можно представить следующим образом (рис. 2).
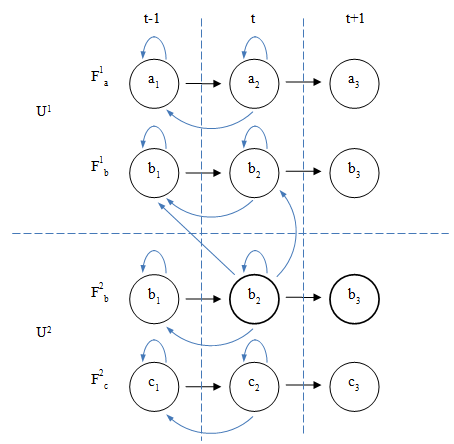
Рис. 2. Универсальная схема зависимостей
Сделаем некоторые пояснения к рисунку. В отличие от предыдущего примера, где оба параметра x и y были однотипными (x1 однотипен по отношению к x2, y1 однотипен по отношению к y2), здесь только один однотипный параметр b. Так как b присутствует в U1 и U2 его можно сравнивать между этим объектами (на что указывают связи между b из разных потоков). Мы не можем сравнивать между собой, например, влажность и температуру, мы можем сравнивать только температуру с температурой, на этом рисунке b и является такой условной температурой, которая характеризует оба объекта.
Параметр также может сравниваться с некоторой величиной, т. е. константой, это сравнение обозначено в виде петли. В более общем случае такое сравнение должно учитывать попадание величины в некоторый диапазон. Если мы будем моделировать поведение человека, то человек, как правило, не измеряет что-то точно, чтобы среагировать на происходящее. Оценка в этом случае происходит приблизительно, «плюс-минус», таким образом, поведение системы будет зависеть от величины, попадающей в некоторый диапазон. И одной из задач автоматизированного поиска зависимостей будет как раз поиск такого диапазон. В случае моделирования точно детерминированных систем поиск диапазона излишен, можно ограничиться поиском константы.
Допустим, что нас интересует связка b2 → b3 из потока F2b. Мы хотим выяснить, при каких условиях происходит переход из b2 в b3, т. е. от чего зависит трансформация b2 в b3. На рисунке 2 представлен опыт системы, т. е. все изменения параметров системы, которые происходили ранее (они уже произошли). Однако сейчас для удобства будем считать, что b2 — это параметр «из настоящего», b1 — «из прошлого», b3 — «из будущего», t — настоящее, t-1 — прошлое, т. е. время предшествующее настоящему, t+1 — будущее системы.
Обладая опытом поведения системы, мы условно знаем будущее, однако пока нам не известно, почему система перешла в это будущее. Почему произошло именно такое изменение: b2 → b3≤ Можно ли выявить причинно-следственные связи изменения данного параметра≤ Ответ на этот вопрос будет утвердительным только в том, случае если мы имеет достаточно полное описание системы. Если зафиксированы именно те параметры, которые влияют на поведение зависимого объекта, тогда мы сможем найти причинно-следственные связи, если описание неполное и важные параметры не отражены, тогда такое моделирование не имеет смысла.
Будем считать, что мы имеем полное описание системы, все параметры, влияющие на изменение b2 из потока F2b, отражены в нашей модели. Теперь нам необходимо выявить зависимость b2 от других информационных элементов. Наверное, самый постой случай зависимости — детерминированный переход из b2 в b3, независимый от других информационных элементов. В данном случае нам нужно проверить равняется ли b2 некоторой константе≤ Или b2 попадает в некоторый диапазон значений, если речь идет о моделировании нечетких систем. Каким образом можно найти эту константу≤ Для этого необходимо в F2b найти все случаи восхождения b3 и для каждого из вхождений определить информационный элемент предшествующий b3. Если это один и тот же элемент b2, тогда мы можем сделать вывод о том, что во всех случаях, когда встречается b2 (в потоке F2b) система обязательно перейдет в b3.
В общем случае попадание в b3 также может детерминировано от любого информационного элемента относящегося к t, а также t-1: a1, a2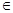 F1a; b1, b2
F1a; b1, b2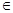 F1b; b1, b2
F1b; b1, b2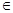 F2b; c1, c2
F2b; c1, c2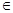 F2c. Зависеть от элементов из t+1 он не может по понятной причине: это будущее, оно еще не наступило и не может влиять на переход системы в b3. Влиять на переход в b3 может только настоящее и прошлое, то, что происходит в данный момент и то, что уже происходило ранее. Влияние информационных элементов t-1, а в общем случае и t-2, t-3, …, t-n — это случаи запаздывающего реагирования.
F2c. Зависеть от элементов из t+1 он не может по понятной причине: это будущее, оно еще не наступило и не может влиять на переход системы в b3. Влиять на переход в b3 может только настоящее и прошлое, то, что происходит в данный момент и то, что уже происходило ранее. Влияние информационных элементов t-1, а в общем случае и t-2, t-3, …, t-n — это случаи запаздывающего реагирования.
Рассмотрим ситуацию запаздывающего реагирования на простом примере. Пусть робот взял манипулятором какой-то объект, затем он переместился из одного местоположения в другое и попал в ситуацию, в которой ему пришлось принимать решение о захвате манипулятором другого объекта. Так как манипулятор уже занят, взять другой объект он не может. Будем считать это опытом системы, образцом ее поведения. Если мы будем моделировать принятие решение о том, использовать ли манипулятор для захвата объекта (это относится к t+1), то очевидно, что нам необходимо учесть факта наличия захвата в прошлом (t-1), состоявшееся перемещение (t) в данном случае никак не влияет на решение.
Переход b2 → b3 может быть детерминирован цепочками информационных элементов, т. е. последовательности определённых значений параметров могут вызвать переход в некоторое состояние. В этом случае необходимо проверять сразу несколько информационных элементов, расположенных последовательно в одном потоке на равенство некоторым константам. Например, цепочка b1 → b2 (b1, b2 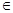 F2b) привела к переходу в b3 (также входящему в F2b). Причиной b3 могла стать и цепочка a1 → a2 (a1, a2
F2b) привела к переходу в b3 (также входящему в F2b). Причиной b3 могла стать и цепочка a1 → a2 (a1, a2 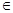 F1a).
F1a).
Зависимость перехода из b2 и b3 может быть обусловлена совокупностью факторов, т. е. свой вклад в b2 → b3 могут вносить сразу несколько типов зависимостей: единичные (равенство одного или нескольких информационных элементов константе); единичные в виде цепочек, относительные (сравнение однотипных элементов из разных объектов).
Все это, конечно, значительно усложняет алгоритмизацию автоматизированного поиска зависимостей, но не делает ее совсем уж невозможной. Дальнейшие исследования будут посвящены уточнению и детализации особенностей такого поиска. Кроме того, нужно учитывать вычислительную сложность при анализе зависимостей для t-n, где n отлично от единицы. Чем дальше в прошлое мы заглядываем, тем больше параметров нам необходимо анализировать. Очевидно, что здесь необходимы методы оптимизации, иначе перебор всех информационных элементов может занять слишком много времени. Пока на этапе теоритических изысканий проблема нехватки вычислительных ресурсов не является актуальной, но в будущем, в процессе прикладных исследований к ней неизбежно придется вернуться.
Литература:
1. Чугреев, В. Л. Разработка мультипотоковой модели последовательно связанных информационных элементов [Текст] / В. Л. Чугреев // Молодой ученый. — 2013. — № 3. — С. 147–149.
2. Чугреев В. Л., Модель структурного представления текстовой информации и метод ее тематического анализа на основе частотно-контекстной классификации: диссертация на соискание уч. ст. к.т.н. — СПб.: СПбГЭТУ «ЛЭТИ», 2003. — 185 с.







