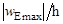Нахождение условий гарантированного разрушения оболочечных конструкций является актуальной научно-технической проблемой при проектировании взрывозащитных инженерных сооружений, при определении технических условий специальных складов боеприпасов и др. Важно определить форму и величину заряда взрывчатого вещества (ВВ), при взрыве которого на некотором расстоянии от оболочечной конструкции, гарантированно произойдет её разрушение. Под разрушением понимаем потерю несущей способности оболочки вследствие появления в ней трещин, сколов, разделений на фрагменты.
Целью настоящей статьи является анализ подходов, примененных для решения вышеописанной задачи о гарантированном разрушении, а именно: энергетического метода [1], предложенного академиком Т. М. Саламахиным, и метода Б. Г. Галеркина [2].
Физическая модель (основные допущения)
Рассмотрим задачу о нахождении необходимой массы С заряда ВВ для гарантированного разрушения открытой цилиндрической оболочки (рисунок 1).
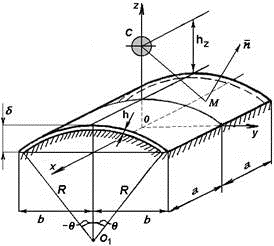
Рис. 1. Схема расположения заряда ВВ над оболочкой при взрыве
Оболочка, с размером плана 2а×2b, выполнена из упругого материала (серый чугун марки СЧ 12–28), имеет постоянную толщину h, радиус кривизны R и защемлена по всему своему контуру в идеальных (недеформируемых) опорах. Оболочка принимается тонкой и пологой, т. е. 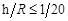 [3] и
[3] и 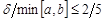 [8] соответственно. Материал оболочки предполагается однородным и изотропным. Рассматривается упругий режим деформирования вплоть до ее разрушения. Принимаются основные классические гипотезы теории тонких оболочек [3]. Прогибы оболочки предполагаются малыми, т. е. не превышающими 1/5 ее толщины. На расстоянии hZот срединного слоя оболочки, над центром симметрии плана, располагается сосредоточенный сферический заряд ВВ радиуса r0, тип и энергетические характеристики которого определяются обобщенным параметром А0.
[8] соответственно. Материал оболочки предполагается однородным и изотропным. Рассматривается упругий режим деформирования вплоть до ее разрушения. Принимаются основные классические гипотезы теории тонких оболочек [3]. Прогибы оболочки предполагаются малыми, т. е. не превышающими 1/5 ее толщины. На расстоянии hZот срединного слоя оболочки, над центром симметрии плана, располагается сосредоточенный сферический заряд ВВ радиуса r0, тип и энергетические характеристики которого определяются обобщенным параметром А0.
В качестве ВВ рассматривается литой тротил с плотностью ρ0 = 1630 кг/м3 и А0 = 400 м/с [4]. Рассматривается ближняя область действия взрыва 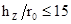 [4], для которой давлением окружающей среды можно пренебречь по сравнению с давлением продуктов взрыва. Вследствие кратковременности действия взрывной нагрузки (время её действия не превышает 2×10–4 с) начальными смещениями точек оболочки, за время действия нагрузки, можно пренебречь [7].
[4], для которой давлением окружающей среды можно пренебречь по сравнению с давлением продуктов взрыва. Вследствие кратковременности действия взрывной нагрузки (время её действия не превышает 2×10–4 с) начальными смещениями точек оболочки, за время действия нагрузки, можно пренебречь [7].
Математическая модель и решение задачи
Введем прямоугольную декартову систему координат Oxyz с началом в центре симметрии плана оболочки (рисунок 1). Обозначим δ — стрелу подъема оболочки над планом, 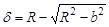 , О1 — центр кривизны, 2θ — угол, определяющий длину дуги цилиндрической оболочки радиуса R.
, О1 — центр кривизны, 2θ — угол, определяющий длину дуги цилиндрической оболочки радиуса R.
Геометрические и механические параметры оболочки: a = 1 м, b = 0.75 м, R = 2 м, h = 4·10–2 м, δ = 0.146м, плотность чугуна ρ = 7.2·103 кг/м3, коэффициент Пуассона μ = 0.25, модуль Юнга Е = 1.2·1011 Па, цилиндрическая жесткость D = Eh3/ [12(1-µ2)], коэффициент однородности на гарантированное разрушение К0* = 1.4, коэффициент динамичности µ3 = 1.3, предел прочности на одноосное растяжение σ р = 1.2·108 Па и на сжатие σ с = 5·108 Па.
Расстояния hZ = {0.2, 0.3, 0.4, 0.5} м. Граничные условия соответствуют способу закрепления оболочки — отсутствию по всему контуру прогибов и углов поперечных поворотов сечений:
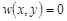 ,
, 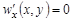 , при x = ± a, (1)
, при x = ± a, (1)
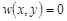 ,
, 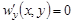 , при y = ± b. (2)
, при y = ± b. (2)
Координатные функции, удовлетворяющие граничным условиям (1) и (2), возьмем в следующем виде
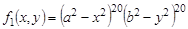 ,
, 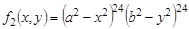 . (3)
. (3)
При относительных расстояниях 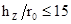 удельный импульс i, действующий на оболочку, может быть вычислен, согласно исследованиям Т. М. Саламахина [4, 7], по формуле
удельный импульс i, действующий на оболочку, может быть вычислен, согласно исследованиям Т. М. Саламахина [4, 7], по формуле
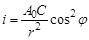 , (4)
, (4)
где r — расстояние от точки М до центра заряда ВВ, φ — угол падения (угол образованный скоростью потока продуктов взрыва с нормалью к поверхности преграды).
Перейдем к решению поставленной задачи энергетическим методом Т. М. Саламахина. Перемещения точек срединной поверхности оболочки с учетом (3), имеют вид [1]:
u (x, y) = 0, v (x, y) = 0, wE (x, y) = c1·f1(x, y) + c2·f2(x, y).
Отметим, что константа c1, входящая в выражение для wE (x, y), предполагается неварьируемой.
Кинетическая энергия Э (приобретенная всей оболочкой за время действия взрывной нагрузки), исходя из (4), и работа ее деформирования П соответственно равны [1]:
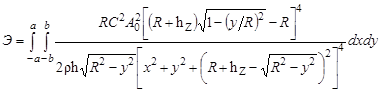 , (5)
, (5)
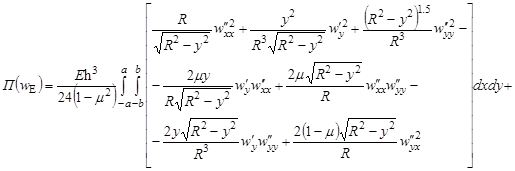 (6)
(6)
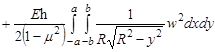 .
.
Применив принцип минимума потенциальной энергии для (6)
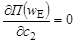
получим, что c2= — 9.326·c1. Для определения c1 воспользуемся критерием разрушения, предложенным П. П. Баландиным [9], в котором учтем динамический характер действующей нагрузки. Согласно введенным основным гипотезам теории тонких оболочек и динамике внешнего воздействия, этот критерий приводит к соотношению
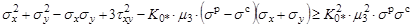 , (7)
, (7)
где, согласно принятым допущениям, для срединной поверхности имеем [1]:
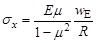 ,
, 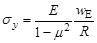 ,
, 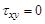 .
.
Равенство в (7) соответствует пересечению поверхности, определяемой левой частью неравенства (7), плоскостью, определяемой правой частью того же неравенства. Это достигается при c1 = 3220. Линии уровня, определяемые критерием разрушения (7), для срединного слоя при найденном c1 показаны на рисунке 2А.
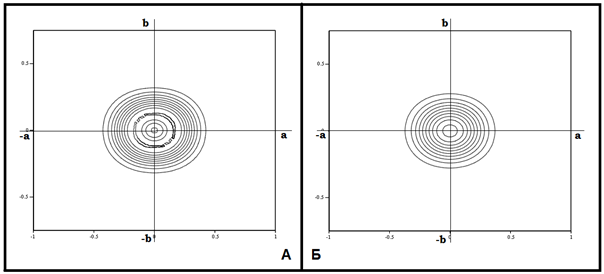
Рис. 2. Линии уровня
Для определения зависимости массы заряда ВВ С от высоты его (заряда) расположения hZ воспользуемся, согласно энергетическому методу Т. М. Саламахина [4–7], соотношением
Э = П,
где Э и П определяются выражениями (5) и (6) соответственно. Результаты вычислений проведены в конце статьи в таблице 1 (масса ВВ обозначается как CE).
Исходя из того, что c1 = 3220 найдем максимальный прогиб wЕmax оболочки. Отношение максимального прогиба к толщине рассматриваемой оболочки будет равно 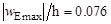 . Данная величина не превышает 1/5 толщины оболочки h, что соответствует введенной гипотезе малых прогибов.
. Данная величина не превышает 1/5 толщины оболочки h, что соответствует введенной гипотезе малых прогибов.
Перейдем к решению задачи методом Б. Г. Галеркина. Согласно принятым допущениям, деформирование оболочки происходит уже после действия взрывной (импульсной) нагрузки, в течение свободных колебаний, которые описываются уравнением
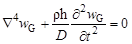 , (8)
, (8)
где wG = wG (x, y, t) — прогиб произвольной точки M(x, y). Начальные условия для уравнения (8) имеют вид:
wG (x, y, 0) = 0, (9)
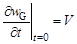 . (10)
. (10)
Начальные скорости точек оболочки V = i/ρh, с учетом (4), выразятся в виде
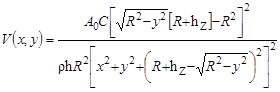 . (11)
. (11)
Функцию прогибов wG (x, y, t), удовлетворяющую граничным условиям (1) и (2), будем искать в виде
wG (x, y, t) = c1(t)·f1(x, y) + c2(t)·f2(x, y). (12)
Начальное условие (9) выполняется, если с1(0) = 0 и с2(0) = 0. Обозначим 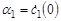 и
и 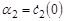 . Зафиксируем высоту hZ = 0.2 м. Найдем из (12) выражение
. Зафиксируем высоту hZ = 0.2 м. Найдем из (12) выражение 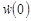 и подставим его в начальное условие (10). Получим невязку F, минимизируя которую аналогично работе [2], придем к соотношениям
и подставим его в начальное условие (10). Получим невязку F, минимизируя которую аналогично работе [2], придем к соотношениям
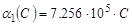 ,
, 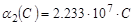 .
.
Таким образом, полностью находим начальные условия для уравнения (8). Подставляя (12) в (8), так же получаем невязку N(x, y, t). Помножив N(x, y, t) на координатные функции f1(x, y), f2(x, y) и проинтегрировав полученные выражение по площади плана оболочки [10], придем к системе уравнений [2], разрешая которые найдем выражения для с1(t) и с2(t). Первое амплитудное колебание происходит в момент времени t* = 0.000613 c.
Напряжения, используемые в критерии разрушения (7), имеют вид
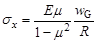 ,
, 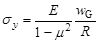 ,
, 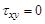 .
.
Равенство в (7) соответствует пересечению поверхности, определяемой левой частью неравенства (7), плоскостью, определяемой правой частью того же неравенства. Это достигается при массе заряда ВВ С = 0.428 кг. Линии уровня, определяемые критерием разрушения (7), для срединного слоя при найденных С и t* показаны на рисунке 2Б.
Сравнение скорости V(x, y) из (11), при массе С = 0.428 кг, со скоростью 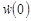 приведено на рисунке 3. Отношение максимального прогиба к толщине оболочки, в момент времени t*, будет равно
приведено на рисунке 3. Отношение максимального прогиба к толщине оболочки, в момент времени t*, будет равно 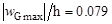 . Данная величина не превышает 1/5, что соответствует введенной гипотезе малых прогибов.
. Данная величина не превышает 1/5, что соответствует введенной гипотезе малых прогибов.
Массы ВВ, времена t*, отношения 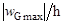 соответствующие высотам hZ = {0.3, 0.4, 0.5} м находим аналогичным способом. Результаты данных вычислений приведены в таблице 1.
соответствующие высотам hZ = {0.3, 0.4, 0.5} м находим аналогичным способом. Результаты данных вычислений приведены в таблице 1.
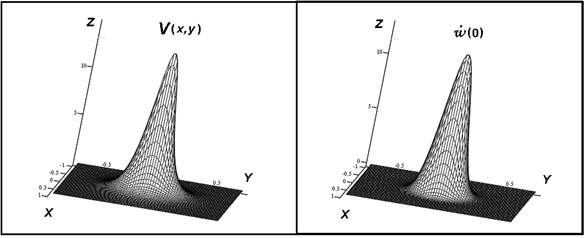
Рис. 3. Сравнение скоростей V(x, y) и 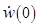
Введем также вспомогательную величину η, характеризующую отклонения между найденными разными способами массами зарядов ВВ
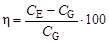 %.
%.
Результаты вычислений для η приведены в таблице 1.
Таблица 1
Сравнение методов решения задачи
|
hZ = 0.2 м |
hZ = 0.3 м |
hZ = 0.4 м |
hZ = 0.5 м |
|
|
СE, кг |
0.578 |
0.886 |
1.205 |
1.538 |
|
СG, кг |
0.428 |
0.694 |
0.995 |
1.335 |
|
η, % |
35.05 |
27.67 |
21.11 |
15.21 |
|
t*, с |
0.000613 |
0.0005648 |
0.0004716 |
0.0004455 |
|
|
0.076 |
0.076 |
0.076 |
0.076 |
|
|
0.079 |
0.078 |
0.078 |
0.079 |
Таким образом, на основании полученных результатов, отраженных в таблице 1, можно говорить о том, что энергетический метод академика Т. М. Саламахина дает завышенные значения по массе заряда ВВ, необходимого для гарантированного разрушения оболочечной конструкции, по сравнению с решением, основанным на методе Б. Г. Галеркина. Это, по мнению авторов, происходит из-за не учета инерционной составляющей в энергетическом методе. Также видно, что разница между массами зарядов ВВ, полученных разными методами для одной высоты hZ, уменьшается с увеличением расстояния от заряда ВВ до оболочечной конструкции.
Литература:
1. Володин Г. Т., Новиков А. С. Разрушение открытой цилиндрической оболочки взрывом неконтактных зарядов конденсированных взрывчатых веществ // Известия Тульского государственного университета. Естественные науки. Вып. 1. — 2013. — С. 75–84.
2. Володин Г. Т., Новиков А. С. Метод Б. Г. Галеркина в задачах гарантированного разрушения оболочечных конструкций взрывом // Materiály IX mezinárodní védecko-praktická conference «Aplikované védecké novinky — 2013». Díl 12. Praha: Publishing House «Education and Science» s.r.o, 2013. — p. 28–35.
3. Новожилов В. В. Теория тонких оболочек. Л.: ГСИСП, 1962. — 432 с.
4. Саламахин Т. М. Физические основы механического действия взрыва и методы определения взрывных нагрузок. М.: ВИА, 1974. — 255 с.
5. Володин Г. Т. Действие взрыва зарядов конденсированных ВВ в газовой и жидкой средах. Часть 2. Взрывостойкость и гарантированное разрушение элементов конструкций. Тула: Левша, 2005. — 160 с.
6. Володин Г. Т. Прямой вариационный метод исследования взрывостойкости и гарантированного разрушения балочных конструкций взрывной нагрузкой // Вестник Тульского государственного университета. Серия Дифференциальные уравнения и прикладные задачи. Вып. 1. — 2009. — С. 49–54.
7. Саламахин Т. М. Разрушение взрывом элементов конструкций. М.: ВИА, 1961. — 275 с.
8. Колкунов Н. В. Основы расчета упругих оболочек. М.: Высшая школа, 1963. — 278 с.
9. Гольденблат И. И., Копнов В. А. Критерии прочности и пластичности конструкционных материалов. М.: Машиностроение, 1968. — 191 с.
10. Флетчер К. Численные методы на основе метода Галеркина. М.: Мир, 1988. — 347 с.