Для некоторых случаев в задачах военного дела дифференциальные игры, описывающиеся с помощью дифференциальных уравнений, играют особо важную роль. Это справедливо, например, для большинства моделей, включающих преследование, отступление и другие элементы маневра. Так, для управления автоматизированными сетями связи в условиях сложной радиоэлектронной обстановки были предприняты попытки использовать стохастические многошаговые антагонистические игры. В данном случае целесообразнее было бы использование дифференциальных игр, т. к. их применение позволяет с большой достоверностью описать необходимые процессы и найти оптимальное решение поставленной задачи.
История возникновения оптимизационных задач исследования операций уходит корнями, как уже говорилось, в далекое прошлое. Еще в конце XIX века известный ученый Ф.Тейлор пришел к выводу о возможности применения научного анализа в сфере производства. Проблема, рассмотренная им, кажется несложной. Как оптимальным образом организовать работу рабочих-землекопов≤ Казалось бы, ответ давно известен — «Бери больше, кидай дальше, отдыхай, пока летит». Однако применение математического аппарата показало несостоятельность этого принципа. Выяснилось, что при разумной экономии рабочей силы оптимальный вес груза, позволяющий увеличивать количество перебрасываемого материала, значительно меньше того, что может поднять человек при максимальной нагрузке.
В годы второй мировой войны исследование операций также применялось при планировании боевых действий. Такие специалисты работали в командовании бомбардировочной авиации США, дислоцированном в Англии. Ими изучались различные факторы, влияющие на эффективность бомбометания. В результате были выработаны определенные стратегии, приведшие к четырехкратному повышению эффективности бомбометания.
В начале войны боевое патрулирование самолетов союзников для обнаружения кораблей и подводных лодок противника носило неорганизованный характер. Привлечение к командованию специалистов по исследованию операций позволило установить такие маршруты патрулирования и такое расписание полетов, при которых вероятность оставить объект незамеченным была сведена до минимума. Полученные рекомендации были применены для организации патрулирования над Южной частью Атлантического океана с целью перехвата немецких кораблей с военными материалами. Из пяти вражеских кораблей, прорвавших блокаду, три были перехвачены на пути из Японии в Германию, один был обнаружен и уничтожен в Бискайском заливе, и лишь одному удалось скрыться благодаря тщательной маскировке. Несмотря на значительные достижения, в теории игр остается еще немало проблем.
В практической деятельности весьма часто приходится рассматривать явления и ситуации, в которых участвуют две (или более) стороны,, имеющие различные интересы и обладающие возможностями применять для достижения своих целей разнообразные действия. Подобные явления и ситуации принято называть конфликтными, или просто конфликтами.
Типичный конфликт характеризуется тремя основными составляющими: заинтересованными сторонами; интересами этих сторон и их возможными действиями. Поэтому для того, чтобы анализ конфликтной ситуации оказался возможным, необходимо пренебречь второстепенными факторами, что при удачном стечении обстоятельств позволяет построить упрощенную формализованную модель конфликта (см. [2, с.17]).Необходимость изучения и анализа конфликтов, представляемых в виде упрощённых математических моделей (игр), вызвала к жизни специальный математический аппарат — теорию игр. С помощью процедуры «Поиск решений» MS EXCEL и встроенных логических функций решение таких матричных задач можно автоматизировать, упростив их решение (см. [3, с.97]).
Иногда в конфликтных ситуациях для достижения лучших результатов противоборствующие стороны объединяются в коалиции. Поэтому возникает необходимость изучения коалиционных дифференциальных игр. Кроме того, идеальных ситуаций (без каких-либо помех, препятствий, посторонних возмущений) в мире не существует. Следовательно, можно исследовать коалиционные дифференциальные игры и при неопределенности. Существуют различные подходы к построению решений дифференциальных игр. Многие военно-тактические задачи не рассматривались с научно-исследовательской точки зрения, хотя имеющийся математический аппарат в принципе позволяет это сделать. Линейные дифференциальные игры составляют частный случай, однако и для них результаты не являются тривиальными. Кроме того, эти результаты более эффективны, чем соответствующие обобщения для нелинейного случая. Математические модели, описываемые с использованиемдифференциальных игр, как показано в [1, с.196], возникают в результате математической идеализации технических задач. При выборе таких идеализаций необходимо стремиться к тому, чтобы, она отражала наиболее существенные черты технической проблемы. В то же время она должна быть доступна для математической обработки. Таким образом, постановка задачи не должна даваться в сильном отрыве от технических проблем.
Рассмотрим конкретный пример модели преследования. Предположим, что один самолет преследует другой. Цель первого самолета догнать второй, цель второго — уйти от преследования. Каждый пилот управляет своим самолетом за своей целью и пользуясь информацией о ситуации. Информация состоит из двух частей, первая — это полное знание технических возможностей обоих самолетов, вторая — это сведения о поведении собственного самолета и самолета противника. Сведения о поведении самолетов могут включать в себя различные данные об их состоянии за период, предшествующий данному моменту, но ничего нельзя считать известным о будущем поведении самолетов, так как они управляемы и в любой момент времени летчик может изменить положение рулей, изменив тем самым поведение самолета. В действительности каждый из пилотов может получать сведения о противнике лишь с некоторым запозданием.
Перейдем к математическому описанию модели преследования. В этом процессе участвуют два управляемых объекта: преследующий объект и убегающий объект. Состояние каждого из объектов в любой момент времени определяется его фазовым вектором. Фазовый вектор преследователя обозначим через x, а убегающего — через y. Тогда уравнения управляемых объектов можно записать в виде:
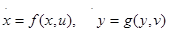, (1)
где точкой обозначили производную по времени, а u и v — управления. Каждый из параметров принадлежит своему ограничивающему множеству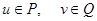 
, где P и Q — множества произвольной природы. Если управление u становится заданной функцией времени t, т. е. u = u(t), то первое из уравнений (1) будет обычным дифференциальным уравнением, которое можно решать при заданном начальном значении 
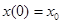. Аналогичные рассуждения справедливы и для второго уравнения из (1).
Упомянутая ранее первая часть информации состоит из уравнений (2). Эти уравнения дают не сами движения объектов, а описывают лишь их возможности, так как при различных управлениях u = u(t) и v = v(t) мы получаем различные движения. Таким образом, в примере с самолетами уравнения (2) описывают технические возможности самолетов. Так как x и y являются фазовыми векторами, то каждый из них распадается на две части
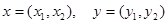, (2)
где 
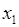и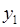 
определяют геометрические положения объектов, а 
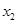и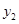 
их скорости. Считается, что процесс преследования заканчивается в тот момент времени, когда наступает равенство 
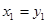, т. е., тогда, когда объекты геометрически совпадают.
Сам процесс преследования мы можем рассматривать с двух различных точек зрения.
1. Рассмотрим игровую ситуацию спозиции преследующего данный объект. В этом случае наша цель заключается в завершении процесса преследования и управление u находится в нашем распоряжении для достижения этой цели. Таким образом, в каждый момент времени t мы должны конструировать значение u(t) управления u, зная уравнения (2), т. е. первую часть информации, и используя вторую ее часть в виде знания функций x(s), y(s), v(s) на отрезке 
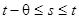, где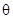 
— некоторым образом выбранное положительное число.
2. Можно рассмотрим игровую ситуацию спозиции убегающего объекта. В этом случае наша цель состоит в предотвращении конца преследования и управление v находится в нашем распоряжении для достижения этой цели. Таким образом, в каждый момент времени t мы должны конструировать значение v(t)управления v, зная уравнения (2), т. е. первую часть информации. Также используется вторая ее часть в виде знания функций x(s), y(s), u(s) на отрезке 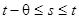. Так проводят математическую идеализацию процесса преследования, которая расщепляет задачу на две различные задачи: задачу преследования и задачу убегания. Расщепление происходит из-за того, что при двух различных подходах мы используем различные информации.
Существует и другая идеализация, при которой, как в задаче преследования, так и в задаче убегания используется одна и та же информация, именно знание значений x(t) и y(t). При этом предполагается, что существует оптимальное управление u = u(x,y) преследования, определяющееся как функция x и y состояний объектов, и существует оптимальное управление v = v(x,y) убегания, определяющееся как функция x и y состояний объектов.
При таком моделировании задача математически становится более определенной. Она заключается в нахождении функций u(x,y) и v(x,y), называемых оптимальными стратегиями. Но именно эта определенность чрезвычайно затрудняет ее решение. В частности, предполагая существование оптимальных стратегий, сужается класс рассматриваемых задач. Дифференциальная игра из процесса преследования возникает в результате естественного стремления упростить обозначения, а именно, вместо двух фазовых векторов x и y мы вводим один вектор: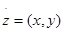 
, образуя фазовое пространство R игры как прямую сумму фазовых пространств обоих объектов. В этом случае пара уравнений (2) записывается в виде одного уравнения
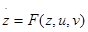. (3)
Военный анализ является более неопределенным в смысле законов, предсказаний и логики, нежели физические науки. Поэтому моделирование с подробно и тщательно подобранными реалистическими деталями не может дать общего достоверного результата, если опыт проведения операции не будет повторен очень большое число раз. Полученные результаты являются более неопределенными в смысле законов, предсказаний и логики и могут иметь вероятностный характер (см. [4, с.27]). С точки зрения дифференциальных игр единственное, на что можно надеяться, — на подтверждение заключений теории. Особенно важны те случаи, когда такие заключения были получены из упрощенной модели.
Литература:
1. Покорная О. Ю. О выборе оптимальных стратегий в планировании боевых операций. Всероссийской научно-практическая конференция «Инновации в авиационных комплексах и системах военного назначения». Воронеж, ВАИУ, Ч.10, 2009, с.194–198.
2. Покорная О. Ю., Покорная И. Ю., Прядкин Д. В. Математическое моделирование оптимальных стратегий в условиях конфликта. Научн. журн.Молодой ученый, 2011. — № 4, Т.1., с. 16–19.
3. Покорная О.Ю Поиск решения как средство решения заджач оптимизации и теории игр. Научн. журн. Молодой ученый, 2012. — № 10, с. 96–98.
4. Покорная О. Ю., Квонг С. В. Интеграл Стильтьеса в теории игр. Научн. журн. Молодой ученый, 2012. — № 3, с. 26–28.
