Анализ состояния фондового рынка на основе многомерных копула-функций на примере акций компании Google

Введение

Целью работы является исследование внутренней зависимости в рядах данных с помощью копула — и автокорреляционных функций.

Термин копула-функция впервые появился в работах W.Hoeffding. Современное понятие копулы было введено A. Sklar. В 2000-х годах копула-функции начинают активно использоваться в микро- и макроэкономике, в связи с этим появляется большое количество научных статей и публикаций на эту тему. Здесь стоит упомянуть книгу Roger B Nelsen (2006), работы Embrechts et al. (2002), Г. И. Пеникаса (2010–2011), Е. М. Бронштейна, Е. И. Прокудиной, А. С. Герасимовой, К. Г. Дубинской (2011).

Краткие сведения

Копула (лат. Copula-пара) — это функция многомерного распределения, определённая на n-мерном единичном кубе [0,1]ⁿ, такая, что каждое её маргинальное распределение равномерно на интервале [0,1].

Определение Функция C(u₁,u₂,...,u_n) от n переменных, определенная на единичном гиперкубе Iⁿ= [0,1]ⁿ (т. е. u_i 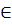 [0,1], i=1,2,…,), называется копула-функцией, если она обладает следующими свойствами:

1)      область значений функции — единичный интервал [0,1];

2)      если u_i =0 по крайней мере для одного i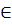{1,2,...,n}, то C(u₁, u₂,..., u_n)=0;

3)      C(1,…,1,u_i,1,...,1) = u_i для любых u_i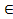 [0,1];

4)      C(u₁, u₂,..., u_n) является n-возрастающей функцией в том смысле, что для всех (a₁,...,a_n), (b₁,...,b_n) 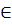 [0,1]ⁿ справедливо неравенство:

,

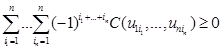где u_j1= a_jи u_j2=b_jдля всех j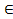{1,…,n}. [2., c. 88]

Связь между совместным распределением случайных величин и копула-функцией выражается следующей теоремой.

Теорема Склара

-        Пусть H(*) — n-мерная функция распределения с частными распределениями F₁(x₁)= P(X≤x₁)…F_n(x_n)= P(X≤x_n). Тогда существует n-мерная копула-функция С такая, что для всех действительных х₁ … х_n:

H(x₁ … x_n)=С(F₁(x₁),…,F_n(x_n)),

причем эта функция будет единственной, если частные функции распределения F₁(x₁)… F_n(x_n)непрерывны. [2, с. 89]

Существуют экстремальные копула-функции, в данной работе были использованы две из них:

1)                  Независимая копула, или копула, или копула произведения, соответствует случаю независимости случайных величин и определяется следующим образом:

С ^┴ (u₁…u_n)=u₁*…*u_n.

2)                  Комонотонная копула соответствует случаю, когда рост одной случайной величины сопровождается ростом других и имеет вид:

C_max(u₁…u_n)=min{u₁…u_n}. [1, c. 220]

Описание исходных данных

Для исследования взяты курсы акций компании Google за 2008–2012 года (брались ежедневные цены закрытия).

Методика исследования

В работе использовалась трехмерная копула-функция. Опишем метод построения её статистической оценки по экспериментальным данным на решетке с шагом 1/N.

Пусть имеются результаты наблюдений 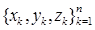, где n — число наблюдений (причем n >> N), x_(i), y_(i)), z_(i)- соответствующие порядковые статистики (вариационные ряды). За оценку значения копула-функции  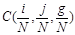принимаем величину n(i,j,g)/n, где n(i,j,g) — число троек выборки 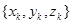, для которых выполняются данные неравенства: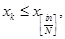  

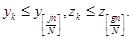
В итоге эмпирическая копула-функция вычисляется следующим образом:

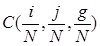=n(i,j,g)/n,

Для каждого временного ряда курсов акций вычисляются оценки значений копула-функции С (u₀, u₁, u₂), где u₀-исходный временной ряд, u₁ и u_2 — временные ряды, сдвинутые относительно исходного на величины t₁ и t₂, находящиеся в промежутке от 1 до 10, причём t₁ < t₂. Затем вычислялись расстояния до эталонной копула-функции C^*, в качестве которой поочередно используются С^┴ иC_max. Расчет производится по формуле:

,

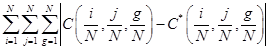где в качестве эталонной копула-функции С* поочередно используются С^┴, C_max.

Результаты исследования

Таблица 1

Суммы отклонений эмпирических от эталонных копула-функций

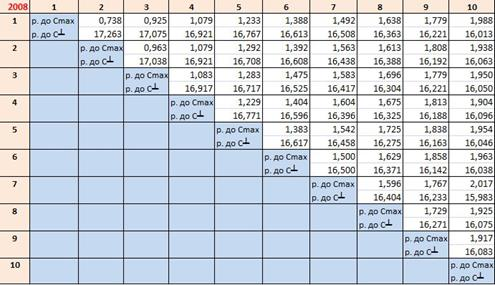
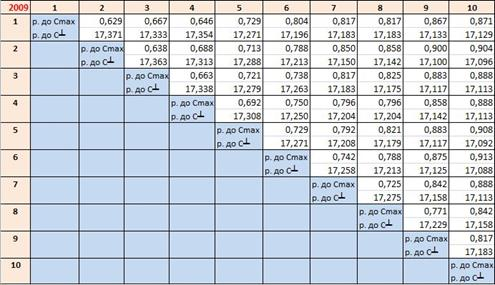
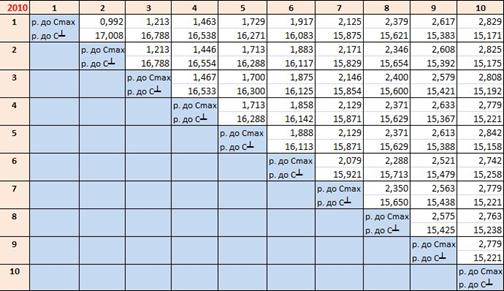
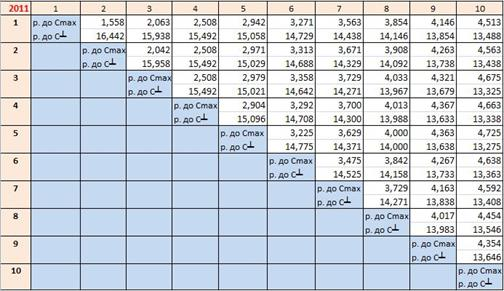
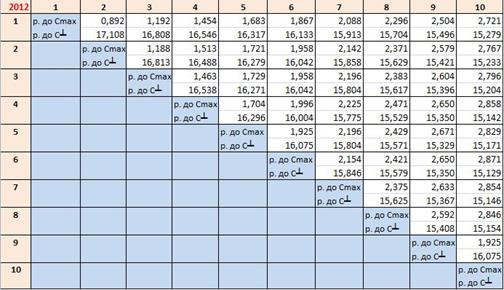
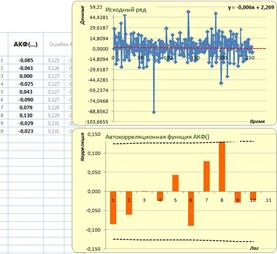
Рис. 1. АКФ за 2008 г.

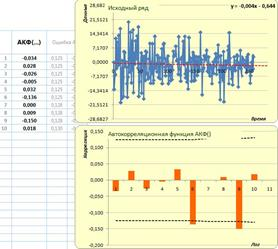
Рис. 2. АКФ за 2009 г.

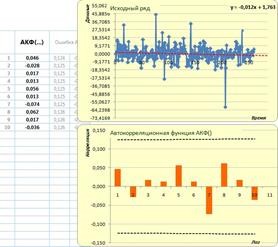
Рис. 3. АКФ за 2010 г.

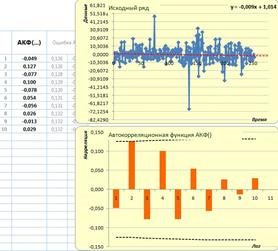
Рис. 4. АКФ за 2011 г.

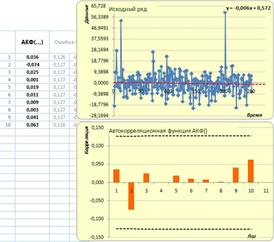
Рис. 5. АКФ за 2012 г.

Интерпретация полученных результатов

По результатам анализа таблицы 1 было обнаружено следующее:

Во-первых, комонотонная связь достаточно сильна, хотя и убывает с увеличением временных лагов.

Во-вторых, расстояния до эталонных копула-функций разные в каждом году. Это можно связать с макроэкономическими факторами, Таблица 2:

Таблица 2

Динамика связей в ряду данных в зависимости от макроэкономического фактора

Отсюда можно сделать вывод о том, что во время экономического подъема во временном ряду усиливается независимость, а во время экономического спада — комонотонная связь.

По результатам анализа построенных автокорреляционных функций можно сделать вывод о том, что, используя АКФ, нельзя дать универсального ответа между какими рядами данных есть зависимость. Как было показано на рисунках 1–5, корреляция была обнаружена только в 2009 году на лагах 6 и 9. Также в основе корреляционного анализа лежит гипотеза о линейной зависимости переменных, в противном случае, коррелограммы показывают отсутствие связи, даже если она там есть. Преимуществом использования многомерных, в частности трехмерных, копула-функций является то, что временной ряд рассматривается сразу в связке с самим собой, сдвинутым на величину лагов, то есть оценивается многомерное распределение, даже если его компоненты, частные функции распределения, и не принадлежат к одному и тому же семейству распределений.

Выводы

В данной работе была произведена оценка характера связи внутри временного ряда в зависимости от величины временных лагов с использованием копула-функций, было выявлено нижеследующее:

Комонотонная связь достаточно сильна, хотя и убывает с увеличением временных лагов.

Во время экономического подъема во временном ряду усиливается независимость, а во время экономического спада — комонотонная связь.

Аппарат копула-функций может быть использован для определения зависимостей между случайными величинами, частные распределения которых принадлежат разным семействам распределений, причем использовать для этого минимальное количество лагов.

Литература:

1.      Е. М. Бронштейн, Е. И. Прокудина, А. С. Герасимова, К. Г. Дубинская (2011). Оценка взаимосвязей временных рядов курсов акций с помощью копула-функций. Журнал «Прикладная эконометрика» № 2(22).

2.      Д.Фантаццини (2011). Моделирование многомерных распределений с использованием копула-функций. Журнал «Прикладная эконометрика» № 2(22).

3.      Nelsen R. (2006). An Introduction to Copulas. N.Y.: Springer.

4.      Г. И. Пеникас (2011). Модели «копула» в задачах хеджирования ценового риска. Журнал «Прикладная эконометрика» № 2(22).

5.      Г. И. Пеникас (2010). Модели «копула» в управлении валютным риском банка. Журнал «Прикладная эконометрика» № 1(17).

6.      Г. И. Пеникас (2010). Модели «копула» в приложении к задачам финансов. Журнал Новой экономической Ассоциации. № 7

7.      http://www.finam.ru

8.      http://stocks.investfunds.ru/

9.      https://www.google.com/finance

10.  http://ru.wikipedia.org/