Актуальной проблемой современной физики атмосферы являются математическое моделирование изменчивости газового и аэрозольного состава атмосферы. Работа посвящена моделированию процессов переноса загрязняющих веществ в воздушной среде с учетом заполненности ячеек. Движение воздушных масс в атмосфере определяется изменением давления воздуха и тепловым режимом. Задачи экологии, по своей природе, не допускают проведения полномасштабных натурных экспериментов, поэтому математическое моделирование является единственным методом для изучения динамики природных катастроф и прогнозирования их последствий, а так же для получения общей картины экологической ситуации. В работе разработана двумерная математическая модель движения воздушной среды, приведены результаты численных экспериментов по моделированию движения воздушной среды и транспорта примесей в воздушной среде.
Ключевые слова: математическое моделирование, воздушная среда, загрязняющие вещества, численный эксперимент.
Количество газообразных и твердых примесей в виде пыли и сажи зависит от характера выбросов в атмосферу, условий разбавления и процессов самоочищения. На концентрацию вредных веществ в атмосфере влияют скорость и направление господствующих ветров, температура, влажность воздуха, осадки, количество, качество и высота выбросов в атмосферу и т. д.
Многие процессы трансформации газовых примесей и аэрозолей протекают в турбулентной атмосфере, поэтому решение задачи о распространении примесей необходимо проводить совместно с гидродинамическими моделями.
Сформулируем основные уравнения, описывающие атмосферные процессы [1, с.75; 2, с. 83; 3, с. 18; 4, с.5–11].
- уравнение неразрывности
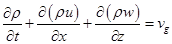, (1)
- уравнение Навье-Стокса
,
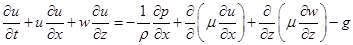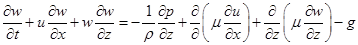, (2)
- уравнение состояния
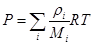, (3)
где g — ускорение свободного падения, р — давление,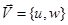 
— компоненты вектора скорости, 
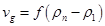— массовая скорость испарении, 
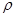— плотность жидкости, m — масса, M — молярная масса, R — универсальная газовая постоянная, V — объем, Т — температура.
Система уравнений (1) — (3) рассматривается при следующих граничных условиях [5, с. 35; 6, с. 10–17; 7, с. 245]:
- на нижней поверхности
;
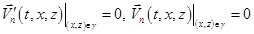- на верхних и боковых границах
;
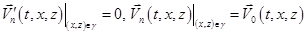где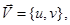 
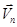— нормальная составляющая вектора скорости, 
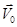— значение вектора скорости на вертикальной и боковых границах расчетной области.
При соприкосновении поверхности жидкости с ее паром при данной температуре устанавливается определенное для каждой жидкости равновесное давление пара. Конденсация пара на поверхности жидкости происходит даже при бесконечно малом увеличении давления пара над этой поверхностью, а испарение жидкости с ее поверхности происходит при бесконечно малом уменьшении давления.
Принимая во внимание, что в атмосфере происходят такие процессы, как конденсация и испарение, а также тот факт, что в процессе транспорта примесей взвешенные частицы осаждаются, опишем процесс переноса загрязняющих веществ следующим уравнением:
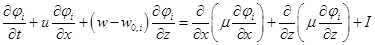, (4)
где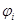 
— объемные доли i-ой фазы (i=0 — воздух, 1 — вода в газообразном состоянии, 2 — газ на источнике, 3 — вода в жидком состоянии, 4 — сажа), I — функция, описывающая распределение и мощность источников примесей, 
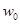— скорость осаждения твердых веществ.
Для аппроксимации модели движения воздушной среды по временной переменной использовался метод поправки к давлению, применены аддитивные двумерно — одномерные разностные схемы, устойчивость которых исследовалась на основе сеточного принципа максимума. Исходная непрерывная задача была преобразована в систему линейных алгебраических уравнений, которая была решена при помощи построенного проблемно–ориентированного программного комплекса. Для решения сеточных уравнений использован адаптивный попеременно-треугольный итерационный метод [8, с. 18–21; 9, с. 335–339; 10, с. 32–44]. На основе построенных алгоритмов был создан комплекс программ, предназначенный для численного моделирования движения воздушной среды и транспорта примесей в многокомпонентной воздушной среде.
На рис. 1–2 приведены результаты численных экспериментов по моделированию движения воздушной среды. Палитрой показано поле давления и концентрация воздушной среды.
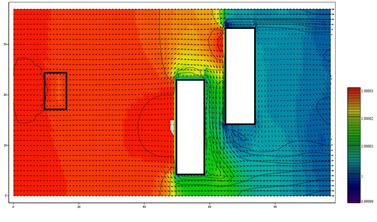
Рис. 1. Поле давления
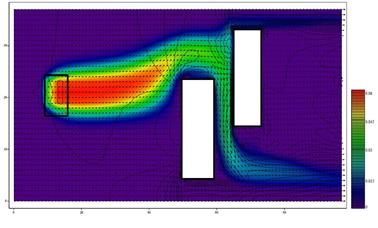
Рис. 2. Концентрация воздушной среды
Прямоугольником, находящимся в левой части расчетной области, показана зона, в которой осуществляются выбросы загрязняющих веществ.
Из рис. 2 видно, что происходит расширение воздушной среды в области выброса загрязняющих веществ. Учет данного эффекта при моделировании движения воздушной среды повышает точность расчетов транспорта загрязняющих веществ.
Выводы. В работе разработана двумерная математическая модель движения воздушной среды, приведены результаты численных экспериментов по моделированию движения воздушной среды и транспорта примесей в воздушной среде, построены картины течений. В работе так же показа эффективность методики построения дискретных математических моделей, учитывающих степень заполенности контрольных ячеек, при решении задач аэродинамики.
Литература:
1. Сухинов А. И., Чистяков А. Е., Хачунц Д. С. Математическое моделирование движения многокомпонентной воздушной среды и транспорта загрязняющих веществ// Известия ЮФУ. Технические науки. –2011. № 8(121). — С 73–79.
2. Сухинов А. И., Хачунц Д. С. Задача движения многокомпонентной воздушной среды с учетом парообразования и конденсации// Известия ЮФУ. Технические науки. –2013. № 4(254). — С 81–86.
3. Чистяков А. Е., Хачунц Д. С. Программная реализация двумерно задачи движения воздушной среды// Известия ЮФУ. Технические науки. –2013. № 4(254). — С 15–21.
4. Сухинов А. И., Чистяков А. Е., Алексеенко Е. В. Численная реализация трехмерной модели гидродинамики для мелководных водоемов на супервычислительной системе// Математическое моделирование. — 2011. — Т.23, № 3, — С. 3–21.
5. Сухинов А. И., Чистяков А. Е., Тимофеева Е. Ф., Шишеня А. В. Математическая модель расчета прибрежных волновых процессов// Математическое моделирование. — 2012. — Т.24, № 8, — С. 32–44.
6. Сухинов А. И., Никитина А. В., Чистяков А. Е. Моделирование сценария биологической реабилитации Азовского моря // Математическое моделирование. — 2012. — Т.24, № 9, — С. 3–21.
7. Чистяков А. Е. Теоретические оценки ускорения и эффективности параллельной реализации ПТМ скорейшего спуска// Известия ЮФУ. Технические науки. — 2010. № 6(107). — С 237–249.
8. Сухинов А. И., Чистяков А. Е. Адаптивный модифицированный попеременно-треугольный итерационный метод для решения сеточных уравнений с несамосопряженным оператором// Математическое моделирование. — 2012. — Т.24, № 1, — С. 3–21.
9. Никитина А. В., Чистяков А. Е., Фоменко Н. А. Применение адаптивного модифицированного попеременно–треугольного итерационного метода для численной реализации двумерной математической модели движения водной среды// Инженерный вестник Дона. — 2012, — Т.20, № 2, — С. 335–339.
10. Сухинов А. И., Чистяков А. Е., Проценко Е. А. Построение дискретной двумерной математической модели транспорта наносов// Известия ЮФУ. Технические науки. — 2011. № 8 (121). — С 32–44.
