В статье представлены методики и математическая модель оценки влияния технического состояния элементов ЭСУД автомобиля на экологические показатели.
Ключевые слова: электронная система управления двигателем, экологические показатели, корреляционно-регрессионные зависимости.
В процессе проведения испытаний осуществляется имитация отказов элементов ЭСУД (датчика массового расхода воздуха — Дмрв; датчика положения дроссельной заслонки — Дпдз; датчика температуры воздуха во впускной системе — Двоз; датчика положения распределительного вала — Дпрв; регулятора добавочного воздуха — РДВ; датчика детонации — Ддет; датчика температуры охлаждающей жидкости — Дтож) с измерением CO, CH, O2, CO2 и λ на режимах работы двигателя [1]. Результаты измерения подлежат, в последующем обработке, с построением корреляционно-регрессионных зависимостей [2], отражающих изменение результирующих параметров (выбросов ОГ) в зависимости от технического состояния элементов ЭСУД, т. е.
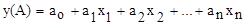 , (1)
, (1)
где a0, a1, a2….an — коэффициенты уравнения регрессии;
x1,x2,….xn- управляемые в процессе эксперимента факторы (независимые переменные, характеризующие техническое состояние элементов ЭСУД).
В данном выражении в качестве множества выходных параметров A выступают:
A = (CO,CH,O2,CO2,λ), (2)
Управляемыми факторами xi 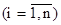 являются переменные вида:
являются переменные вида:
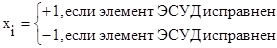 (3)
(3)
При этом множеству факторов {xi} соответствует техническое состояние следующих элементов: x1→Дмрв; x2→Дпдз; x3→Двоз; x4→Дпрв; x5→РДВ; x6→Ддет; x7→ Дтож.
Поскольку нагрузочные испытания проводятся в диапазоне заданных оборотов двигателя nдв и имитаций нагрузок Р на установившемся режиме движения автомобиля, то эти факторы (nдв и Р) выступают в качестве дополнительных при оценке вышеотмеченных результирующих параметров, т.е x8→ nдв; x9→P.
В общем виде необходимые исходные данные, включающие массив переменных  и выходные параметры, получаемые в процессе экспериментальных исследований, представлены в табл.1 и 2. В данных таблицах отражены условия проведения эксперимента для случаев имитации движения автомобиля на установивших режимах (имитация осуществляется путем задания нагрузки и оборотов двигателя на нагрузочном стенде на прямой передаче КПП) и условия эксеримента при работе двигателя на режимах холостого хода для задаваемых оборотов nдв =1000 об/мин и повышенных оборотов nдв =2500 об/мин. (т. е. без имитации движения автомобиля).
и выходные параметры, получаемые в процессе экспериментальных исследований, представлены в табл.1 и 2. В данных таблицах отражены условия проведения эксперимента для случаев имитации движения автомобиля на установивших режимах (имитация осуществляется путем задания нагрузки и оборотов двигателя на нагрузочном стенде на прямой передаче КПП) и условия эксеримента при работе двигателя на режимах холостого хода для задаваемых оборотов nдв =1000 об/мин и повышенных оборотов nдв =2500 об/мин. (т. е. без имитации движения автомобиля).
Проверка многофакторных моделей (1) на адекватность производится по критерию Фишера и средней ошибке аппроксимации [3].
Оценка полученной математической модели производится путем сравнения критерия Фишера F с его табличным значением [F].
Модель считается адекватной, если выполняется условие
F ≥ [F] (4)
или
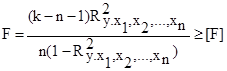 , (5)
, (5)
где k — объем выборки;
n — число независимых факторов модели;
[F] — табличное значение критерия Фишера для заданного уровня значимости и числа степеней свободы (k-n-1);
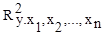 — квадрат множественного коэффициента корреляции.
— квадрат множественного коэффициента корреляции.
Для оценки тесноты связи между результирующим признаком  и независимыми переменными факторами x1,x2,…xn применяется коэффициент множественной корреляции, Ry\.x1,x2,…,xn, позволяющий оценивать влияние совместного действия всех рассматриваемых в модели факторов x1,x2,…xn на результирующий признак y [1]. Его величина определяется из выражения вида:
и независимыми переменными факторами x1,x2,…xn применяется коэффициент множественной корреляции, Ry\.x1,x2,…,xn, позволяющий оценивать влияние совместного действия всех рассматриваемых в модели факторов x1,x2,…xn на результирующий признак y [1]. Его величина определяется из выражения вида:
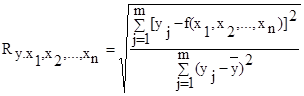 , (6)
, (6)
где yj — экспериментальные значения результирующего признака 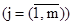 ;
;
f(x1,x2,…,xn) — уравнение множественной регрессии, полученное в результате аналитической обработки исходных данных yj; x1j,x2j,…,xnj;
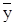 — среднее значение результирующего признака
— среднее значение результирующего признака
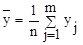 . (7)
. (7)
Единицей измерения одновременного влияния, оказываемого вариациями всех исследуемых факторов, является квадрат множественного коэффициента корреляции или коэффициент множественной детерминации [1].
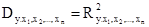 . (8)
. (8)
В процессе построения многофакторных моделей (1) и определения коэффициентов уравнений регрессии ai необходима оценка степеней влияния xi на y, выражаемых через β -коэффициенты [1] т. е.
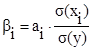 (9)
(9)
В (9) β — коэффициенты показывают на какую долю своей единицы измерения σ(y) изменится показатель y (т. е. CO,CH,O2,CO2,λ), если фактор xi изменится на свою единицу σ(xi) при условии, что все остальные факторы остаются неизменными.
Таким образом, практическая реализация экспериментальных исследований позволит оценить, через коэффициенты 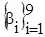 , влияние технического состояния элементов (датчиков) x1,x2,….x7 а также оборотов двигателя x8 и нагрузки x9 на выходные диагностические параметры Aj, т. е. на CO,CH,O2,CO2,λ. Это обеспечит получение оценочных статистических характеристик
, влияние технического состояния элементов (датчиков) x1,x2,….x7 а также оборотов двигателя x8 и нагрузки x9 на выходные диагностические параметры Aj, т. е. на CO,CH,O2,CO2,λ. Это обеспечит получение оценочных статистических характеристик 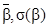 изакономерностей распределений F(βi), выступающих в качестве безусловных вероятностей проявления образов βi для каждого выходного параметра Aj.
изакономерностей распределений F(βi), выступающих в качестве безусловных вероятностей проявления образов βi для каждого выходного параметра Aj.
Таблица 1
Пример представления входных и выходных параметров в процессе проведения эксперимента (имитация движения автомобиля и нагрузки на установившихся режимах)
|
Независимые переменные |
Р, кгс |
Nei, л.с |
Vai, км/ч |
Выходные параметры |
|||||||||||
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
СОi % |
CHi, млн-1 |
O2, % |
СО2i % |
λi |
||
|
1 . 1 |
1 . 1 |
1 . 1 |
1 . 1 |
1 . 1 |
1 . 1 |
1 . 1 |
nдв1 . nдвn |
Р1 . Рn |
Ne1 . Nen |
Va1 . Van |
СО(1) . СО(n) |
CH(1) . CH(n) |
О(1) . О(n) |
СО2(1) . СО2(n) |
λ1 . λn |
|
-1 . –1 |
1 . 1 |
1 . 1 |
1 . 1 |
1 . 1 |
1 . 1 |
1 . 1 |
nдв1 . nдвn |
Р1 . Рn |
Ne1 . Nen |
Va1 . Van |
СО(1) . СО(n) |
CH(1) . CH(n) |
О(1) . О(n) |
СО2(1) . СО2(n) |
λ1 . λn |
|
1 . 1 |
-1 . –1 |
1 . 1 |
1 . 1 |
1 . 1 |
1 . 1 |
1 . 1 |
nдв1 . nдвn |
Р1 . Рn |
Ne1 . Nen |
Va1 . Van |
СО(1) . СО(n) |
CH(1) . CH(n) |
О(1) . О(n) |
СО2(1) . СО2(n) |
λ1 . λn |
|
1 . 1 |
1 . 1 |
-1 . –1 |
1 . 1 |
1 . 1 |
1 . 1 |
1 . 1 |
nдв1 . nдвn |
Р1 . Рn |
Ne1 . Nen |
Va1 . Van |
СО(1) . СО(n) |
CH(1) . CH(n) |
О(1) . О(n) |
СО2(1) . СО2(n) |
λ1 . λn |
|
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
|
1 . 1 |
1 . 1 |
1 . 1 |
1 . 1 |
1 . 1 |
1 . 1 |
-1 . –1 |
nдв1 . nдвn |
Р1 . Рn |
Ne1 . Nen |
Va1 . Van |
СО(1) . СО(n) |
CH(1) . CH(n) |
О(1) . О(n) |
СО2(1) . СО2(n) |
λ1 . λn |
Таблица 2
Пример представления входных и выходных параметров в процессе проведения эксперимента (условия работы двигателя на режимах холостого хода для задаваемых оборотов двигателя nдв =1000 об/мин и повышенных оборотах nдв =2500об/мин).
|
№ п.п |
Независимые переменные |
Выходные параметры |
|||||||||||
|
Дмрв |
Дпдз |
Двоз |
Дпрв |
РДВ |
Ддет |
Дтож |
nдв |
СОi, % |
CHi, млн-1 |
O2, % |
СО2i, % |
λi |
|
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
||||||
|
1 2 |
1 1 |
1 1 |
1 1 |
1 1 |
1 1 |
1 1 |
1 1 |
1000 2500 |
СО(1) СО(2) |
CH(1) CH(2) |
О(1) О(2) |
СО2(1) СО2(2) |
λ1 Λ2 |
|
1 2 |
-1 —1 |
1 1 |
1 1 |
1 1 |
1 1 |
1 1 |
1 1 |
1000 2500 |
СО(1) СО(2) |
CH(1) CH(2) |
О(1) О(2) |
СО2(1) СО2(2) |
λ1 Λ2 |
|
1 2 |
1 1 |
-1 —1 |
1 1 |
1 1 |
1 1 |
1 1 |
1 1 |
1000 2500 |
СО(1) СО(2) |
CH(1) CH(2) |
О(1) О(2) |
СО2(1) СО2(2) |
λ1 Λ2 |
|
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. . |
|
1 2 |
1 1 |
1 1 |
1 1 |
1 1 |
1 1 |
1 1 |
-1 —1 |
1000 2500 |
СО(1) СО(2) |
CH(1) CH(2) |
О(1) О(2) |
СО2(1) СО2(2) |
λ1 Λ2 |
Проведенные предварительные исследования и их экспериментальная реализация позволят, в конечном итоге, подойти к разработке математической модели оценки диагностической ценности выявления технического состояния рассматриваемых элементов, с последующей разработкой рациональных процедур (планов) проверок технического состояния ЭСУД, влияющих на восстановление экологических показателей работы двигателя.
Литература:
1. Нгуен Минь Тиен. Исследование режимов проведения стендовых испытаний электронных систем управления двигателем автомобиля/ Журнал «Молодой ученый»./ М., 11/2013.
2. Вероятностно-статистические методы на автотранспорте. Галушко В. Г. Издательское объединение «Вища школа», 1976, — с.232.
3. Завадский Ю. В. Решение задач автомобильного транспорта и дорожно-строительных машин с помощью регрессионно-кореляционного анализа (Учебн. пособие для слушателей ФПК) — М.: 1981. — 116 с.







