Рассматривается задача получения функционала, который полностью описывают все возможные состояния физического объекта для управления им. Этот функционал называется интегралом энергии. В статье приведены способы получения интеграла энергии на примере прямоугольной мембраны, балки и прямоугольной пластины.
Ключевые слова: прямоугольная мембрана, балка, прямоугольная пластина, колебания системы, управление, интеграл энергии.
Введение. Рассматривая задачи управления какими-либо физическими процессами нельзя не отметить задачи, относящиеся к задачам о гашении колебаний различных физических объектов. Подобного рода задачи имеют огромное прикладное значение поскольку могут позволить управлять различного рода процессами разрушений и дать возможность стабилизировать объект до разрушения. В данной области ведутся исследования, основанные преимущественно на численных методах решения таких задач [1–7]. Но как любая задача управления, гашение колебаний требует объекта управления. И как бы это не звучало парадоксально, управление осуществляется не над самим объектом, а над определённой группировкой его физических свойств, неким функционалом, который описывает все возможные состояния объекта исследования во времени.
В этой работе будет показано, как найти такие функционалы, которые называются интегралами энергии, на примере прямоугольной мембраны, балки и прямоугольной пластины.
Интеграл энергии прямоугольной мембраны. Колебания таких структур как прямоугольные мембраны описываются уравнением общего вида
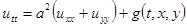 ,
, 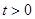 ,
,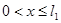 ,
,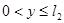 ,
,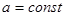 . (1.1)
. (1.1)
Начальные отклонения и скорость перемещения этого первоначального возмущения мембраны
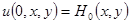 ,
, 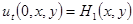 (1.2)
(1.2)
будем рассматривать как начальные условия. На границе прямоугольной мембраны наложим условие закрепления согласно
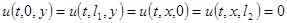 (1.3)
(1.3)
Утверждение. Пусть функция 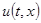 дважды непрерывно дифференцируема в замкнутой области
дважды непрерывно дифференцируема в замкнутой области 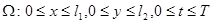 , и является решением задачи
, и является решением задачи
(1.4)
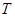 — произвольно фиксированное положительное число. Тогда
— произвольно фиксированное положительное число. Тогда 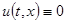 в области
в области 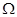 .
.
Доказательство. Умножим уравнение 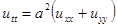 на
на 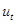 и проинтегрируем по области
и проинтегрируем по области 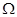 . Получим
. Получим
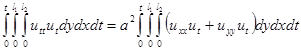 . (1.5)
. (1.5)
Заметим, что
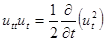 (1.6)
(1.6)
и поэтому
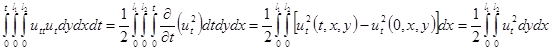 . (1.7)
. (1.7)
Далее, применим два раза интегрирование по частям к первой сумме правой части равенства в уравнении (1.5)
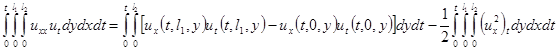
или
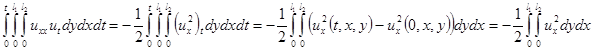 (1.8)
(1.8)
Это равенство (1.8) получилось благодаря тому, что 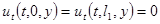 получается из дифференцирования условий
получается из дифференцирования условий 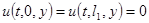 по
по 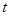 , а
, а 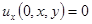 получается, если продифференцировать условие
получается, если продифференцировать условие 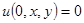 по
по 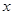 . Далее, применим два раза интегрирование по частям ко второй сумме правой части равенства в уравнении (1.5)
. Далее, применим два раза интегрирование по частям ко второй сумме правой части равенства в уравнении (1.5)
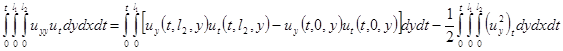 или
или
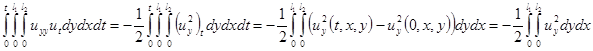 (1.9)
(1.9)
Это равенство (1.9) получилось благодаря тому, что 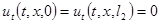 получается из дифференцирования условий
получается из дифференцирования условий 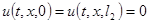 по
по 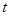 , а
, а 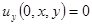 получается, если продифференцировать условие
получается, если продифференцировать условие 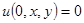 по
по 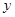 .
.
Следовательно
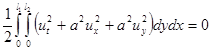 (1.10)
(1.10)
Интеграл
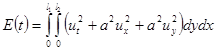 (1.11)
(1.11)
называется интегралом энергии прямоугольной мембраны. Мы видим, что 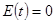 . Далее, из равенства нулю интеграла энергии следует, что
. Далее, из равенства нулю интеграла энергии следует, что 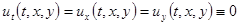 в области
в области 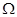 . Значит
. Значит 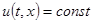 в области
в области 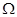 . А так как функция
. А так как функция 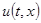 непрерывна в области
непрерывна в области 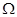 и
и 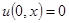 следует, что
следует, что 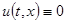 в
в 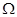 .
.
Интеграл энергии балки. Колебания балки описываются гиперболическим по Петровскому уравнением
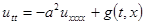 ,
, 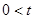 ,
,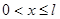 ,
,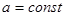 (2.1)
(2.1)
Начальные отклонения и скорость перемещения этого первоначального возмущения балки
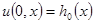 ,
, 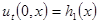 , (2.2)
, (2.2)
будем рассматривать как начальные условия. На концах балки наложим условия нежёсткого (шарнирного) закрепления
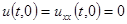 ,
, 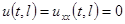 . (2.3)
. (2.3)
Утверждение. Пусть функция 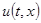 четырежды непрерывно дифференцируема в замкнутой области
четырежды непрерывно дифференцируема в замкнутой области 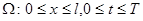 , и является решением задачи
, и является решением задачи
(2.4)
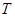 — произвольно фиксированное положительное число. Тогда
— произвольно фиксированное положительное число. Тогда 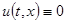 в области
в области 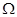 .
.
Доказательство. Умножим уравнение 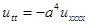 на
на 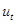 и проинтегрируем по области
и проинтегрируем по области 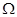 . Получим
. Получим
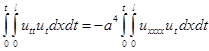 . (2.5)
. (2.5)
Заметим, что
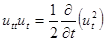 (2.6)
(2.6)
и поэтому
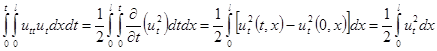 . (2.7)
. (2.7)
Далее, применим два раза интегрирование по частям к правой части равенства в уравнении (2.5)
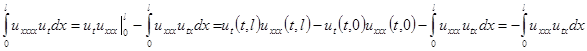 .
.
Это равенство получилось благодаря тому, что 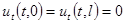 получается из дифференцирования условий
получается из дифференцирования условий 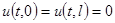 . Далее
. Далее
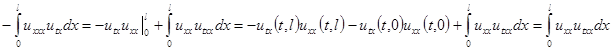 Следовательно
Следовательно
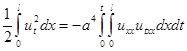 (2.8)
(2.8)
Поскольку 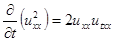 , то (2.8) преобразуется к виду
, то (2.8) преобразуется к виду
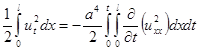 . (2.9)
. (2.9)
Тогда можно записать
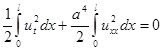 . (2.10)
. (2.10)
Интеграл, полученный из (П2.10)
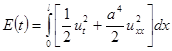 (2.11)
(2.11)
называется интегралом энергии балки. Мы видим, что 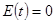 . Далее, из равенства нулю интеграла энергии следует, что
. Далее, из равенства нулю интеграла энергии следует, что 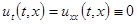 в области
в области 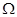 . Значит
. Значит 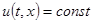 в области
в области 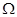 . А так как функция
. А так как функция 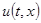 непрерывна в
непрерывна в 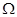 и
и 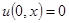 следует, что
следует, что 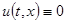 в
в 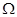 .
.
Интеграл энергии прямоугольной пластины. Колебания Малые поперечные колебания упругой изотропной пластины постоянной толщины описываются уравнением Жармен-Лагранжа
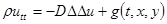 ,
, 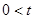 ,
,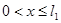 ,
, 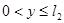 (3.1)
(3.1)
где 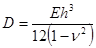 — изгибная жесткость пластинки;
— изгибная жесткость пластинки; 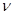 — коэффициент Пуассона;
— коэффициент Пуассона; 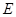 — модуль Юнга;
— модуль Юнга; 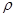 — удельная плотность на единицу площади пластинки;
— удельная плотность на единицу площади пластинки; 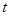 — время. Для большего удобства это уравнение можно привести у виду
— время. Для большего удобства это уравнение можно привести у виду
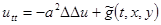 ,
, 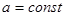 (3.2)
(3.2)
Начальные отклонение и скорость его распространения будем рассматривать как начальные условия
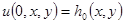 ,
, 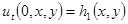 . (3.3)
. (3.3)
На концах пластины наложим условия шарнирного закрепления
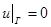 ,
, 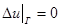 (3.4)
(3.4)
Утверждение. Пусть функция 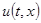 четырежды непрерывно дифференцируема в замкнутой области
четырежды непрерывно дифференцируема в замкнутой области 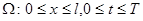 , и является решением задачи
, и является решением задачи
(3.5)
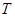 — произвольно фиксированное положительное число. Тогда
— произвольно фиксированное положительное число. Тогда 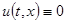 в области
в области 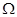 .
.
Доказательство. Умножим уравнение 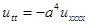 на
на 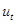 и проинтегрируем по области
и проинтегрируем по области 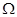 . Получим
. Получим
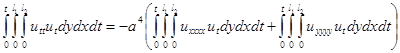 . (3.6)
. (3.6)
Заметим, что
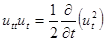 (3.7)
(3.7)
и поэтому
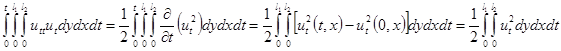 (3.8)
(3.8)
Далее, применим два раза интегрирование по частям к каждому из слагаемых в правой части равенства в уравнении (3.6), при этом рассмотрим интегралы только по той переменной, по которой берётся производная.
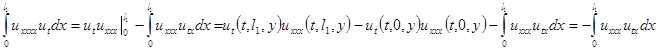 (3.9)
(3.9)
Это равенство получилось благодаря тому, что 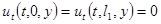 получается из дифференцирования условий
получается из дифференцирования условий 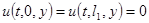 . Далее
. Далее
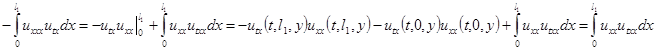 (3.10)
(3.10)
А поскольку 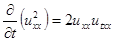 , тогда первое слагаемое в правой части (3.6) можно записать следующим образом
, тогда первое слагаемое в правой части (3.6) можно записать следующим образом
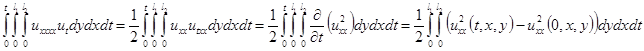 (3.11)
(3.11)
Учитывая, что 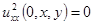 , что в свою очередь получается из дифференцирования начального условия в (3.5), получаем
, что в свою очередь получается из дифференцирования начального условия в (3.5), получаем
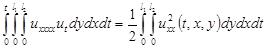 (3.12)
(3.12)
Теперь возьмём второе слагаемой в правой части равенства (3.6) и применим все действия, которые производили выше.
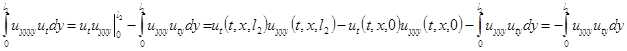 (3.13)
(3.13)
Это равенство получилось благодаря тому, что 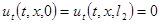 получается из дифференцирования условий
получается из дифференцирования условий 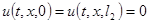 . Далее
. Далее
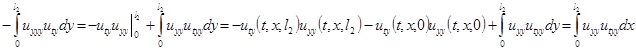 (3.14)
(3.14)
А поскольку 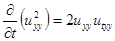 , тогда первое слагаемое в правой части (3.15) можно записать следующим образом
, тогда первое слагаемое в правой части (3.15) можно записать следующим образом
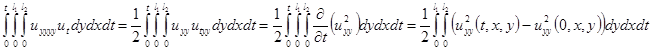 (3.15)
(3.15)
Учитывая, что 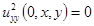 , что в свою очередь получается из дифференцирования начального условия в (3.5), получаем
, что в свою очередь получается из дифференцирования начального условия в (3.5), получаем
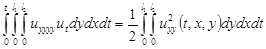 (3.16)
(3.16)
Тогда можно записать
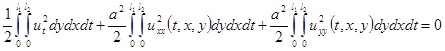 (3.17)
(3.17)
Интеграл, полученный из (3.17)
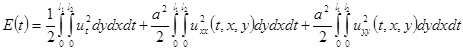 (3.18)
(3.18)
называется интегралом энергии балки. Мы видим, что 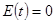 . Далее, из равенства нулю интеграла энергии следует, что
. Далее, из равенства нулю интеграла энергии следует, что 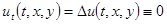 в области
в области 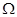 . Значит
. Значит 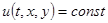 в области
в области 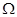 . А так как
. А так как 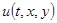 непрерывна в
непрерывна в 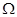 и
и 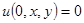 следует, что
следует, что 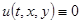 в
в 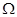 .
.
Полученные интегралы энергии представляют собой функционалы, зависящие от параметра времени 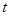 и физических характеристик, касающихся непосредственно рассматриваемого объекта, и сильно зависят от функции
и физических характеристик, касающихся непосредственно рассматриваемого объекта, и сильно зависят от функции 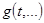 в правой части уравнений (1.1), (2.1) и (3.1) и начальных условий. Данные функционалы могут быть использованы в дальнейшем при решении задачи управления колебаниями мембраны, балки или пластины в зависимости от функции
в правой части уравнений (1.1), (2.1) и (3.1) и начальных условий. Данные функционалы могут быть использованы в дальнейшем при решении задачи управления колебаниями мембраны, балки или пластины в зависимости от функции 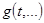 .
.
Литература:
1. Атамуратов А. Ж., Михайлов И. Е., Муравей Л. А. О гашении колебаний балки. Труды ИСА РАН. Динамика неоднородных систем. Т.50(1). –М.: Книжный дом «ЛИБРОКОМ», 2010. С. 53–58.
2. Атамуратов А. Ж., Михайлов И. Е. Численное решение задачи о гашении колебаний балки. Тезисы докладов Международной конференции по прикладной математике и информатике, посвященной 100-летию со дня рождения академика А. А. Дородницына. ВЦ РАН, Москва, 7–11 декабря 2010 г. С. 83–84.
3. Aslanov S., Atamuratov A., Mikhailov I., Muravey L., The damping of vibrations for mechanical systems // II International Conference «Optimization and applications» (OPTIMA-2011), Abstracts, Petovac, Montenegro, Sept. 25- Oct. 2, 2011. P. 34.
4. Muravey L., Mikhailov I., Atamuratov A., The damping problem of vibrations for large mechanical systems // ICIAM2011, Abstracts, Vancouver, Canada, July 18–22, 2011. P. 87.
5. Атамуратов А. Ж., Михайлов И. Е., Муравей Л. А. О гашении колебаний сложных механических структур // Авиакосмическая техника и технология, 2012, № 4. С. 54–59.
6. Atamuratov A., Mikhailov I., Muravey L. On the numerical damping of beam’s vibrations // VII International Aerospace Congress IAC’12. Abstracts. Moscow, Russia. 26–31 August, 2012. P. 31–32.
7. Атамуратов А. Ж. Исследование подходов к решению задач математической физики на примере уравнения колебаний прямоугольной мембраны // Молодой ученый. № 10. 2013. С. 1–5. http://www.moluch.ru/archive/57/6198/







