В работе предложена методология моделирования функционирования многоэлементных мобильных машин на плоской горизонтальной поверхности.
Ключевые слова: мобильная машина, математическая модель, динамика, модуль.
Вступление. Современные мобильные энергетические средства в машиностроении и сельском хозяйстве представляю собой многоэлементные мобильные машины с большим количеством степеней свободы. Примерами таких машин являются автомобили с прицепами и машинно-тракторные агрегаты. Стоит отметить, что широкозахватные посевные машинно-тракторные агрегаты состоят из трёх и более элементов, таких как трактор с шарнирно-сочленённой рамой, бункер для посевного материала и удобрений, сеялки прямого сева.
Анализ исследований и публикаций. Изучение вопросов динамики данных машин занимается большое количество учёных по разным направлениям. Основные направления исследований связаны с рассмотрением проблем движения данных машин устойчивости и управляемости.
В работе [1] рассматривается модель движения гусеничного трактора в составе пахотного агрегата на плоской горизонтальной поверхности и установлены зависимости увода от пройденного пути. В исследовании динамики грунто-обрабатывающего посевного агрегата [2] получены зависимости траекторий движения элементов агрегата от влияния оператора на рулевое управление. Горелов В. А. решал проблему моделирования движение многозвенных колёсных транспортных средств с учетом особенностей конструкций сцепных устройств [3]. Движение многоэлементных роботов (неголономных систем) с помощью уравнений Лагранжа второго рода связано с определёнными затруднениями, описанными в работе [4]. Проф. Рославцев предложил использовать методы, перечисленные в работе [5] для исследования динамики сельскохозяйственных тракторов и агрегатов. Устойчивость и управляемость для многоэлементного мобильного энергетического средства рассматривалась Надыкто В. Т. в монографии [6].
Постановка задания. Целью данной работы является, разработка методологии моделирования функционирования многоэлементных мобильных машин на плоской горизонтальной поверхности.
Изложение основного материала. Для исследования процессов совместного движения энергетического и технологического модулей рассмотрим обобщённую математическую модель движения первого из них. Поскольку предметом статьи является изучение взаимодействия энергетического и технологического модулей в процессе совместного движения, то в качестве базовой принята математическая модель движения гусеничной машины, как наиболее простой с точки зрения математического описания.
При моделировании движения мобильной машины (ММ) на местности используется единая для режимов прямолинейного движения и режимов поворота модель движения ММ на ровной горизонтальной поверхности с заданными характеристиками грунта. Неподвижная (земная) система координат (U, V) используется для определения траектории движения ММ (рис. 1).
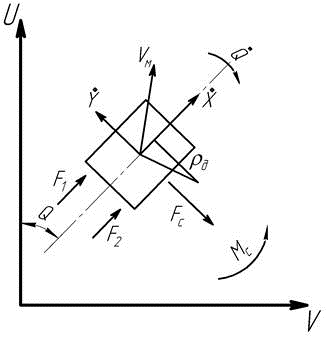
Рис. 1. Расчетная схема движения машины на местности: Vм — действительная скорость движения машины; F1, F2 — силы тяги на левом и правом борту; rд — действительный радиус поворота; Fс — сила сопротивления боковому смещению; Мс — момент сопротивления повороту
Для определения направления действия сил на корпус мобильной машины используется связанная система координат (Х, Y, Q). Производные координат (Х, Y, Q) имеют следующий физический смысл:  — текущая скорость в продольном направлении;
— текущая скорость в продольном направлении; 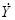 — текущая скорость в поперечном направлении (за положительное направление принимается движение влево);
— текущая скорость в поперечном направлении (за положительное направление принимается движение влево); 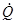 — угловая скорость поворота (за положительное направление принимается поворот по часовой стрелке). Текущее значение Q — курсового угла, отсчитывается от оси U по часовой стрелке.
— угловая скорость поворота (за положительное направление принимается поворот по часовой стрелке). Текущее значение Q — курсового угла, отсчитывается от оси U по часовой стрелке.
Координаты мобильной машины в неподвижной системе координат определяются в результате решения системы дифференциальных уравнений:
 (1)
(1)
Система дифференциальных уравнений движения машины на местности в принятых координатах имеет вид:
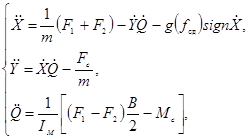 (2)
(2)
где g = 9,81 м/с2 — ускорение свободного падения;
m — масса машины;
fсд — суммарный от грунта и ходовой части коэффициент сопротивления движению;
F1, F2 — силы тяги на правом и левом борту, могут быть определены из решения модели кинематического и силового взаимодействия моторно-трансмиссионной установки с корпусом машины через систему «движитель-грунт»;
Fc — суммарная сила сопротивления боковому смещению;
Мc — суммарный момент сопротивления повороту.
Сила Fc и момент Мc зависят от поперечных сил:
 (3)
(3)
где mс — текущее значение коэффициента сопротивления повороту;
c — относительная величина смещения центра поворота в продольном направлении;
Fx — суммарная горизонтальная сила, действующая в продольном направлении:
Fх = F1 + F2 — M×g×fсд×sign. (4)
Относительная величина смещения центра поворота в продольном направлении:
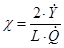 . (5)
. (5)
Если величина смещения центра поворота превосходит половину длины опорной поверхности, то c полагается равным ± 1, т. е.
—1 £ c £ 1. (6)
Коэффициент сопротивления повороту является эмпирической функцией радиуса поворота и определяется для больших (8) и малых (9) радиусов отдельно. В общем случае величина коэффициента сопротивления повороту определяется:
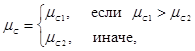 (7)
(7)
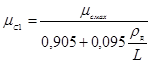 ; (8)
; (8)
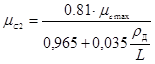 , (9)
, (9)
где mсмах — максимальное значение коэффициента сопротивления повороту (характеристика грунта);
rд — действительный радиус поворота:
 . (10)
. (10)
Математическая модель (1–10) рассматривалась, как обобщённая модель гусеничного трактора в составе пахотного агрегата [1].
Добавим в модель движения мобильной машины внешние узлы на расстоянии L1 и L2 от центра масс вдоль продольной оси, к которым в дальнейшем будет подсоединяться технологическое оборудование (рис. 2). Для каждого из узлов назначим локальную систему координат, совпадающую по направлению с локальной системой координат ММ. Таким образом, сформирована трехузловая модель движения ММ.
В соответствии с теоремой о мгновенном центре скоростей сформулируем выражения для определения скоростей движения узлов 1 и 2:
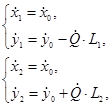 (11)
(11)
где 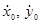 — скорость центра масс мобильной машины в глобальной системе координат.
— скорость центра масс мобильной машины в глобальной системе координат.
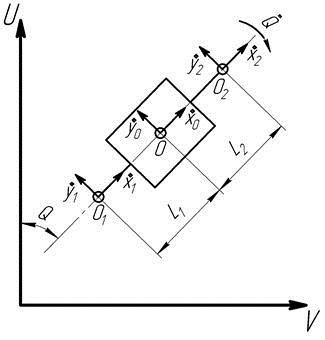
Рис. 2. Трехузловая модель движения мобильной машины.
Для формирования основных уравнений связи, исходя из (11), определим величины ускорений узлов 1 и 2 в глобальной системе координат:
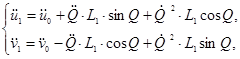 (12)
(12)
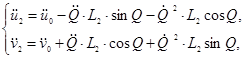 (13)
(13)
где 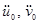 — ускорения центра масс ММ в глобальной системе координат:
— ускорения центра масс ММ в глобальной системе координат:
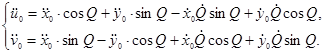 (14)
(14)
Рассмотрим силовой баланс системы состоящей из энергетического и технологического модулей для общего случая плоского движения (рис. 3).
В процессе взаимодействия машины с технологическим модулем в месте сцепления возникают реактивные силы равные по модулю и противоположные по направлению, передаваемому сцепкой, усилию. Таким образом, формируя уравнения движения можно отбросить одну из машин, заменив ее влияние реактивной силой.
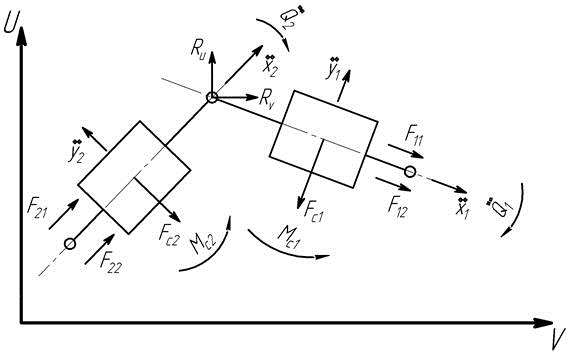
Рис. 3. Динамическая модель движения энергетического и технологического модулей: Fi,j — тяговые усилия на мобильной тяговой машине и технологическом модуле, i — номер машины, j — индекс борта; Мсі — момент сопротивления повороту; Fсi — сила сопротивления боковому смещению; Ru — проекция вектора реактивной силы, действующей в сцепном устройстве, на ось U; Rv — проекция вектора реактивной силы, действующей в сцепном устройстве, на ось V
Уравнение движения первого элемента (энергетического модуля) можно определить:
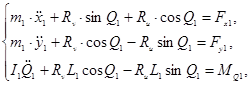 (15)
(15)
где m1 — масса первой машины;
Fх1 — обобщенная сила, действующая на первую машину в продольном направлении, которая определяется из формулы (4):
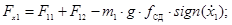 (16)
(16)
Fу1 — обобщенная сила, действующая на первую машину в поперечном направлении, которая равна силе сопротивления боковому смещению (3) и противоположна ей по направлению:
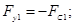 (17)
(17)
MQ1 — обобщенный момент первой машины, который определяется в соответствии с формулой (3):
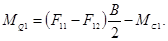 (18)
(18)
Система уравнений движения второго элемента (технологического модуля):
 , (19)
, (19)
где m2 — масса второй машины;
Fх2 — обобщенная сила, действующая на вторую машину в продольном направлении, которая определяется из соотношения (4):
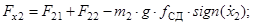 (20)
(20)
Fу2 — обобщенная сила, действующая на вторую машину в поперечном направлении, которая равна силе сопротивления боковому смещению (3) и противоположна ей по направлению:
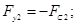 (21)
(21)
MQ2 — обобщенный момент второй машины, который определяется в соответствии с (3):
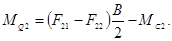 (22)
(22)
В качестве уравнений связи используем очевидное равенство проекций линейных ускорений на оси U и V:
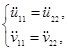 (23)
(23)
где 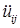 — ускорение i-го узла j-й машины в направлении оси U;
— ускорение i-го узла j-й машины в направлении оси U;
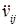 — ускорение i-го узла j-й машины в направлении оси V.
— ускорение i-го узла j-й машины в направлении оси V.
Решая совместно уравнения (15, 19) и уравнения связи (23) получаем следующую систему дифференциальных уравнений движения многоэлементного агрегата:
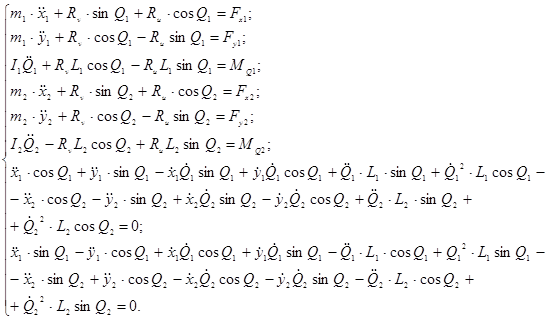 (24)
(24)
В результате решения системы (24) получаем вектор D:
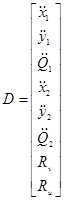 (25)
(25)
Проинтегрировав величины ускорений энергетического и технологического модулей и подставив в выражение (1) значения линейных скоростей и курсового угла получим скорости движения первой и второй машин в глобальной системе координат. Последующие интегрирование позволит получить величины перемещений для обеих машин и определить их координаты на местности.
Выводы. Предложенная методология моделирования функционирования многоэлементных мобильных машин на плоской горизонтальной поверхности может быть использована для машин с любым типом движителя и для любого количества одновременно сцепленных машин. Она позволяет автоматизировать процесс составления математических моделей совместного движения мобильных машин, что в свою очередь позволяет снизить затраты времени на составление уравнений движения элементов системы.
Литература:
1. Лебедев, А. Т. Увод гусеничного трактора с гидрообъемным механизмом поворота на пахотных работах [Текст] / А. Т. Лебедев, С. А. Лебедев, В. А. Толстолуцкий // Механизация сельского хозяйства: Весник ХНТУСХ. — Х.: ХНТУСХ. — 2005. — Вып. 41. — С. 37–42.
2. Лебедєв, А. Т. Математична модель руху комбінованого посівного агрегату в складі трактора ХТЗ-150К-09 та сівалки прямої сівби АПП-6 при впливі оператора на рульове керування [Текст] / А. Т. Лебедєв, Р. В. Антощенков // Системи обробки інформації — Х.: ХУПС, 2009. — Вип. 3 (77). — С. 135–138.
3. Горелов, В. А. Математическое моделирование движения многозвенных колесных транспортных комплексов с учетом особенностей конструкций сцепных устройств [Текст] / В. А. Горелов // Электрон. жур. «Наука и образование: электронное научно-техническое издание». — 2012. — № 2. http://technomag.edu.ru/doc/343394.html.
4. A. De Luca. Modelling and control of nonholonomic mechanical systems [Text] / A. De Luca, G. Oriolo // Kinematics and Dynamics of Multi-Body Systems (J. Angeles, A. Kecskemethy Eds.). Springer-Verlag. — 1995. — pp. 301–305.
5. Рославцев, А. В. Методы исследования движения МТА [Текст] /А. В. Рославцев, В. А. Хаустов, В. М. Авдеев, В. М. Третяк, И. П. Сазонов, Е. Э. Гурковский // Тракторы и селькохозяйственные машины. — 1998. — № 6. — С. 24–28.
6. Надыкто В. Т. Основы агрегатирования модульных энергетических средств [Текст] / В. Т. Надыкто. — Мелитополь: КП «ММД», 2003. — 240 с.







