В статье рассмотрены методические аспекты формированияпрофессиональной компетентности будущего учителя начальной школы при обучении стохастике. Выявлены основные направления и особенности методики формирования первоначальных стохастических представлений младших школьников.
Ключевые слова: профессиональная компетентность, стохастика, первоначальные стохастические представления.
Одним из аспектов модернизации содержания математического образования является включение в школьные программы элементов комбинаторики и теории вероятностей, что обусловлено ролью вероятностно-статистических знаний в общеобразовательной подготовке современного человека. Внедрение элементов стохастики в курс математики средней школы в виде одной из сквозных содержательно-методических линий влечет за собой необходимость пропедевтической работы в начальной школе. Смена приоритетов целей начального образования, переход на четырехлетнее обучение, вариативность его учебно-методического обеспечения требуют и соответствующих изменений математической подготовки будущих педагогов. Становится необходима профессиональная подготовка учителей начальных классов к формированию у младших школьников первоначальных стохастических представлений.
Различные стороны обучения вероятностно-статистическому содержанию изучены Л. О. Бычковой, А. Я. Дограшвили, В. Д. Селютина, А. Плоцки и др. Концепция профессионально-педагогической направленности специальной подготовки студентов педвузов разработана и реализована в исследованиях В. Д. Селютина. Работы И. Б. Лариной, Э. А. Мирошниченко, С. А. Самсоновой направлены на решение проблем профессиональной подготовки будущих учителей математики при обучении стохастике. Исследования Л. С. Выготского, О. С. Медведевой, В. В. Давыдова, Б. Г. Гейдмана, А. Г. Рубиной, А. П. Тонких и др. показывают, что развитие у учащихся способностей к комбинациям и перестановкам предметов намного эффективнее начинать в начальной школе.
Можно констатировать, что вопросы формирования профессиональной компетентности будущего учителя нашли свое отражение в научно-методических исследованиях, однако нет специального исследования с позиций компетентностного подхода к формированию профессиональной компетентности будущего учителя начальной школы в области создания первоначальных стохастических представлений младших школьников. Вместе с тем, можно утверждать, что сейчас в теории педагогики и методики преподавания сложились необходимые предпосылки, позволяющие подойти к решению данной проблемы.
Изучение и анализ работы учителей по внедрению стохастической содержательно-методической линии в процесс обучения начальной школы позволяют сделать вывод, что основные причины трудностей кроются в недостатках их профессионально-педагогической подготовки [1, с. 95].
Таким образом, актуализация проблемы формирования профессиональной компетентности будущего учителя начальной школы обусловлена наличием противоречий в системе современного образования между:
- содержанием современного педагогического образования в области комбинаторики и теории вероятности и требованиями, предъявляемыми в настоящее время школой, обществом, государством к уровню профессиональной подготовки учителя начальной школы в данной области;
- потребностью обеспечения учителей начальных классов методикой формирования первоначальных стохастических представлений младших школьников и недостаточной разработанностью этой проблемы.
Разрешение названных противоречий мы рассматриваем в контексте решения проблемы исследования: выявление теоретических, методических и организационных условий формирования профессиональной компетентности будущего учителя начальной − системы взаимосвязанных компонентов: фундаментальных предметных знаний, методических умений; профессионально-педагогических знаний и умений, профессионально значимых качеств личности учителя, которые реализуются в педагогической деятельности [2].
Эффективность подготовки учителей начальных классов в области формирования у младших школьников первоначальных стохастических представлений, будет достигнута, если подготовка построена на общих теоретических основаниях как система непрерывного педагогического образования, одной из целей которой является формирование профессиональной компетентности учителя начальных классов в указанной области [3, с.9].
Основы проектирования модели формирования профессиональной компетентности будущих специалистов при обучении стохастике исследованы в нами в работах «Теоретические и методические основы изучения комбинаторики в начальной школе», «Теоретические и методические основы изучения элементов теории вероятностей в начальной школе», «Концептуальная модель формирования профессиональной компетентности будущих учителей начальной школы при обучении стохастике» и др. [3–6].
Основы профессиональной компетентности учителя формируются в вузе путем установления органической связи между теорией и практикой, что должно быть реализовано путем интеграции предметных знаний и освоения методики преподавания элементов стохастики в системе начальной школы. При формировании профессиональной компетентности педагога одинаково важны уровень его фундаментальной подготовки по базовой дисциплине и методической подготовки. Возникает проблема формирования методической компетентности студентов, способных к успешной реализации вероятностно-статистической содержательно-методической линии в начальном курсе математики.
Для овладения специальной методикой обучения стохастике необходимо наличие следующих компонентов: знание концептуальных основ стохастической содержательно-методической линии; знание содержания данного раздела математики в методическом проецировании на школьное обучение; знание методических приемов руководства познавательной деятельностью учащихся и умение применять их на практике [7, C. 247].
Разработанная нами концептуальная модель формирования профессиональной компетентности студентов - будущих учителей начальной школы отражает характерные свойства, связи и отношения методической системы в доступной для анализа форме и обеспечивает переход теоретической сущности исследуемой проблемы в практическую действительность [1, 2]. Практика работы показывает, что необходимо:
- обучение студентов содержательной основе стохастики, истории ее возникновения и развития, основополагающим идеям и принципам данного раздела математики;
- знание студентами целей изучения элементов комбинаторики, теории вероятностей и математической статистики, развивающего потенциала и способа его реализации, результатов обучения, которыми должен овладеть выпускник начальной школы;
- формирование умений осуществлять компетентный анализ содержания программ, учебников математики, осуществлять перспективное планирование, проводить анализ логической структуры темы, отбор материала для формирования первоначальных вероятностных представлений младших школьников.
Данные требования определяют уровень вероятностно-статистической и методической подготовки студентов факультета педагогики и методики начального образования.
В содержании стохастической содержательно-методической линии выделяют три взаимосвязанных направления, методикой работы над которыми должен владеть будущий учитель:
- подготовка младших школьников в области комбинаторики, с целью создания в дальнейшем аппарата для решения вероятностных задач;
- формирование первоначальных представлений о случайных событиях, о вероятностях событий;
- подготовка в области математической статистики: формирование умений, связанных с представлением, сбором данных и их интерпретацией.
В понятии компетентности заложена идеология интерпретации содержания образования, формируемого как ожидаемый результат обучения. Методическая компетентность учителя ориентирована на достижение младшим школьником итоговых результатов обучения, отраженных в требованиях к уровню знаний, умений и навыков выпускника начальной школы. В результате изучения стохастики учащиеся начальной школы должны:
- понимать смысл требования «перечисли все возможные варианты», осуществлять систематический перебор всех возможных вариантов при решении комбинаторных задач;
- понимать и правильно употреблять термины: «невозможно», «возможно», «случайно», «чаще», «реже»;
- понимать и извлекать информацию из простой таблицы, уметь записать данные, содержащиеся в тексте, в таблицу;
- уметь фиксировать исход простейшего случайного эксперимента, осуществлять регистрацию результатов наблюдений.
Приступая к обучению стохастике, учитель нацеливает свою деятельность на достижение такого уровня.
Со случайными событиями можно встретиться всюду, где имеют место непостоянные причинные связи, где действуют многочисленные факторы, не поддающиеся учету. В практической жизни, в различных видах деятельности младшие школьники могут познакомиться с проявлениями процессов стохастической природы. Окружающая действительность, становясь объектом познания, способствует накоплению представлений о случайностях, разумеется, в самой конкретной, наглядной и простейшей форме. Таким образом, уже младшие школьники могут быть ознакомлены с такими сторонами действительности, ситуациями и фактами, которые позволяют акцентировать их внимание на особенностях явлений, имеющих ярко выраженную стохастическую природу [7, с. 63].
В психологии под представлениями понимают наглядные образы предметов или явлений, возникающие на основе прошлого опыта (данных ощущений и восприятий) путем воспроизведения их в памяти или в воображении. Под стохастическими представлениями понимают представления о мире случайных явлений, с нежесткими связями между ними.
Сталкиваясь с конкретными проявлениями случайностей, человек постепенно получает представления о них. Познание ребенком окружающего мира происходит от восприятия единичных предметов и явлений к образованию конкретных представлений и от обобщения последних к формированию понятий. Поэтому началом формирования стохастических представлений можно считать восприятие детьми единичных случайных явлений, при этом оптимальным методом выделения характерных свойств случайного явления служит непосредственное наблюдение самого этого явления. В процессе проведения наблюдения важно показать младшим школьникам, что многие явления отличаются непостоянством. Одни события обязательно наступают, другие никогда не наступают, третьи − могут наступить, а могут и не наступить при данном комплексе условий. Одни результаты наблюдений получаются чаще, а другие реже, при этом в некоторых случаях результаты почти не отличаются друг от друга, а в других очень сильно рознятся. Таким образом, в процессе наблюдений явлений стохастического характера, у учащихся формируются самые первые вероятностно-статистические представления.
Одним из принципов формирования содержания общего образования является принцип единства содержательной и процессуальной сторон обучения [8, с. 3–6]. Реализация принципа требует отбора стохастического содержания с учетом закономерностей формирования статистического мышления в соответствии с концепцией построения стохастической содержательно-методической линии.
В педагогической психологии усвоение нового тесно связано с осуществлением предметных действий. В процесс формирования первоначальных статистических представлений необходимо включить предметные действия учащихся с объектами, которые обеспечивают основу познания случайных явлений. В структуре психики учащихся младшего школьного возраста, важную роль играет конкретно-образное мышление. Работая с предметами, младшему школьнику легче наблюдать за своими действиями и управлять ими. Исходя из этого, возникает задача определения видов предметной деятельности, соответствующих возрасту учащихся начальной школы, в которых были бы использованы максимальные возможности для формирования стохастических представлений.
Наглядное отражение особенностей случайных явлений и возможность их массового наблюдения может быть осуществлено в процессе игры. Под игрой понимают вид непродуктивной деятельности, мотив которой заключается в самом процессе. В игровой деятельности учащихся отражается опыт и культура, потребности и мотивы каждого. Несмотря на то, что в школьном возрасте учение становится ведущим видом деятельности, младших школьникам присущи игровые интересы, поэтому нельзя не учитывать обучающего и развивающего влияния игры. Игровая и учебная деятельность перерастают одна в другую, оказывая развивающее воздействие на учащихся, приучая видеть неоднородность и многообразие явлений, выделять из них случайные и закономерные. Игра, включенная в целостный педагогический процесс, становится средством воспитания.
Стохастическими называют игры, в которых возможно наблюдение явного, отчетливого проявления фактов стохастической природы [7, с. 92].
Приведем примеры игр и заданий, которые можно использовать при знакомстве младших школьников с понятиями теории вероятностей.
Пример. Положим в мешок 3 красных, 3 белых и 3 зеленых шара. Какое событие более вероятно: извлечь шары 3 цветов или двух≤
Производятся последовательные извлечения с возвращением групп по четыре шара, то есть вытаскиваются четыре шара, записываются их цвета, после чего шары возвращаются в мешок и ее содержимое перемешивается.
Целесообразна следующая система вопросов. Можно ли получить все шары одного цвета≤ Можно ли получить шары четырех цветов≤ Какой из этих случаев более вероятен≤ Учащиеся производят десять последовательных извлечений. Как вы думаете, будут более часто получаться два цвета или три≤ Или одинаково часто≤
В каком из случаев имеется наибольшая возможность получить шары трех цветов - если вытащить 3, или 4, или 5, или 6 шаров≤
При проведении игры целесообразно использовать технологию работы в группах по два-три человека. Так они могут произвести большое количество испытаний; тогда учащиеся убедятся, что более вероятно вытащить 3 цвета, нежели два. От них можно даже ожидать неких зачаточных рассуждений, объясняющих этот результат.
Данная ситуация направлена на развитие представлений младших школьников о невозможных событиях, достоверных событиях, а в отношении случайных событий, на формирование понятий более вероятное событие, менее вероятное событие.
Пример. Игра «Сколько окажется на своём месте≤» Эта игра помогает на интуитивном уровне подвести учащихся к понятию относительной частоты.
Учащимся предлагают 5 одинаковых карточек с изображенными на них цифрами от 1 до 5, затем перетасовывают их и выкладывают на стол в той последовательности, в которой они оказались после перетасовывания, например, в такой: 3, 1, 4, 2, 5. При этом только одна цифра - «5» — соответствует номеру места, на котором она лежит.
Далее можно сформулировать серию вопросов, на которые учащиеся должны ответить на основании данных, полученных в ходе экспериментов.
Как вы думаете, насколько редким является данный исход≤ Будет ли ещё более редким случай, когда ни одна карточка не окажется на своем месте≤ Будет ли случай, когда все карточки лежат на своем месте≤ Что можно сказать о частоте исхода, когда две (три, четыре) цифры окажутся на своем месте≤
Многие популярные среди детей игры предполагают использование игрального кубика, исходы подбрасываний которого определяют число шагов в продвижении игрока к цели. При подбрасывании кубика дети имеют возможность наблюдать отчетливо выраженные случайные события.
Пример. Игра «Какова сумма≤» поможет подвести учащихся к понятию вероятности с точки зрения классического определения.
Нарисуем прямоугольник 14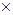 11 клеток. Между 14 детьми распределим 14 жетонов, пронумерованных от 1 до 14. Учащиеся ставят свои домики на линию старта на клетку с соответствующим номером. Бросаем две большие игральные кости. После каждого подбрасывания костей ребенок, номер которого равен сумме очков на выпавших гранях, продвигается на одну клетку к финишу. Выигрывает тот, кто первым достигнет финиша.
11 клеток. Между 14 детьми распределим 14 жетонов, пронумерованных от 1 до 14. Учащиеся ставят свои домики на линию старта на клетку с соответствующим номером. Бросаем две большие игральные кости. После каждого подбрасывания костей ребенок, номер которого равен сумме очков на выпавших гранях, продвигается на одну клетку к финишу. Выигрывает тот, кто первым достигнет финиша.
Очень скоро учащиеся догадываются, что некоторые из них находятся в более благоприятных условиях, чем другие, и что участники, получившие номера 1, 13, 14, не имеют никакого шанса продвинуться вперед: имея 2 кости, невозможно в сумме получить 1 или число, большее 12. Тогда учащиеся решают, что в следующей партии эти числа надо отбросить. Следует обосновать, почему так происходит, изучив, сколькими способами можно получить 2, 3, 4,…,12 очков при бросании двух игральных костей.
На определенном этапе в игре младшие школьники начинают проявлять некоторые черты исследовательской деятельности, что влечет за собой переход от игр к экспериментам. Под статистическим экспериментом понимают предметную деятельность, направленную на изучение искусственно вызываемых случайных явлений при соблюдении определенного комплекса условий. В отличие от стохастической игры, предполагающей простое наблюдение случайного явления, статистический эксперимент содержит в себе учет наблюдаемых фактов.
Если школьник, неоднократно подбрасывая игральный кубик, ведет учет результатов испытаний, чтобы по ним сделать какие-то выводы, то в этом случае он проводит статистический эксперимент. Разделение на игры и эксперименты довольно условно: мы приводили примеры игр, в которых содержатся элементы экспериментирования, с другой стороны, статистические эксперименты во многих случаях могут быть организованы в форме игр.
Пример. Покажем группе учащихся 19 шаров, 8 из которых желтые, 6 — синие, а 5 — красные. Положим шары в мешок, перемешаем и вытащим сразу два. Однако перед тем, как их вытаскивать, попросим младших школьников угадать цвета обоих шаров.
Чтобы учащимся не пришлось запоминать число шаров каждого цвета, положим на стол 8 желтых, 6 синих и 5 красных жетонов. На первом этапе целесообразно извлекать шары без возвращения: тогда ситуация будет меняться после каждого извлечения, что в большой степени стимулирует активность учащихся. Затем перейдем к извлечению пар шаров с возвращением: теперь младший школьник может сравнить свой ответ с результатом извлечения и постепенно улучшить стратегию, так как ситуация восстанавливается после каждого извлечения, и, следовательно, вероятности всех событий остаются постоянными, а все изменения вызваны случаем. Учащихся полагают, что, безусловно, с большей вероятностью можно вытащить два желтых шара, чем желтый и синий шары, поскольку желтых шаров больше, чем синих и чем красных. На деле все обстоит наоборот.
Эксперимент сам по себе здесь недостаточен. Наилучшим способом вызвать на размышление является расхождение между предположениями и опытом. Для этого можно представить аналогичную, но более простую ситуацию: положим в мешок 2 белых шара и 1 черный.
В игре младшие школьники отражают окружающую действительность, познают те или иные доступные их восприятию и пониманию факты, явления. Используя игру как средство ознакомления с окружающим миром, педагог может направить внимание учащихся на явления, которые ценны для расширения круга представлений. Руководя игрой, педагог воспитывает стремление узнавать, искать, проявлять усилие, находить, что содействует умственному и общему развитию личности ребенка.
Внедрение данного подхода к осуществлению образовательного процесса позволяют студентам овладеть методикой формирования первоначальных стохастических представлений младших школьников в такой степени, чтобы они могли не только осознанно применять полученные знания в процессе обучения и работы, но и, по мере необходимости, углублять и расширять их путем дальнейшего самообразования.
Литература:
1. Проценко Е. А., Трофименко Ю. В. Формирование профессиональной компетентности будущих учителей начальной школы при обучении стохастике. Вестник Таганрогского государственного педагогического института. 2013. № 1. С. 094–100.
2. Проценко, Е. А. Концептуальная модель формирования профессиональной компетентности будущих учителей начальной школы при обучении стохастике//Вопросы гуманитарных наук. -2008. -№ 3 (36). -С. 285–292.
3. Проценко, Е. А. Теоретические и методические основы изучения элементов теории вероятностей в начальной школе/Е. А. Проценко, Г. А. Семенова. -Таганрог: Изд-во Таганрог. гос. пед. ин-та, 2009. -228 с. 5.
4. Проценко, Е. А. Теоретические и методические основы изучения комбинаторики в начальной школе/Е. А. Проценко, Г. А. Семенова. -Таганрог: Изд-во Таганрог. гос. пед. ин-та, 2008. -128 с.
5. Проценко, Е. А. Использование информационных технологий как средства организации самостоятельной работы студентов//Известия высших учебных заведений. Северо-Кавказский регион. Серия: Естественные науки. -2006. -№ S16. -С. 77–81.
6. Проценко, Е. А. Применение компьютерных средств обучения в процессе преподавания комбинаторики//Вестник Московского городского педагогического университета. -2006. -№ 6. -С. 167–170.
7. Селютин В. Д. Научные основы методической готовности учителя математики к обучению школьников стохастике: Дис.... д-ра пед. наук. М., 2002. с.247.
8. Краевский В. В. Содержание образования: вперед к прошлому. -М.: Педагогическое общество России, 2001.







