В настоящий момент основные трудности вычисления когомологии простых модулей односвязных алгебраических групп с неприводимой системой корней над полем положительной характеристики связаны структурными вопросами модулей Вейля. Одним из эффективных методов изучения модуля Вейля является построение фильтрацию Янцена. Общие свойства фильтрации Янцена для модулей Вейля изучены в работах [1] – [10]. Характеры простых модулей полностью вычислены только для малых алгебраических групп с системами корней типов 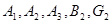 . Из результатов исследовании, полученные к настоящему моменту видно, что структура модулей Вейля не получены даже для ограниченных старших весов. В данной заметке построены фильтрации Янцена для некоторого семейства модулей Вейля для алгебраической группы
. Из результатов исследовании, полученные к настоящему моменту видно, что структура модулей Вейля не получены даже для ограниченных старших весов. В данной заметке построены фильтрации Янцена для некоторого семейства модулей Вейля для алгебраической группы 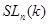 над полем
над полем 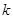 характеристики
характеристики 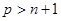 .
.
Пусть 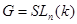 и
и 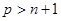 . Обозначим через
. Обозначим через 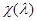 формальный характер модуля Вейля
формальный характер модуля Вейля 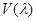 и через
и через 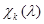 формальный характер простого
формальный характер простого 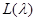 со старшим весом
со старшим весом 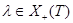 , где
, где 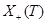 – множество доминантных весов. Будем предполагать, что система корней
– множество доминантных весов. Будем предполагать, что система корней 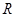 группы
группы 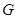 неприводима и обозначим максимальную корень системы
неприводима и обозначим максимальную корень системы 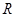 через
через 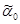 . Действие аффинной группы Вейля
. Действие аффинной группы Вейля 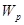 определяется формулой
определяется формулой
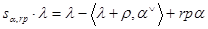 ,
,
где 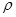 – полусумма положительных корней.
– полусумма положительных корней.
Рассмотрим следующие элементы множества ограниченных весов 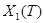 :
:
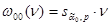 ,
, 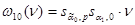 ,
, 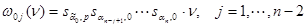 ,
,
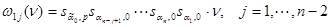 ,
,
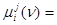
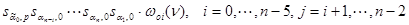 ,
,
где 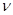 – элемент внутри нижнего фундаментального аффинного алькова.
– элемент внутри нижнего фундаментального аффинного алькова.
Предложение. Пусть 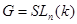 и
и 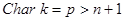 . Тогда
. Тогда 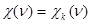 и
и
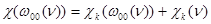 ,
,
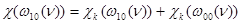 ,
,
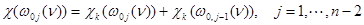 ,
,
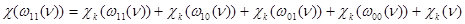 ,
,
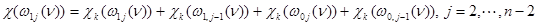 ,
,
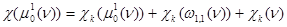 ,
,
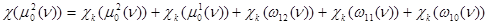 ,
,
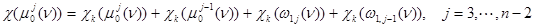 ,
,
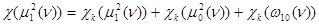 ,
,
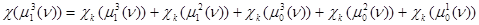 ,
,
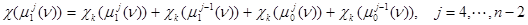 ,
,
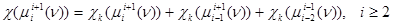 ,
,
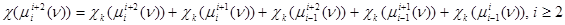 ,
,
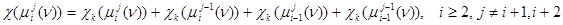 .
.
Доказательство. Следует из формулы суммирования фильтрации Янцена ( [2], стр.133) для модуля Вейля и принципа перехода ([3], стр.297).
Следствие. Для короткой точной последовательности 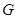 -модулей
-модулей 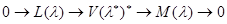 имеют место следующие изоморфизмы
имеют место следующие изоморфизмы 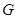 -модулей:
-модулей:
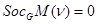 ,
,
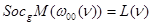 ,
,
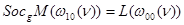 ,
,
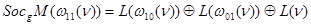 ,
,
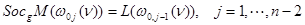 ,
,
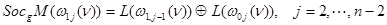 ,
,
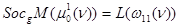 ,
,
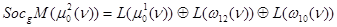 ,
,
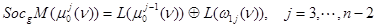 ,
,
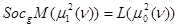 ,
,
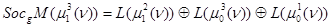 ,
,
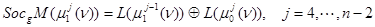 ,
,
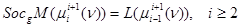 ,
,
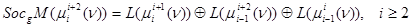 ,
,
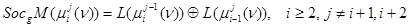 .
.
Заметим, что глубина фильтрации Янцена всех рассматриваемых модулей Вейля не больше чем 2. Тогда доказанное предложение и его следствие полностью определяют фильтрацию Янцена рассматриваемого семейства модулей Вейля.
Замечание. Формулы формальных характеров 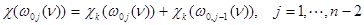 , были описаны ранее Янценом и остается верным и для других простых односвязных алгебраических групп.
, были описаны ранее Янценом и остается верным и для других простых односвязных алгебраических групп.
Литература:
1. Jantzen J.C. Darstellungen halbeinfascher gruppen und contravariante formen // J. reine angew. Math. - 1977. - vol. 290. - P. 117-141.
2. Jantzen J.C. Zur characterformel gewisser darstellungen halbeinfascher gruppen und Lie-algebren // Math. Z. - 1974. - Vol. 140. - P. 127-149.
3. Jantzen J.C. Weyl modules for groups of Lie type in M. Collins ed., Finite simple groups. London, New York: Acad. Press, 1980. P. 291-300.
4. Andersen H.H. Modular representations of finite groups of Lie type in M. Collins ed., Finite simple groups. London, New York: Acad. Press, 1980. P. 259-290.
5. Wong W.J. Irreducible modular representations of finite Chevalley groups // J. Algebra. - 1972. - Vol. 20. - P. 355-367.
6. Carter R.W., Lustig G. On the modular representations of the general linear an symmetric groups // Math. Z. - 1974. - Vol. 136. - P. 193-242.
7. Jantzen J.C. Uber das dekompositionsverhalten gewisser modularer darstellungen halbeinfascher gruppen und ihrerLie-algebren // J. of Algebra. - 1977. - vol. 49. - P. 441-469.
8. Vogan D. Irreducible characters of semisimple Lie groups I // Duke Math. J. - 1979. - Vol. 46. - P. 61-108.
9. Carter R. W., Payne M.T.J. On homomorphisms between Weyl modules and Specht modules // Math. Proc. Cambridge Philos. Soc. - 1980. - Vol. 87. - P. 419-425.
10. Andersen H.H. On the structure of Weyl modules // Math Z. - 1980. - V. 170. - P. 1-14.







