Задачами обучения студентов математике в системе высшего образования являются: научить студентов самостоятельно выделять главное в изучаемом материале, составлять и уметь применять алгоритмы решения задач, обучить студентов находить рациональные приемы решения теоретических и практических задач, критически осмысливать полученные результаты, уметь использовать их в дальнейшем.
Учебный материал по математическим дисциплинам условно разделяют на два блока: 1) теоретические знания; 2) математические задачи. Теоретический блок, с точки зрения форм и методов познания, представлен так: понятия и их определения; утверждения (теоремы, свойства, правила, формулы, признаки и т.п.); алгоритмы; математические методы (аксиоматический, координатный, векторный, векторно-координатный, метод уравнении и неравенств, метод подобия, моделирование и др.); математические идеи, факты и др.
Математика – наука дедуктивная, т.е. основана на умозаключениях от общего к частному. Важно формировать у студентов навыки дедуктивного мышления: умение выводить логические следствия из данных предпосылок, воспитывать умение анализировать данный вопрос, вычленять из него частные случаи [1].
Методика обучения математическим дисциплинам в вузе предполагает разработку и реализацию системного подхода к изучению основных компонентов, ведущий к глубокому и осознанному усвоению студентов логической основы курса математики. При этом каждый студент должен твердо знать логическое строение самой математики, создающий целостную картину усвоенных знаний, позволяющий выделить среди них опорные знания. Очевидно, что студенты не уясняют логику изучаемого предмета в целом, системы внутренних связей между его элементами. К сожалению, вопрос о логическом строении математики, когда и в каком объеме его изучать все еще остается нерешенной проблемой. Как показывает практика, выпускники школ имеют скудные сведения о логической конструкции геометрии в частности, и математики вообще. В результате вся математика воспринимается студентами в виде не связанных друг с другом фактов, предложении и формул. Тем не менее, как показало наше исследование, при определенной работе можно добиться некоторых успехов, если внимание студентов обращать на дедуктивность изложения математики на аксиоматической основе. Мы считаем, что необходимо на определенном этапе изучения математики наглядно показать составные части логического строения математики. Например, на рисунке 1 показано логическое строение школьного курса математики (геометрии и алгебры).
Рис 1. Модель логического строения математики
Составные части логического строения математики
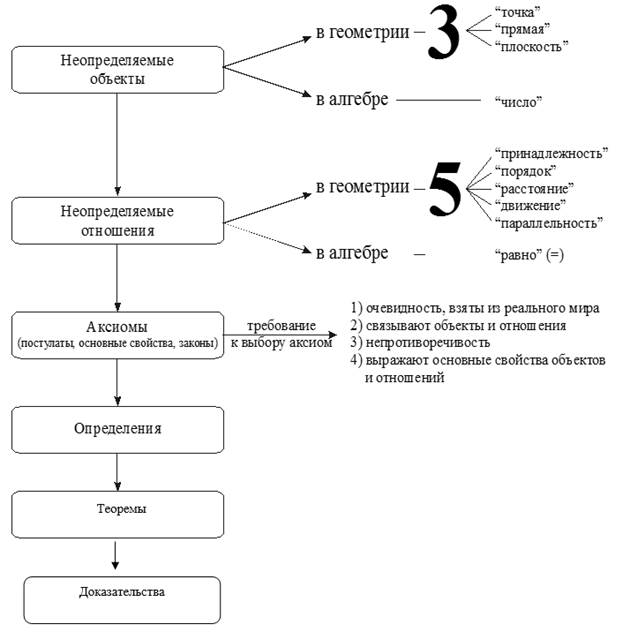
Под логическим строением математики понимают выделение объектов, указание отношений между объектами, принятие аксиом, формулировка определений отдельных понятий, теорем, установление истинности данного суждения путем доказательства. Данное определение применимо ко всем разделам математической теории.
Логическим фундаментом обоснования таких математических дисциплин как геометрия, арифметика, алгебра и другие являются система аксиом. При этом система аксиом должна быть непротиворечивой, т.е. из неё нельзя вывести путём логических рассуждений два взаимно противоположных утверждения; должна быть полной, т.е. нельзя её дополнить новыми аксиомами, не противоречащими уже принятым и не вытекающими из неё; должна быть независимой, т.е. если никакая из аксиом этой системы не является следствием других аксиом этой же системы [2].
Следует учесть, что в зависимости от выбора первичных понятий, меняется и система аксиом. Понятия, которые являются первичными, неопределяемыми при одном способе построения курса математики, могут оказаться определяемыми при других способах построения этого курса.
Основной целью современного метода обучения студентов является развитие познавательности активности и умственных способностей студентов, а это самым наилучшим образом возможно при самостоятельном отыскании доказательств теорем и решении задач на доказательство. К сожалению, для большей части студентов этот навык вызывает большие трудности. Основной причиной является незнание студентов общих методов доказательств теорем, их сущности, условии применимости при решении задач. Зная логическую сущность каждого из общих методов доказательства, студент сумеет построить свои рассуждения, установить правила пользования им.
Модель изучения логического строения математики объединяет в единое целое выделенные нами основные компоненты, включает в себя все этапы формирования математических понятий и определений, работу с теоремами и доказательствами, типы и виды упражнении, направленные на достижение определенной цели.
Например, методика формирования математического понятия включает в себя следующие действия: распознание объектов, относящиеся к данному классу. Для этого применяют логическое правило «подведение под понятие». Предварительно студенты должны быть ознакомлены с особенностями свойств: существенные – несущественные, необходимые – достаточные, необходимые и достаточные одновременно.
Таблица 1
Ошибки студентов при работе с математическими понятиями и меры по их предупреждению
|
Ошибки, встречающиеся в ответах студентов при работе с понятиями |
Меры по их предупреждению |
|
1. Неверное указание на родовое понятие по отношению к определяемому понятию. 2. Пропуск существенных признаков в определении. 3. Смещение понятий «определение», «теорема», затруднение использовать определение при выполнении упражнений. 4. Указание излишних признаков или «порочный круг». |
1. Ознакомление студентов с правилами построения формулировки определения понятий; в заключение темы полезно строить схему классификации изученных понятий; включать в задание воспроизведение последовательного обобщения (или ограничения) понятия и. т. д. 2.Анализ формулировки определения сразу после её введения на занятии; постановка вопросов вида «почему?»; выполнение заданий типа «найти ошибку в определении»; упражнении по неверно сформулированному студентом определению и.т. д. 3. Разъяснение смысла понятия «определение»; «аксиома»; «теорема» и. т. д., уделить внимание приемам введения понятия. 4.Акцентирование внимания на строгость понятия для включения в формулировку свойства понятия или в формулировки аксиом и теорем. |
В целом, в процессе введения и изучения математических понятий полезно:
- не вводить новых понятий формально; детально конкретизировать новые абстрактные понятия; по возможности применять конкретно-индуктивный метод;
- вводить понятия наиболее естественным для студентов путем; чаще привлекать студентов к самостоятельному изучению и определению рассматриваемого понятия, мотивировать вводимые понятия, термины, определения;
- выявить связи нового понятия с уже известными, указывать на аналогию в характеристике новых понятий и известных понятий;
- на каждом занятии полезно повторять определения, требуя правильной передачи сущности определения данного понятия, следить за речью студентов, требовать четкости, краткости, строгости в определении.
Исследования показали, что при таком подходе формирование понятий, их усвоение будет устойчивым, осознанным, системным (т.е. при этом понятия усваиваются не изолированно друг от друга, а как элементы единой системы), а следовательно, условием эффективного развития логического мышления студентов.
Необходимым условием развития логического мышления студентов является знание и применение мыслительных операций при формировании математических понятий, работе с аксиомами, теоремами, доказательствами, алгоритмами, формирование понятии о логическом строении разделов математики.
Повышение эффективности существующего обучения математике необходимо осуществлять за счет полного и последовательного формирования у студентов полноценных знаний основ наук, обеспечивающей единство управления процессом усвоения знании и системы умственных действий. При этом у студентов развивается логическое мышление, они видят диалектическую связь между математическими знаниями и реальной действительностью, овладевают приемами мыслительной деятельности, понимают сущность индуктивных рассуждений и дедуктивных доказательств, знают и умеют применять различные методы доказательств при решении конкретных задач.
Анализ современных концепций формирования активной познавательной учебной деятельности и психологических, философских исследований по проблемам мышления позволяет выделить особую роль научных, математических методов познания в совершенствовании мыслительных операций как наиболее способствующих развитию логического мышления студентов. С этой точки зрения реализация современных тенденций общего образования требует изучения любого материала до уровня выявления основных понятий, идей, методов.
Литература:
1. Харламов И.Ф. Педагогика. - М.: Юрист, 1997. - 512 с.
2. Абылкасымова А.Е. Методика преподавания математики.- Алматы, 1998. - 220 c.
3. Маланов С.В. Психологические механизмы мышления человека: мышление в науке и учебной деятельности. – М.: Изд-во Московского психолого-социального института; Воронеж: Издательство НПО «МОДЭК», 2004. – 480 с.
