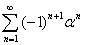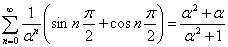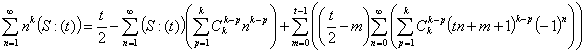В статье представлены формулы и методы нахождения обобщенных сумм знакопеременных рядов, в основном расходящихся, путем преобразования к повторным рядам вложенного типа.
Общий вид повторных рядов вложенного типа: 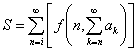
Расходящиеся знакопеременные ряды можно классифицировать по таким трем классам:
1. Ряды с постоянным радиусом обвертывания: 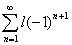
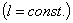
Сумма такого ряда равна 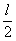 , этот результат достигается многими методами, которые, в силу их известности, демонстрировать в данной статье нет смысла.
, этот результат достигается многими методами, которые, в силу их известности, демонстрировать в данной статье нет смысла.
2. Ряды с ограниченным радиусом обвертывания: 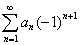 , где
, где 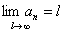
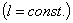
На пример ряд: 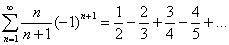 , его обобщенной суммой будет
, его обобщенной суммой будет 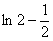
3. Ряды с бесконечным радиусом обвертывания: 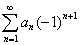 , где
, где 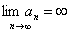
Самым известным таким рядом является: 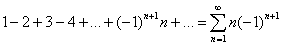
Формула 1: 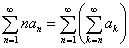
Доказательство: 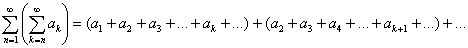
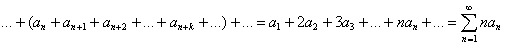
Пусть 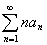 - абсолютно сходящийся ряд. Тогда по известной теореме, если некоторый ряд
- абсолютно сходящийся ряд. Тогда по известной теореме, если некоторый ряд 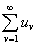 сходится абсолютно, то и любой повторный ряд, составленный из его членов в произвольном порядке, сходится, и притом к той же сумме. И наоборот; абсолютная сходимость повторного ряда ведет за собою абсолютную сходимость одинарного, составленного из его членов и при том к той же сумме.
сходится абсолютно, то и любой повторный ряд, составленный из его членов в произвольном порядке, сходится, и притом к той же сумме. И наоборот; абсолютная сходимость повторного ряда ведет за собою абсолютную сходимость одинарного, составленного из его членов и при том к той же сумме.
Далее, пусть ряд 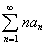 сходится не абсолютно, либо и вовсе расходится. По равенству в доказательстве, любой член ряда
сходится не абсолютно, либо и вовсе расходится. По равенству в доказательстве, любой член ряда 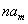 будет полностью просуммирован после начала суммирования
будет полностью просуммирован после начала суммирования 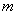 -го ряда в двойном ряде
-го ряда в двойном ряде 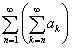 , т. е. ряда
, т. е. ряда 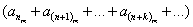 .
.
Тогда каждому возрастанию номера 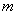 будет отвечать факт следующего полностью просуммированного члена ряда
будет отвечать факт следующего полностью просуммированного члена ряда 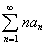
Исходя из этого, ряд, у которого сумма 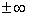 преобразится в ряд с аналогичной суммой:
преобразится в ряд с аналогичной суммой: 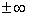 , а знакопеременный ряд с некоторой обобщенной суммой
, а знакопеременный ряд с некоторой обобщенной суммой 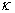 будет преобразован в ряд с такой же суммой. Этим доказательство завершается.
будет преобразован в ряд с такой же суммой. Этим доказательство завершается.
Следствие 1.1: 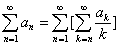
Следствие 1.2: 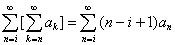
Следствие 1.3: 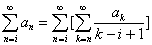
Наглядно, формула 1 представляет собою преобразование ряда 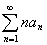 в сумму бесконечного количества рядов
в сумму бесконечного количества рядов 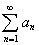 , каждый последующий из которых лишен первого члена в сравнении с предыдущим:
, каждый последующий из которых лишен первого члена в сравнении с предыдущим:
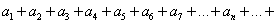
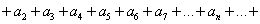
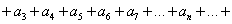
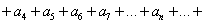

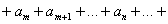
Пусть ряд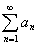 сходится к сумме
сходится к сумме 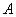 (сумма
(сумма 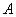 может быть и обобщенной). Тогда нетрудно заметить, что
может быть и обобщенной). Тогда нетрудно заметить, что 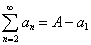 ,
, 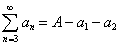 ,…,
,…, 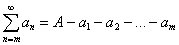 .
.
Самым простым применением формулы 1 может быть суммирование ряда 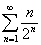 ;
;
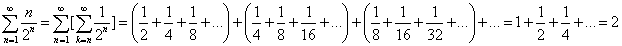
Следующим применением формулы 1 есть суммирование ряда: 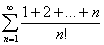
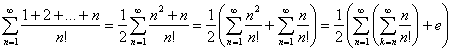
Так как 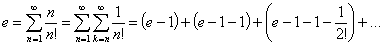 , то
, то
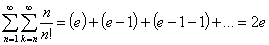
Исходя из этого, 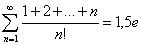
Следует заметить, что хоть формула 1 с ее следствиями, знакопеременный ряд с некоторой обобщенной суммой 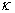 преобразует в ряд с такой же суммой, но радиус обвертывания при этом может и не совпадать. Первым примером того будет суммирование по формуле 1, ряда:
преобразует в ряд с такой же суммой, но радиус обвертывания при этом может и не совпадать. Первым примером того будет суммирование по формуле 1, ряда: 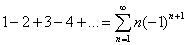
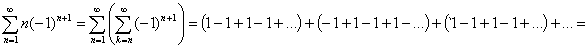
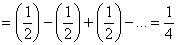
В данном случае для отыскания суммы, ряд с бесконечным радиусом обвертывания был преобразован в ряд, у которого радиус обвертывания есть число постоянное.
Вторым примером может быть ряд 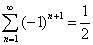 . Применение к нему следствия 1.1, которое является частным случаем формулы 1, дает равенство:
. Применение к нему следствия 1.1, которое является частным случаем формулы 1, дает равенство:
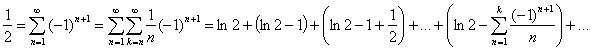
Ряд 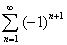 имеет постоянный радиус обвертывания, следственно имеет лишь обобщенную сумму, в то время как ряд в последнем равенстве справа сходится, и соответственно имеет радиус обвертывания равный нулю.
имеет постоянный радиус обвертывания, следственно имеет лишь обобщенную сумму, в то время как ряд в последнем равенстве справа сходится, и соответственно имеет радиус обвертывания равный нулю.
Формула 2: 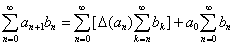 ,
,
где  — разностный оператор:
— разностный оператор: 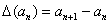 , ряд
, ряд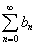 сходится, либо является знакопеременным и имеет обобщенную сумму.
сходится, либо является знакопеременным и имеет обобщенную сумму.
Доказательство: 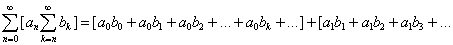
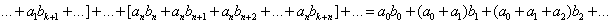
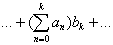
В силу того, что:
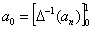
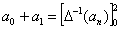

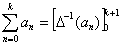
 ,
,
и учитывая, что сумма не зависит от обозначения переменной суммирования:
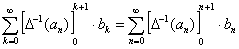 ,
,
изначальную сумму можно представить в виде:
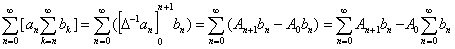 , (1*)
, (1*)
где 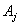 - антиразностный оператор от
- антиразностный оператор от 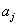 :
: 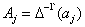
Равенство (1*) может быть представлено в виде:
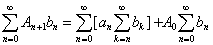 (2*)
(2*)
Равенство (2*) является полностью аналогичным требуемой формуле:
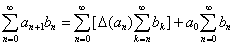
В силу того, что абсолютная сходимость ряда 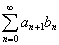 влечет за собой и абсолютную сходимость любого повторного ряда, составленного из его членов в произвольном порядке, и притом к той же сумме; формула 2, в случае абсолютно сходящегося ряда, является оправданной. В противном случае рассуждения аналогичны с доказательством формулы 1, которая является частным случаем формулы 2 при
влечет за собой и абсолютную сходимость любого повторного ряда, составленного из его членов в произвольном порядке, и притом к той же сумме; формула 2, в случае абсолютно сходящегося ряда, является оправданной. В противном случае рассуждения аналогичны с доказательством формулы 1, которая является частным случаем формулы 2 при 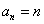 . Этим доказательство и завершается.
. Этим доказательство и завершается.
Обобщением формулы 2 является
Формула 3: 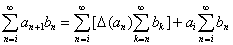
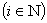
Доказывается аналогично формуле 2.
Формулы: 2 и 3, как и формула 1, действительны и в случае, когда 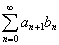 — знакопеременный сходящийся, либо знакопеременный расходящийся ряд с некоторой обобщенной суммой
— знакопеременный сходящийся, либо знакопеременный расходящийся ряд с некоторой обобщенной суммой 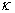 , что будет более детально показано ниже. Если в формулах 2 и 3 за последовательность
, что будет более детально показано ниже. Если в формулах 2 и 3 за последовательность 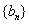 принять последовательность знакопеременного расходящегося ряда первого типа по классификации, а за
принять последовательность знакопеременного расходящегося ряда первого типа по классификации, а за 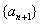 принять оставшуюся часть ряда, то при преобразованиях 2 и 3, знакопеременный расходящийся ряд переходит в знакопеременный расходящийся ряд, а обобщенная сумма не нарушится. Далее будут показаны такие случаи.
принять оставшуюся часть ряда, то при преобразованиях 2 и 3, знакопеременный расходящийся ряд переходит в знакопеременный расходящийся ряд, а обобщенная сумма не нарушится. Далее будут показаны такие случаи.
Формула 4: 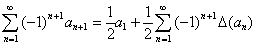
Доказательство: по формуле 3, полагая 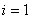 , выходит равенство
, выходит равенство
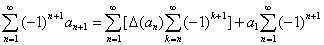 (3*)
(3*)
Так как 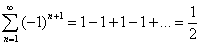 ,
,
то две суммы справа в равенстве (3*) будут соответственно иметь вид:
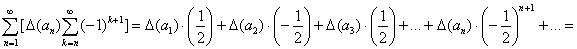
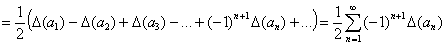
и аналогично: 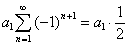
Если подставить оба результата в равенство (3*), то и выйдет требуемая формула
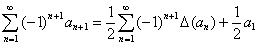
Общая формула 4: 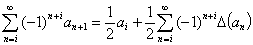
Формула 4, вместе с ее общим вариантом, действительна и в случае сходящегося знакопеременного ряда 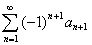 , так как он представляет частный случай знакопеременного ряда, а именно ряда, у которого радиус обвертывания приближается к нулю.
, так как он представляет частный случай знакопеременного ряда, а именно ряда, у которого радиус обвертывания приближается к нулю.
В формуле 4 был использован тот факт, что сумма ряда 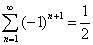 , поэтому она дает нахождение суммы знакопеременного ряда
, поэтому она дает нахождение суммы знакопеременного ряда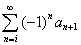 только в ее обобщенном смысле и, не дает никаких сведений о его сходимости или расходимости. Но последнее определяется легко, путем дополнительного анализа.
только в ее обобщенном смысле и, не дает никаких сведений о его сходимости или расходимости. Но последнее определяется легко, путем дополнительного анализа.
При этом ряд, преобразованный по формуле 4 или ее общим вариантом, может оказаться как суммируемым обобщенно, так и сходящимся.
Формула 4 позволяет находить обобщенные суммы некоторых видов:
(В этом пункте и далее 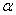 будет произвольным вещественным числом, большим нуля)
будет произвольным вещественным числом, большим нуля)
По формуле 4: 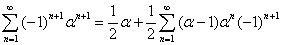
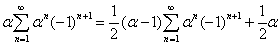
Если положить: 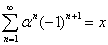 , то выйдет легко разрешимое уравнение
, то выйдет легко разрешимое уравнение
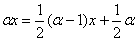 , его решением будет:
, его решением будет: 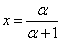
Возвращение к подстановке приводит к окончательному результату:
Формула 4.1: 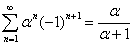
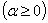
Следствие 4.1.1: 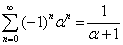
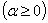
Данное следствие примечательно тем, что служит доказательством равенства 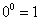 .
.
Выводится достаточно просто: 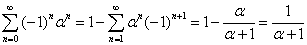
Отсюда, в частности, выходит обобщенная сумма хорошо известного расходящегося ряда
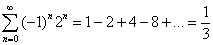
Дальнейшие два следствия формулы 4.1 выводятся заменой 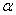 на
на 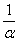
Следствие 4.1.2: 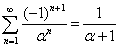
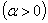
Следствие 4.1.3: 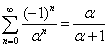
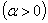
Оба последних следствия при 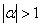 представляют собой формулы нахождения сумм абсолютно сходящихся знакопеременных рядов.
представляют собой формулы нахождения сумм абсолютно сходящихся знакопеременных рядов.
4.2 Нахождение обобщенной суммы: 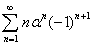
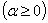
Действия аналогичны; по формуле 4 для данного ряда будет справедливо равенство:
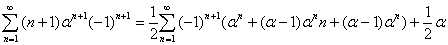
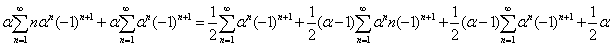
Полагая 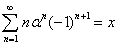 , и учитывая что
, и учитывая что 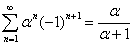 , выходит уравнение:
, выходит уравнение:
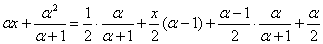
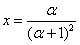 , из чего следует
, из чего следует
Формула 4.2: 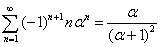
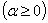
Следствие 4.2.1: 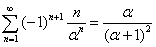
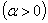
4.3 Нахождение обобщенной суммы: 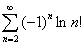
Очевидно, что 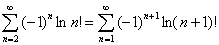 , т. е. отсчет суммирования может быть начат с единицы.
, т. е. отсчет суммирования может быть начат с единицы.
Применив формулу 4, переводя для удобства отсчет суммы с единицы, выходит
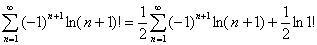
Второе слагаемое справа равно нулю, а первая сумма справа выводится из известной формулы: 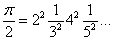
При логарифмировании обеих частей последнего равенства выходит результат:
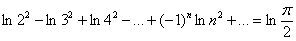 ,
,
или
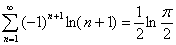 ;
;
тогда искомая сумма будет представлена следующей формулой:
Формула 4.3: 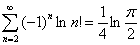
Данный результат может быть также представлен в виде: 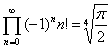
4.4 Нахождение обобщенной суммы: 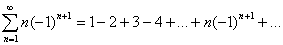
Применяя формулу 4, 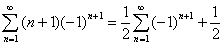
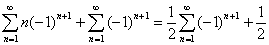
Как известно, 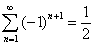 , из чего следует:
, из чего следует:
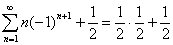
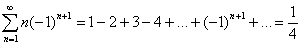
4.5 Общая рекуррентная формула нахождения сумм вида: 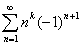 ,
,
где 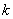 - натуральное число.
- натуральное число.
Формула 4.5: 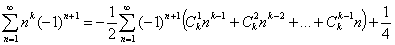
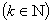
Эта формула может быть представлена в таких видах:
— 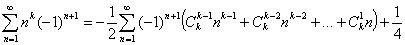
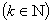
— 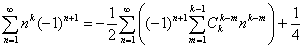
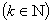
— 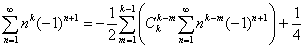
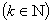
Последний вариант наиболее пригоден к вычислению.
Доказательство формулы 4.5: По формуле 4, будет справедливым равенство:
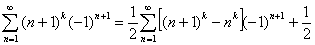 ,
,
из чего следует:
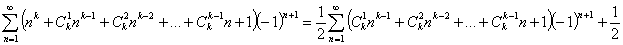
При раскрытии скобок во всем равенстве и переносе из левой части равенства все слагаемые в правую, кроме 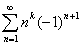 , выходит:
, выходит:
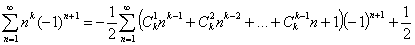
Исходя из того, что 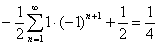 , последнее равенство может быть окончательно представлено в виде требуемой формулы:
, последнее равенство может быть окончательно представлено в виде требуемой формулы:
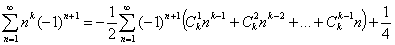
Этим доказательство и завершается.
С помощью рекуррентной формулы 4.5 легко вычислить обобщенные суммы следующих известных расходящихся рядов:
4.5.1: 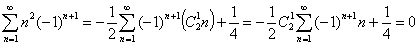
4.5.2: 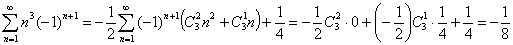
4.5.3: 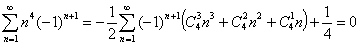
4.5.4: 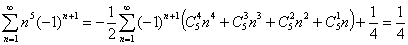
4.6 Рекуррентная формула для обобщенной суммы вида: 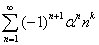
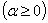
Формула 4.6: 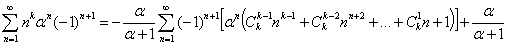
Доказательство:
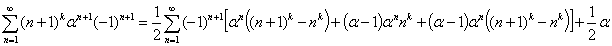
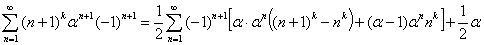
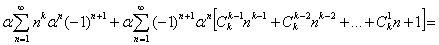
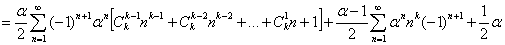
Если положить:
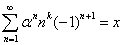
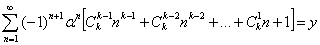 ,
,
то выйдет уравнение: 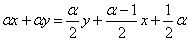 , решение которого:
, решение которого: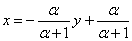
Возвращая 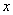 и
и 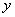 их ранее подставленные значения, легко прийти к окончательной формуле.
их ранее подставленные значения, легко прийти к окончательной формуле.
Ранее было показано, что 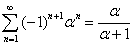
С помощью последней выведенной рекуррентной формулы можно получить уже ранее выведенный результат:
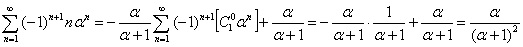
Формула 5: 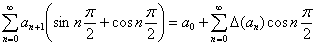
Доказательство: Сначала следует доказать, что ряд:
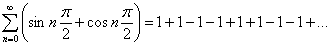 , имеет обобщенной суммой число
, имеет обобщенной суммой число 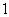 .
.
Методом средних арифметических легко выводиться известная формула: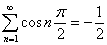
Тогда: 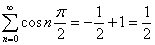
Аналогично, тем же методом выводится известная формула: 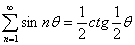
Пусть 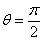 , тогда
, тогда 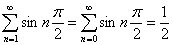
Стало быть,
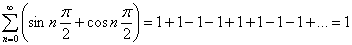 (4*)
(4*)
Тогда по формуле 2:
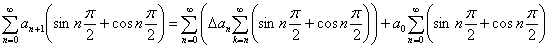 (5*)
(5*)
Так как 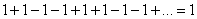 , то
, то
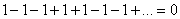
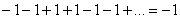
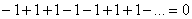 ,
,
и тогда все 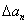 с непарными номерами
с непарными номерами 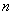 , в первой из сумм справа в равенстве (5*) будут произведены на
, в первой из сумм справа в равенстве (5*) будут произведены на 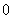 , следовательно равняться нулю.
, следовательно равняться нулю.
Второе слагаемое справа, в равенстве (5*), ввиду равенства (4*), будет равно 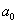
Исходя из этого, равенство (5*) примет вид:
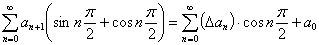 , что и требовалось доказать.
, что и требовалось доказать.
Формула 5 так же имеет множество применений:
Выводится просто; по формуле 5:
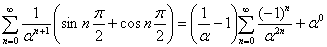 (6*)
(6*)
Ранее уже была выведена формула: 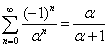 , для всех вещественных
, для всех вещественных 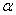
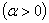 .
.
Если в ней положить 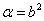 , то правильность данной формулы при этом не изменится.
, то правильность данной формулы при этом не изменится.
И тогда сумма 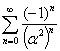 будет равна
будет равна 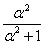 ,
,
Это дает возможность равенство (9*) представить в виде
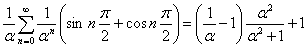 ,
,
а затем, путем элементарных преобразований получить окончательный результат.
Формула 5.1 может быть представлена более наглядно в виде:
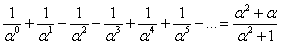
5.2 Нахождение обобщенной суммы вида:
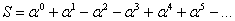
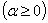
Формула 5.2: 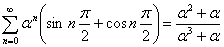
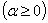
Выводится аналогично; по формуле 5:
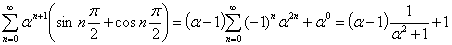
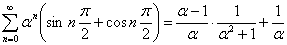
После элементарных преобразований легко получить требуемую формулу.
5.3 Нахождение обобщенной суммы ряда:
По формуле 5: 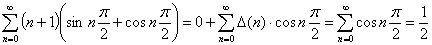
Обобщенная формула 5:
Ее доказательство аналогично формуле 5, отличие лишь в том, что за основу берется формула 3.
5.4 Частный вид обобщенной формулы 5
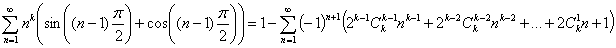
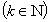
Данная формула выводится подобно предыдущим:
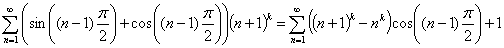
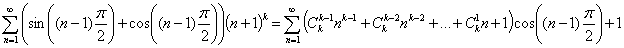 Разложение аналогичным образом по степеням множителя
Разложение аналогичным образом по степеням множителя 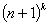 в последнем равенстве, в выражении слева, дает возможность сократить обе части равенства на слагаемое:
в последнем равенстве, в выражении слева, дает возможность сократить обе части равенства на слагаемое:
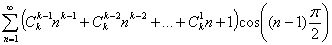
Тогда, после перегруппировки, последнее равенство будет иметь вид:
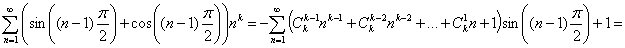
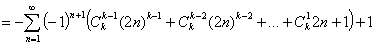
Из этой формулы, в частности, при 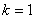 , и выходит ранее полученный результат:
, и выходит ранее полученный результат:
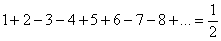
При 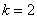 :
: 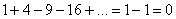
Формула 5.5: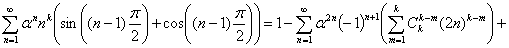
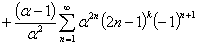
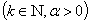
Выводится аналогично предыдущим случаям из обобщения формулы 5:
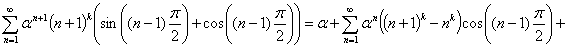
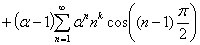
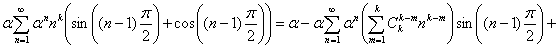
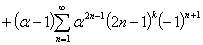
В силу равенства: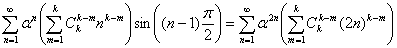 , легко прийти к требуемой формуле.
, легко прийти к требуемой формуле.
К примеру, 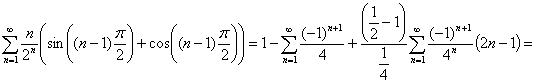

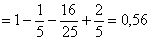
Формула 6 (общая рекуррентная формула суммирования расходящихся рядов):
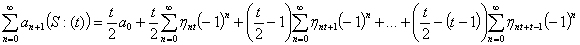 ,
,
где 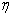 — уже вычисленная разность от
— уже вычисленная разность от 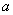 :
: 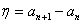 ,
,
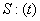 - такой множитель, что при суммировании некоторого ряда
- такой множитель, что при суммировании некоторого ряда 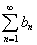 , его суммирование происходит следующим образом: первая частичная сумма
, его суммирование происходит следующим образом: первая частичная сумма 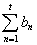 положительна, вторая частичная сумма:
положительна, вторая частичная сумма: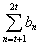 отрицательна, третья:
отрицательна, третья: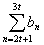 положительна и т. д.
положительна и т. д.
Выводится эта формула подобно формулам 4 и 5 на основе тех же соображений.
Так как обобщенная сумма ряда: 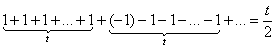 , что может быть легко доказано методом средних арифметических, то формула 2 может быть применена и на этот более общий случай.
, что может быть легко доказано методом средних арифметических, то формула 2 может быть применена и на этот более общий случай.
Более краткая интерпретация формулы 6 имеет вид:
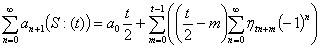
Очевидно, при 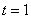 и
и 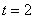 из этой формулы следуют формула 4 и формула 5 соответственно.
из этой формулы следуют формула 4 и формула 5 соответственно.
К примеру, пусть требуется просуммировать ряд: 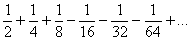
В данном случае, в операторе 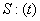 , будет
, будет 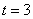 , так как первые три члена положительны, далее идут три члена с отрицательным знаком, далее три с положительным и т. д.
, так как первые три члена положительны, далее идут три члена с отрицательным знаком, далее три с положительным и т. д.
Разность вычисляется легко: 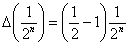 , тогда по общей формуле:
, тогда по общей формуле:
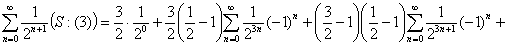
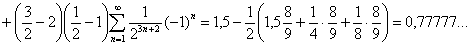
Более общий вариант формулы 6:
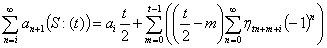
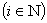
Его частные случаи будут иметь вид:
2.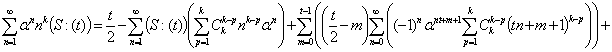
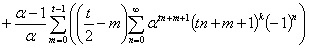
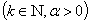
3.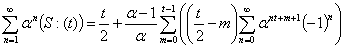
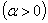
Из первой формулы, в частности, при 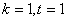 выходит результат
выходит результат 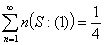 ,
,
а именно: 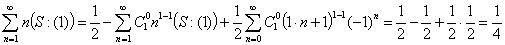
Первые две формулы можно представить в более удобным для вычисления виде:
1. 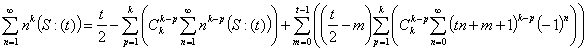
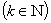
2.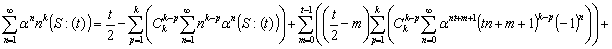
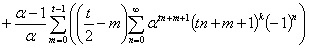
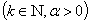
Этими тремя формулами вопрос о суммировании расходящихся рядов трех видов:
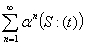 ,
,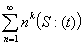 ,
,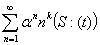 исчерпывается полностью.
исчерпывается полностью.