Рассмотрим кинетический процесс, протекающий в гомогенной системе с постоянными или с непрерывно изменяющимися химическим составом и физическими свойствами (между частями системы нет поверхностей раздела). Если стабилизированное, эксплуатационное значение 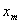 рассматриваемой характеристики
рассматриваемой характеристики 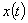 изменить за счет внешнего возмущающего воздействия, а затем снять это возмущение, то параметр
изменить за счет внешнего возмущающего воздействия, а затем снять это возмущение, то параметр 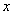 вернется к значению
вернется к значению 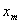 . Так что:
. Так что:
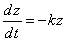 ,
,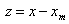 .
.
При начальных условиях 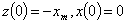 получим
получим
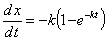
(предполагается, что проявление отдельных структурных элементов либо подавлено глобальными процессами, либо влияние этих процессов на систему незначительно). Такое предположение практически неприемлемо для дисперсных систем, к которым относятся и композитные материалы [1…3]. Для них характерно наличие точки перегиба функции 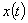 , определяющей исследуемый процесс (в гомогенных системах точки перегиба нет).
, определяющей исследуемый процесс (в гомогенных системах точки перегиба нет).
В отклонениях от равновесного состояния 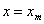 будем иметь
будем иметь
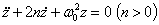 .
.
Пусть 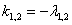 — корни характеристического полинома.
— корни характеристического полинома.
При 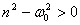 имеем
имеем 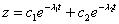 ,
,
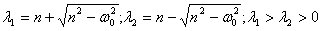 .
.
При 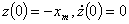 имеем
имеем
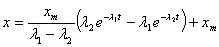 .
.
Из 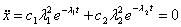 получим координату точки перегиба
получим координату точки перегиба
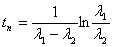 . (1)
. (1)
(при вогнутость сменяется на выпуклость).
Так как l2 < l1, то составляющая 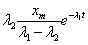 затухает быстрее, чем аналогичная составляющая
затухает быстрее, чем аналогичная составляющая 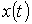 , соответствующая корню l2. Поэтому значение l2 можно определить по концу экспериментально полученного процесса
, соответствующая корню l2. Поэтому значение l2 можно определить по концу экспериментально полученного процесса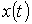 .
.
Без ограничения общности рассуждений можно принять 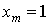 (равносильно масштабированию
(равносильно масштабированию 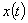 ).
).
При 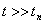
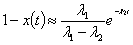 =
=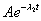 .
.
Откуда
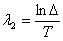 ,
, 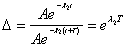 .
.
Из 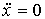 получим
получим
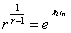 ;
; 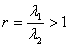 .
.
Полученное уравнение имеет решение 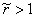 лишь при
лишь при 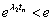 .
.
Откуда
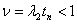 ;
; 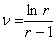 ,
, 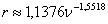 .
.
Из 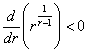 при
при 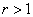 и
и 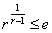 в интервале (1,
в интервале (1, 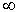 ) следует
) следует 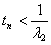 .
.
Изменение структуры, физико-механических и эксплуатационных свойств материала приводят к изменению
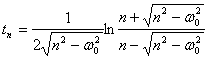
(w0 определяет упругость системы, а n — рассеяние (демпфирование) энергии). С ростом 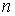 и
и 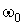 (
(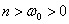 ,
, 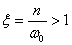 ) значение
) значение 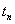 убывает.
убывает.
При 
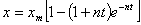 ,
,
в частности, при 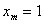
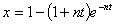 .
.
Точка перегиба процесса 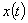 есть точка
есть точка 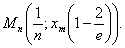
Увеличение 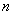 ведет к уменьшению
ведет к уменьшению 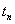 , то есть сдвигу точки
, то есть сдвигу точки 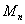 влево.
влево.
При n> 1 точка 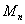 лежит левее прямой
лежит левее прямой 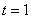 , а при n< 1 — правее.
, а при n< 1 — правее.
Время t0 выхода контролируемого параметра на эксплуатационное значение 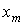 определится из условия
определится из условия
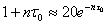 .
.
Рассмотрим кинетические процессы видов, приведенных на рис. 1.

Рис. 1
Кривая 1 характерна для кинетики внутренних напряжений в эпоксидных композитах. Здесь кинетический процесс описывается в виде:
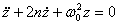
и является решением уравнения при начальных условиях
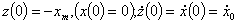 .
.
Таким образом, указанные процессы имеют вид
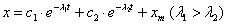 .
.
Для точки перегиба 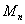 абсцисса
абсцисса
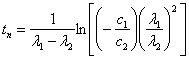 , (2)
, (2)
где постоянные интегрирования определяются из условий:
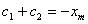 ,
,
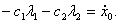
Абсцисса точки 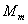 должна удовлетворять условию
должна удовлетворять условию 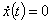 , что дает:
, что дает:
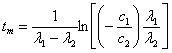 . (3)
. (3)
Должны иметь
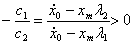
Откуда следует, что 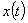 достигает максимума при
достигает максимума при 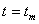 и при выполнении одного из условий
и при выполнении одного из условий 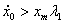 или
или  .
.
Имеем
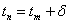 ,
,
где
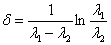 .
.
Из изложенного выше вытекает следующий алгоритм идентификации кинетических процессов рассматриваемого вида:
- по концу переходного процесса определяется l2;
- определяется 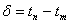 ;
;
- по известным l2 и d определяется l1;
- по при известных l1 и l2 определяется 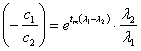 ;
;
- по известным значениям 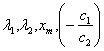 определяется
определяется
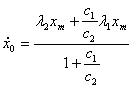 .
.
Наконец, определяется
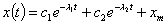 .
.
Задача идентификации решена полностью. Настройка модели легко осуществляется с учетом влияния идентифицируемых параметров на характеристики кинетических процессов.
Как показывает практика, существуют системы, кинетические процессы в которых не могут быть описаны рассмотренными выше моделями первого и второго порядка. К таким системам, в частности, относятся некоторые полидисперсные системы. Так, например, кинетика набора прочности композиционного материала имеет иногда не одну, а две точки перегиба. Пути обобщения приведенных выше методик для идентификации таких кинетических процессов очевидны [4,5].
Литература:
1. Будылина Е. А., Гарькина И. А. Данилов А. М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. № 2(16). 2013. — C. 138–143.
2. Гарькина И. А., Данилов А. М. Управление в сложных технических системах: методологические принципы проектирования системах / Региональная архитектура и строительство. № 1. 2012. — C. 39–42.
3. Будылина Е. А., Гарькина И. А., Данилов А. М., Сухов Я. И. Некоторые подходы к анализу и синтезу сложных систем / «Молодой ученый. — № 10(57), 2013. — с.105–107.
4. Гарькина И. А., Данилов А. М., Петренко В. О. Проблема многокритериальности при управлении качеством сложных систем / Мир транспорта и технологических машин. № 2(41). 2013. –С.123–130.
5. Данилов А. М., Гарькина И. А. Методология проектирования сложных систем при разработке материалов специального назначения / Известия ВУЗов. Строительство. — 2011. -№ 1.-С.80–85.







