Работа посвящена распространению результатов исследований сильных средних отклонений операторов Фурье на случай, когда в качестве агрегатов приближения выступают операторы Валле Пуссена.
1. В теории рядов Фурье хорошо известно, что 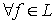 почти всюду на
почти всюду на 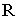 выполняется соотношение
выполняется соотношение 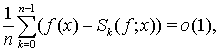 где
где 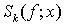 — частные суммы Фурье функции
— частные суммы Фурье функции 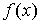 ,
, 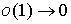 при
при 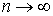 .
.
Харди и Литтлвуд поставили вопрос: будет ли 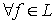 выполняться более общее соотношение
выполняться более общее соотношение
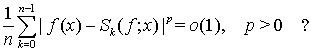 (1)
(1)
Если соотношение (1) выполнено, то говорят, что ряд Фурье функции 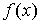 является сильно суммируемым с показателем
является сильно суммируемым с показателем 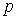 .
.
Исследованию сформулированого вопроса для сумм и операторов Фурье на классах 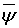 -интегралов периодических функций и классах
-интегралов периодических функций и классах 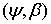 -производных локально интегрируемых функций были посвящены работы [1, 2].
-производных локально интегрируемых функций были посвящены работы [1, 2].
Мы обобщим эти исследования на случай классов 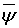 -интегралов локально интегрируемых функций когда аппаратом аппроксимации выступают операторы Валле Пуссена.
-интегралов локально интегрируемых функций когда аппаратом аппроксимации выступают операторы Валле Пуссена.
Сначала приведем определение классов Степанца (см. [3]).
Обозначим через 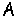 множество непрерывных при
множество непрерывных при 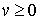 функций
функций 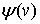 , которые удовлетворяют условия: 1)
, которые удовлетворяют условия: 1) 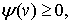
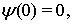
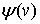 возрастает на
возрастает на 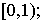 2)
2) 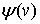 выпукла вниз на
выпукла вниз на 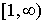 и
и 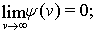 3) производная
3) производная 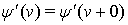 имеет ограниченную вариацию на
имеет ограниченную вариацию на 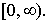 Подмножество функций
Подмножество функций 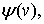 для которых
для которых 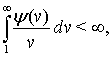 обозначают
обозначают 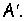 Множество функций
Множество функций 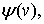 которые удовлетворяют лишь условию 2) обозначают
которые удовлетворяют лишь условию 2) обозначают 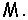
Для пары 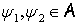 определим функцию
определим функцию 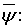
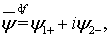 где
где 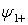 и
и 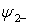 — четное и нечетное продолжения функций
— четное и нечетное продолжения функций 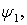
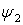 соответственно.
соответственно.
Пусть 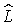 — множество функций
— множество функций 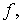 которые определены на действительной оси и имеют конечную норму
которые определены на действительной оси и имеют конечную норму 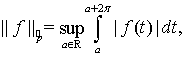
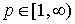 ,
, 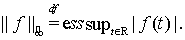 Тогда через
Тогда через 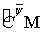 будем обозначать подмножество непрерывных функций
будем обозначать подмножество непрерывных функций 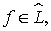 которые для всех
которые для всех 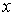 можно представить в виде следующего равенства:
можно представить в виде следующего равенства:
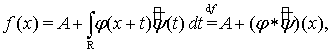 (2)
(2)
где 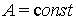 , интеграл понимаем как границу по симметричным расширяющимся промежуткам,
, интеграл понимаем как границу по симметричным расширяющимся промежуткам, 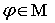 , т. е.,
, т. е., 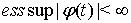 ,
,
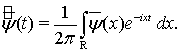 (3)
(3)
Если 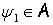 ,
, 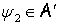 , то преобразование
, то преобразование 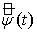 суммируемо на действительной оси (см., например, [4]).
суммируемо на действительной оси (см., например, [4]).
Следуя А. И. Степанцу [5], функцию 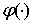 в изображении (2) называют
в изображении (2) называют 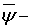 производной функции
производной функции 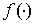 и обозначают
и обозначают 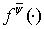 .
.
Для приближения функций из классов 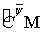 будем использовать операторы Валле Пуссена
будем использовать операторы Валле Пуссена
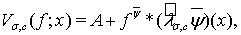 (4)
(4)
где 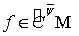 , а
, а 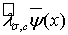 преобразование вида (3) функции
преобразование вида (3) функции 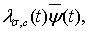 в которой
в которой
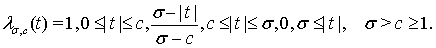 (5)
(5)
Такие операторы рассматривались А. И. Степанцом в работах [3, 4, 6], где показано, что при определенных условиях 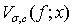 принадлежат к множеству
принадлежат к множеству 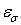 целых функций экспоненциального типа
целых функций экспоненциального типа 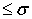 , а в периодическом случае, при натуральных
, а в периодическом случае, при натуральных 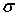 и
и 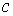 операторы
операторы 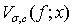 совпадают с суммами Валле Пуссена.
совпадают с суммами Валле Пуссена.
Далее, следуя [4], из множества 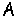 выделим подмножества
выделим подмножества 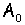 и
и 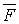 . Каждой функции
. Каждой функции 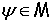
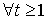 сопоставим пару функций
сопоставим пару функций 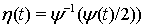 и
и 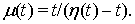
Тогда: 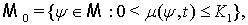
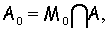
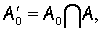
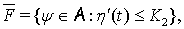 где
где 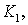
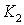 — некоторые постоянные, которые, возможно, зависят от функции
— некоторые постоянные, которые, возможно, зависят от функции 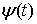 .
.
Аппроксимативные свойства операторов Валле Пуссена в нашей работе характеризуются функционалами
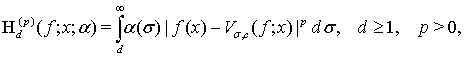
в которых 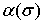 — некоторая неотрицательная непрерывная при всех
— некоторая неотрицательная непрерывная при всех 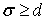 функция.
функция.
Положим: 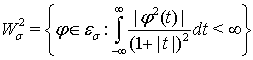 ;
; 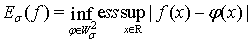 ;
; 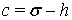 и
и 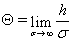 .
.
В принятых обозначениях имеют место утверждения.
Теорема 1.Пусть 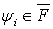 ,
, 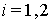 и такие,что найдутся константы
и такие,что найдутся константы 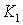 и
и 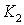 для которых выполняется условие
для которых выполняется условие
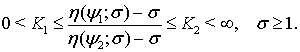 (6)
(6)
Числа 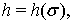 удовлетворяют условию:
удовлетворяют условию: 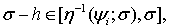
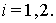 Пусть, далее,
Пусть, далее, 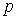 — произвольное положительное число и функция
— произвольное положительное число и функция 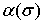 такова, что произведение
такова, что произведение 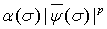 не возрастает
не возрастает
Тогда, если 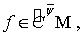 то для произвольных
то для произвольных 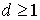 выполняется неравенство
выполняется неравенство
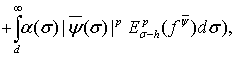 (7)
(7)
в котором 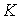 — величина, не зависящая от
— величина, не зависящая от 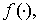
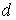 и
и 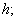 в качестве величины
в качестве величины 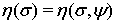 может выступать любая из функций
может выступать любая из функций 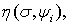
Теорема 2.Пусть 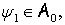
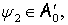 числа
числа 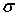 и
и 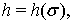
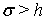 выбраны так, что
выбраны так, что 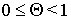 ,
, 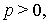 а функция
а функция 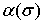 такова, что произведение
такова, что произведение 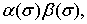 где
где 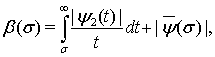 не возрастает
не возрастает
Тогда, если 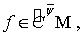 то для произвольных
то для произвольных 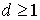 выполняется неравенство
выполняется неравенство
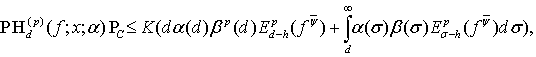 (8)
(8)
в котором 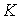 — величина не зависящая от
— величина не зависящая от 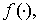
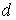 и
и
Замечание. В случае 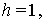
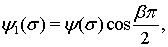
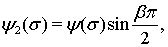
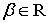 и
и 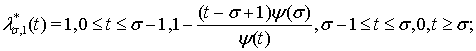
 (т. е., для классов
(т. е., для классов 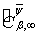 ) теоремы 1 и 2 получены А. И. Степанцом и Н. Л. Пачулиа [2]. Заметим, что в аналоге теоремы 2 рассматривается лишь случай
) теоремы 1 и 2 получены А. И. Степанцом и Н. Л. Пачулиа [2]. Заметим, что в аналоге теоремы 2 рассматривается лишь случай 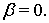 Для сумм Фурье в периодическом случае аналогичная задача была решена А. И. Степанцом.
Для сумм Фурье в периодическом случае аналогичная задача была решена А. И. Степанцом.
2. Доказательство теорем начнем с получения некоторых вспомогательных утверждений. Пусть 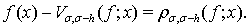 Величину
Величину 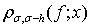 рассмотрим в двух частных случаях, в зависимости от скорости следования к нулю пары функций
рассмотрим в двух частных случаях, в зависимости от скорости следования к нулю пары функций 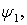
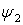 .
.
Лемма 1.Пусть 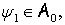
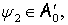 числа
числа 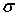 и
и 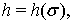
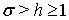 выбраны так, что
выбраны так, что 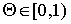 , постоянная
, постоянная 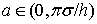 .Тогда
.Тогда 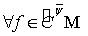 в каждой точке
в каждой точке
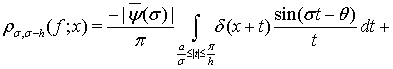
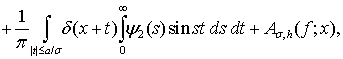 (9)
(9)
где 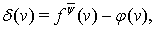
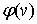 — функция из множества
— функция из множества 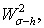 для которой
для которой 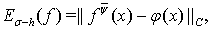
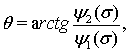
Лемма 2.Пусть 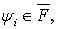
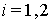 и выполнено условие (6), числа
и выполнено условие (6), числа 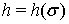 такие, что
такие, что 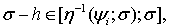
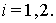 Функции
Функции 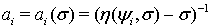 ,
,
Тогда, если 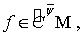 то
то 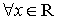 и действительных чисел
и действительных чисел
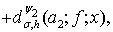 (10)
(10)
где 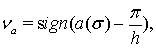
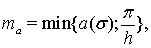
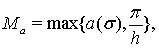 в роли функции
в роли функции 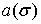 может выступать любая из функций
может выступать любая из функций 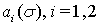 ,
, 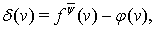
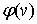 — функция из
— функция из 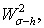 для которой
для которой 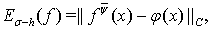
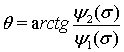 , и
, и 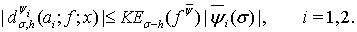 (11)
(11)
3. Пусть 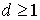 и
и 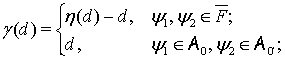
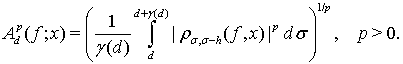 (12)
(12)
Следующим шагом в доказательстве теорем 1 и 2 будет такое утверждение.
Лемма 3.Пусть 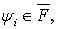
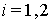 и выполнено условие (6), числа
и выполнено условие (6), числа 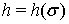 выбираются так, что
выбираются так, что 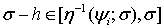 ,
, 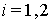 .
.
Тогда, если 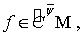 то для любых
то для любых 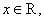
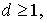
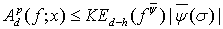 (13)
(13)
Если же 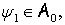
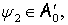 числа
числа 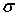 и
и 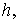
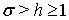 избраны так, что
избраны так, что 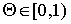 , постоянная
, постоянная 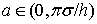 , то
, то 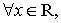
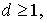
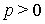 и
и
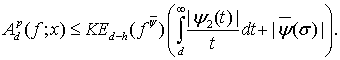 (14)
(14)
В соотношениях (13) и (14) 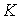 — величина, которая равномерно ограничена по
— величина, которая равномерно ограничена по 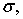
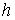 и
и 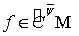 .
.
Доказательство. Из неравенства Гельдера следует, что величина 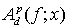 не убывает по параметру
не убывает по параметру 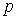 , поэтому неравенства (13) и (14) достаточно доказать лишь при
, поэтому неравенства (13) и (14) достаточно доказать лишь при 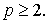 Сначала докажем неравенство (13).
Сначала докажем неравенство (13).
Используя равенство (10) и неравенство Минковского, получим
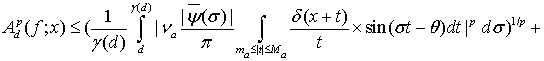
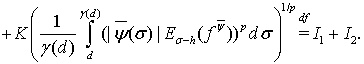 (15)
(15)
Поскольку функция 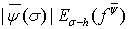 не возрастает, то
не возрастает, то
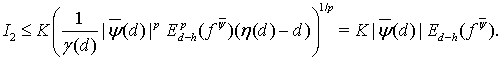 (16)
(16)
Перейдем к получению оценки величины 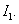 Отметим, что
Отметим, что
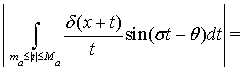
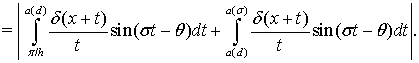
Применяя неравенство Минковского, получим
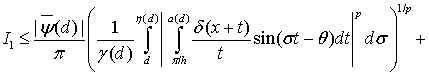
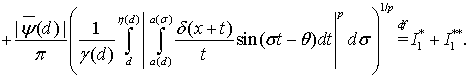 (17)
(17)
Далее,
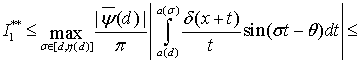
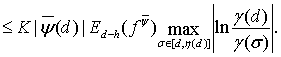
Поскольку, как было установлено в работе [8, с. 239] (соотношение (14.21)),
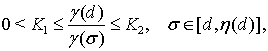 (18)
(18)
то
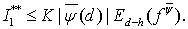 (19)
(19)
Для оценки интеграла 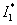 применим неравенство Хаусдорфа-Юнга:
применим неравенство Хаусдорфа-Юнга:
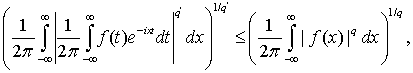
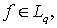
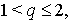
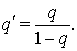
С этой целью положим 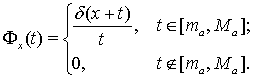
Тогда
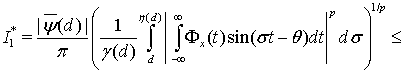
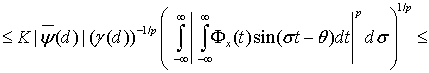
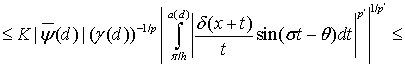
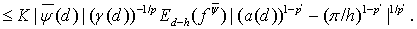
Поскольку 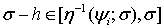 , то
, то
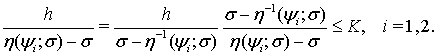 (20)
(20)
А потому 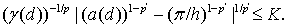
Итак,
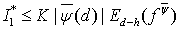 (21)
(21)
Сравнивая соотношения (12) и (15) — (21) приходим к оценке (13).
Перейдем к доказательству неравенства (14).
Используя соотношение (9) из леммы 1 и неравенство Минковского, согласно равенства (12), получим
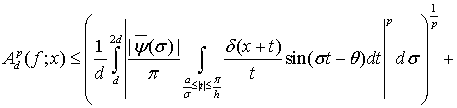
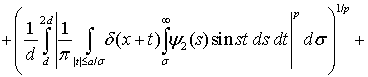
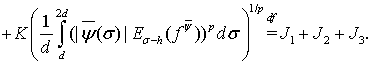 (22)
(22)
Поскольку функция 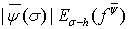 не возрастает, то
не возрастает, то
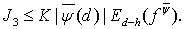 (23)
(23)
Далее мы воспользуемся соотношением (5.5.4) из работы [7, с. 236], при доказательстве которого периодичность функции 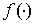 и включение
и включение 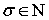 не использовались, а потому
не использовались, а потому
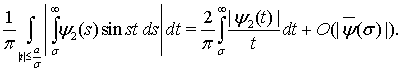 (24)
(24)
Принимая во внимание соотношения (24), имеем
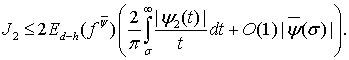 (25)
(25)
Остается установить аналогичную оценку и для интеграла 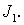
При каждых фиксированных 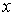 и
и 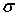 положим
положим
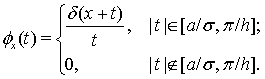
Применяя неравенство Хаусдорфа-Юнга получим
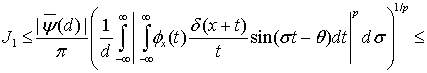
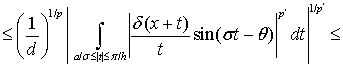
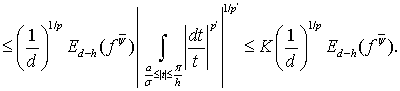 (26)
(26)
При нахождении этого неравенства мы воспользовались также условием 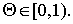 Из соотношений (22) — (23) и (25) — (26) следует неравенство (14).
Из соотношений (22) — (23) и (25) — (26) следует неравенство (14).
Лемма 4 окончательно доказана.
4. Перейдем непосредственно к доказательству теоремы 1.
Пусть 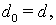
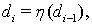
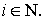 Тогда
Тогда
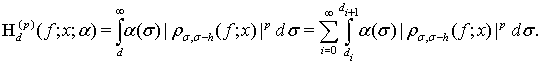
Выберем числа 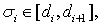
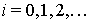 исходя из условия
исходя из условия 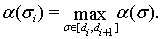
Согласно лемме 3, имеем
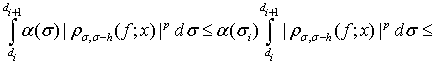
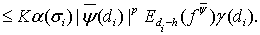
Поэтому
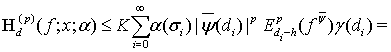
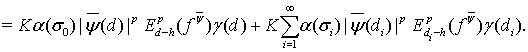 (27)
(27)
Поскольку 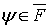 , то, на основании оценки (18),
, то, на основании оценки (18), 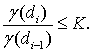 Следовательно
Следовательно
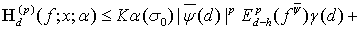
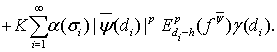 (28)
(28)
Функция 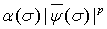 не возрастает и
не возрастает и 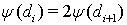 . Соответственно,
. Соответственно, 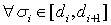
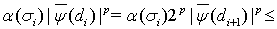
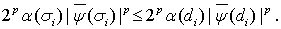
Поэтому, опираясь на соотношение (28), получаем искомую оценку:
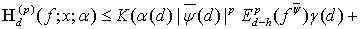
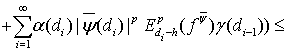
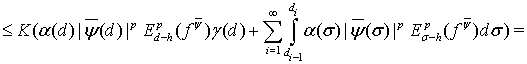
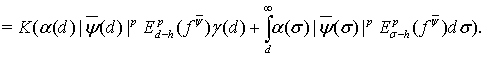 (29)
(29)
Теорема 1 доказана.
5. Доказательство теоремы 2.
Пусть 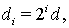
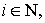 тогда, согласно лемме 1,
тогда, согласно лемме 1,
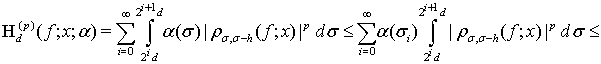
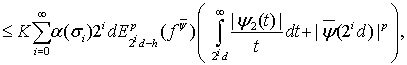 (30)
(30)
где 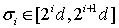 и такие, что
и такие, что 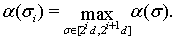
В монографии [7, с. 391] для натуральных значений 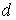 получена оценка
получена оценка
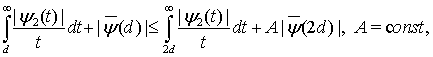 (31)
(31)
которая остается верной и в нашем случае 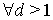 , поскольку при ее доказательстве не использовался тот факт, что
, поскольку при ее доказательстве не использовался тот факт, что 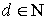 .
.
Обозначим: 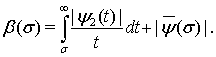 Согласно условию, числа
Согласно условию, числа 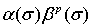 не возрастают. Поэтому, учитывая (31), получим
не возрастают. Поэтому, учитывая (31), получим
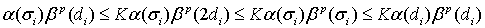
Применяя эту оценку к неравенству (30), находим
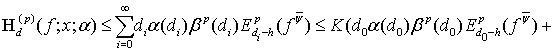
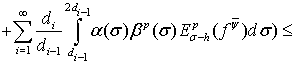
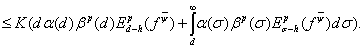
Таким образом, теорема 2 окончательно доказана.
Литература:
1. Степанец А. И. Скорость сходимости группы отклонений на множествах 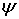 -интегралов // Укр. мат. журн. — 1999. — 51, № 12. — С. 1673–1693.
-интегралов // Укр. мат. журн. — 1999. — 51, № 12. — С. 1673–1693.
2. Степанец А. И., Пачулиа Н. Л. Сильные средние уклонения операторов Фурье // Укр. мат. журн. — 1990. — 42, № 9. — С. 1225–1231.
3. Stepanets A. I., Wang Kunyang, Zhang Xirong. Approximation of locally integrable function on the real line // Укр. мат. журн. — 1999. — 51, № 11. — С. 1549–1561.
4. Степанец А. И. Приближение в пространствах локально интегрируемых функций // Укр. мат. журн. — 1994. — 46, № 5. — С. 597–625.
5. Степанец А. И. Приближение 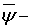 интегралов периодических функций суммами Фурье. — Киев, 1996. — 70 с. — (Препринт / АН Украины. Ин-т математики; 96.11).
интегралов периодических функций суммами Фурье. — Киев, 1996. — 70 с. — (Препринт / АН Украины. Ин-т математики; 96.11).
6. Степанец А. И. Приближение операторами Фурье функций, заданных на действительной оси // Укр. мат. журн. — 1988. — 40, № 2. — С. 198–209.
7. Степанец А. И. Методы теории приближений: В 2 т. — Киев: Ин-т математики НАН Украины, 2002. — Т.1. — 426 с.
8. Степанец А. И. Методы теории приближений: В 2 т. — Киев: Ин-т математики НАН Украины, 2002. — Т.2. — 468 с.







